三角学/仰角和俯角

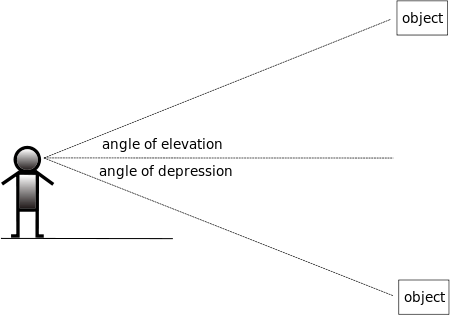
假设您是一位观察者，位于 $O$ ，有一个物体 $Q$ ，不在同一个水平面上。设 $OP$ 是一条水平线，使得 $O,P,Q$ 在一个垂直平面上。那么，如果 $Q$ 在 $0$ 上方，则角度 $\angle QOP$ 是从 $P$ 观察到的 $Q$ 的 **仰角** ，如果 $Q$ 在 $O$ 下方，则角度 $\angle QOP$ 是 **俯角** 。

在使用仰角和俯角时，我们通常忽略人的高度，而是从某个方便的“地面”水平测量角度。

练习 1：对边、斜边、邻边 看上面的图。 $\angle MLT$ 是直角。您将如何用英语翻译这些标签？

示例 1：旗杆 从旗杆底部 $10m$ 处，旗杆顶部的仰角为 $50^{\circ }$ 。求旗杆的高度。 [图] 如果高度是 $h$ ，那么 ${\frac {h}{10}}=\tan(50^{\circ })$ 。因此 $h=10\tan(50^{\circ })=11.92m$ （保留两位小数）。

示例 2：一个 $15m$ 高的旗杆 已知一个旗杆高 $15m$ 。从什么距离观察，它的顶部的仰角为 $50^{\circ }$ ？ [图] 如果距离是$d$，那么${\frac {15}{d}}=\tan(50^{\circ })$。因此$d={\frac {15}{\tan(50^{\circ })}}=12.59m$（保留两位小数）。

例 3：一座$20m$高的塔 从一座高$20m$的塔的底部，旗杆顶部的仰角为$30^{\circ }$。从塔顶看，旗杆顶部的俯角为$25^{\circ }$。求旗杆的高度和它到塔的距离。 设旗杆的高度为h，距离为d。则 (i) ${\frac {h}{d}}=\tan(30^{\circ })$ 由于从塔顶看，旗杆顶部的俯角，所以旗杆顶点在塔顶下方。它比塔顶低$20-h$米，所以 (ii) ${\frac {20-h}{d}}=\tan(25^{\circ })$ 将这两个等式相加，我们得到 (iii) ${\frac {20}{d}}=\tan(30^{\circ })+\tan(25^{\circ })$ 由此（如何？）我们可以得到$d=19.16m\ ,\ h=11.06m$（均保留两位小数）。

例 4：另一个旗杆 从某一点，旗杆顶部的仰角为$30^{\circ }$。沿着直线方向朝旗杆移动$10m$。现在旗杆顶部的仰角为$50^{\circ }$。求旗杆的高度和它到第二点的距离。 [图] 设高度为$h$，它到第二点的距离为$x$。则 $\cot(50^{\circ })={\frac {x}{h}}\ ;\ \cot(30^{\circ })={\frac {x+10}{h}}$ 从第二个表达式中减去第一个表达式， $\cot(30^{\circ })-\cot(50^{\circ })={\frac {10}{h}}$ $h={\frac {10}{\cot(30^{\circ })-\cot(50^{\circ })}}=11.20m$ $x=h\cot(50^{\circ })=9.40m$