三角学/拍频

我们之前看到，当两个波处于相位时，它们会互相加强；当它们处于反相位时，它们会互相抵消。当两个频率几乎相同但并不完全相同的波叠加时，它们可能一开始会互相加强，但随着时间的推移，频率的差异会导致它们开始互相抵消，然后又会互相加强。

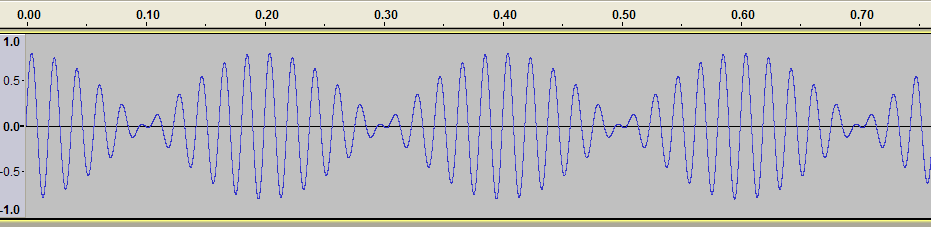
这正是上面图形中发生的情况。它展示了一个 50 Hz 音调和一个 55 Hz 音调的叠加。它是通过在免费音频软件“Audacity”中混合两个纯音调生成的。图像显示了大约 3/4 秒的音频。在一秒钟内，整体振幅达到最大值五次。听这种组合的声音，人们会听到一个介于 50 和 55 Hz 之间的单一音调，其响度似乎每秒变化五次，即 5 Hz。你不会听到两个独立的音调，一个在 50 Hz，另一个在 55 Hz。

这个 5 Hz 的音调称为拍频。

这里有一个按钮，可以播放通过组合两个较高频率的声音（220 Hz 音调和 222 Hz 音调）生成的拍频声音。

数学

从数学上来说，我们添加了两个频率非常接近的声音，但最终的结果似乎是两个频率非常不同的声音的乘积。这些频率是什么？一个是平均值，即 52.5 Hz。另一个乍一看似乎是差值，即 5 Hz，但实际上是差值的一半，因为一个 5 Hz 的正弦波在一秒钟内会达到最大值（忽略正负号）十次。

所以，一个频率是差值的一半，另一个频率是平均值。我们可以使用正弦的加法公式来理解从数学上来说，两个正弦的和如何变成一个积（正弦和余弦的积）。

我们添加的单个波形是

$\displaystyle \sin(\lambda _{1}t)$ $\displaystyle \sin(\lambda _{2}t)$

$\displaystyle \lambda _{1}=50\times 2\pi$ $\displaystyle \lambda _{2}=55\times 2\pi$

以及

为了得到 50 Hz 和 55 Hz 的频率，我们可以将

$\displaystyle \sigma =(\lambda _{1}+\lambda _{2})/2$

$\displaystyle h=(\lambda _{1}-\lambda _{2})/2$

然后用这两个新变量重新表达 $\displaystyle \lambda _{1}$ 和 $\displaystyle \lambda _{2}$。

$\displaystyle \lambda _{1}=\sigma +h$

$\displaystyle \lambda _{2}=\sigma -h$

现在我们有

$\displaystyle \sin(\lambda _{1}t)=\sin(\sigma t+ht)=\sin(\sigma t)\cos(ht)+\cos(\sigma t)\sin(ht)$

$\displaystyle \sin(\lambda _{2}t)=\sin(\sigma t-ht)=\sin(\sigma t)\cos(ht)-\cos(\sigma t)\sin(ht)$

在验证这两个公式是否遵循正弦加法公式之前，请勿继续阅读本页！不检查步骤就阅读本页并不能帮助你更好地使用数学。

因此，我们可以将这两个公式结合起来，得到

$\displaystyle \sin(\lambda _{1}t)+\sin(\lambda _{2}t)=2\sin(\sigma t)\cos(ht)$

也就是说

$\displaystyle \sin(\lambda _{1}t)+\sin(\lambda _{2}t)=2\sin \left({\frac {(\lambda _{1}+\lambda _{2})t}{2}}\right)\cos \left({\frac {(\lambda _{1}-\lambda _{2})t}{2}}\right)$

我们将两个正弦波的和表示为正弦和余弦的乘积。正如预期的那样，正弦波的频率是两个被组合波频率的平均值，而余弦波的频率是频率差的一半。