此页面从维基百科导入 。需要大量修改才能适合教科书。我们希望强调如何计算切比雪夫多项式,以及如何在 [0,1] 上使用它们进行函数逼近。
切比雪夫多项式 ,以 帕夫努提·切比雪夫 命名,[ 1]
我们通常区分
第一类切比雪夫多项式,记为T n cos {\displaystyle \cos }
第二类切比雪夫多项式,记为U n sin {\displaystyle \sin } 字母T 切比雪夫 的另一种转写方式是Tchebycheff (法语)或Tschebyschow (德语)。
切比雪夫多项式T n U n n 次多项式,并且任何一种切比雪夫多项式序列都构成一个“多项式序列”。
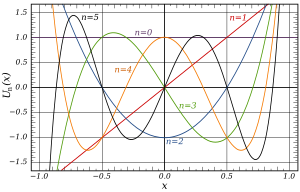
在域 −1 < x < 1 中,前几个第一类切比雪夫多项式:平坦T 0 T 1 T 2 T 3 T 4 T 5 前几个第一类切比雪夫多项式是
T 0 ( x ) = 1 {\displaystyle T_{0}(x)=1} T 1 ( x ) = x {\displaystyle T_{1}(x)=x} T 2 ( x ) = 2 x 2 − 1 {\displaystyle T_{2}(x)=2x^{2}-1} T 3 ( x ) = 4 x 3 − 3 x {\displaystyle T_{3}(x)=4x^{3}-3x} T 4 ( x ) = 8 x 4 − 8 x 2 + 1 {\displaystyle T_{4}(x)=8x^{4}-8x^{2}+1} T 5 ( x ) = 16 x 5 − 20 x 3 + 5 x {\displaystyle T_{5}(x)=16x^{5}-20x^{3}+5x} T 6 ( x ) = 32 x 6 − 48 x 4 + 18 x 2 − 1 {\displaystyle T_{6}(x)=32x^{6}-48x^{4}+18x^{2}-1} T 7 ( x ) = 64 x 7 − 112 x 5 + 56 x 3 − 7 x {\displaystyle T_{7}(x)=64x^{7}-112x^{5}+56x^{3}-7x} T 8 ( x ) = 128 x 8 − 256 x 6 + 160 x 4 − 32 x 2 + 1 {\displaystyle T_{8}(x)=128x^{8}-256x^{6}+160x^{4}-32x^{2}+1} T 9 ( x ) = 256 x 9 − 576 x 7 + 432 x 5 − 120 x 3 + 9 x {\displaystyle T_{9}(x)=256x^{9}-576x^{7}+432x^{5}-120x^{3}+9x} 在域 −1 < x < 1 中,第二类切比雪夫多项式的最初几个:图中的扁平U 0 U 1 U 2 U 3 U 4 U 5 U n n + 1U n n + 1)(−1)n 第二类切比雪夫多项式的最初几个是
U 0 ( x ) = 1 {\displaystyle U_{0}(x)=1} U 1 ( x ) = 2 x {\displaystyle U_{1}(x)=2x} U 2 ( x ) = 4 x 2 − 1 {\displaystyle U_{2}(x)=4x^{2}-1} U 3 ( x ) = 8 x 3 − 4 x {\displaystyle U_{3}(x)=8x^{3}-4x} U 4 ( x ) = 16 x 4 − 12 x 2 + 1 {\displaystyle U_{4}(x)=16x^{4}-12x^{2}+1} U 5 ( x ) = 32 x 5 − 32 x 3 + 6 x {\displaystyle U_{5}(x)=32x^{5}-32x^{3}+6x} U 6 ( x ) = 64 x 6 − 80 x 4 + 24 x 2 − 1 {\displaystyle U_{6}(x)=64x^{6}-80x^{4}+24x^{2}-1} U 7 ( x ) = 128 x 7 − 192 x 5 + 80 x 3 − 8 x {\displaystyle U_{7}(x)=128x^{7}-192x^{5}+80x^{3}-8x} U 8 ( x ) = 256 x 8 − 448 x 6 + 240 x 4 − 40 x 2 + 1 {\displaystyle U_{8}(x)=256x^{8}-448x^{6}+240x^{4}-40x^{2}+1} U 9 ( x ) = 512 x 9 − 1024 x 7 + 672 x 5 − 160 x 3 + 10 x {\displaystyle U_{9}(x)=512x^{9}-1024x^{7}+672x^{5}-160x^{3}+10x} 定义 T n ( x ) {\displaystyle T_{n}(x)} T n ( x ) {\displaystyle T_{n}(x)}
T n ( x ) = cos ( n arccos ( x ) ) , x ∈ [ − 1 , 1 ] {\displaystyle T_{n}(x)=\cos {\big (}n\arccos(x){\big )},\quad x\in [-1,1]} 换句话说, T n ( x ) {\displaystyle T_{n}(x)} cos ( θ ) {\displaystyle \cos(\theta )} cos ( n θ ) {\displaystyle \cos(n\theta )}
例如
T 3 ( x ) = 4 x 3 − 3 x {\displaystyle T_{3}(x)=4x^{3}-3x} 直接来自
cos ( 3 θ ) = 4 cos 3 ( θ ) − 3 cos ( θ ) {\displaystyle \cos(3\theta )=4\cos ^{3}(\theta )-3\cos(\theta )}
T 0 ( x ) = 1 T 1 ( x ) = x T n + 1 ( x ) = 2 x T n ( x ) − T n − 1 ( x ) {\displaystyle {\begin{aligned}T_{0}(x)&=1\\T_{1}(x)&=x\\T_{n+1}(x)&=2xT_{n}(x)-T_{n-1}(x)\end{aligned}}}
cos ( ( n + 1 ) θ ) = 2 cos ( θ ) cos ( n θ ) − cos ( ( n − 1 ) θ ) {\displaystyle \cos {\big (}(n+1)\theta {\big )}=2\cos(\theta )\cos(n\theta )-\cos {\big (}(n-1)\theta {\big )}} 这是从余弦加法公式推导的关系的重新排列
cos ( n θ + θ ) + cos ( n θ − θ ) = 2 cos ( n θ ) cos ( θ ) {\displaystyle \cos(n\theta +\theta )+\cos(n\theta -\theta )=2\cos(n\theta )\cos(\theta )} 的特殊情况,其中 ϕ = n θ {\displaystyle \phi =n\theta }
cos ( ϕ + θ ) + cos ( ϕ − θ ) = 2 cos ( ϕ ) cos ( θ ) {\displaystyle \cos(\phi +\theta )+\cos(\phi -\theta )=2\cos(\phi )\cos(\theta )} 我们在将两个波加在一起时看到的拍频。
如果在一个区间 ( 0 , 1 ) {\displaystyle \displaystyle (0,1)}
0.7123 + 1.543 x + 0.311 x 2 + 0.0172 x 3 {\displaystyle \displaystyle 0.7123+1.543x+0.311x^{2}+0.0172x^{3}} 为了近似它的值。因为 x {\displaystyle \displaystyle x} x n {\displaystyle \displaystyle x^{n}} x 4 {\displaystyle \displaystyle x^{4}}
在上面的例子多项式中,实际的数字只是虚构的数字,作为示例,没有特别的意义——如果你想知道为什么使用这些特定数字。
事实证明,从某种意义上说,截断级数不是用三次多项式近似原始函数的实际值的最佳方法。一种更复杂但更好的方法使用切比雪夫多项式。
a 0 + a 1 T 1 ( x ) + a 2 T 2 ( x ) + a 3 T 3 ( x ) + ⋯ {\displaystyle \displaystyle a_{0}+a_{1}T_{1}(x)+a_{2}T_{2}(x)+a_{3}T_{3}(x)+\cdots } 其中 a 0 , a 1 , a 2 , a 3 ⋯ {\displaystyle \displaystyle a_{0},a_{1},a_{2},a_{3}\cdots } 3 ,我们又得到一个没有 x 4 {\displaystyle \displaystyle x^{4}}
实际例子:展开 (2-x)-1
1 2 − x = 1 2 + x 4 + x 2 8 + x 3 16 + . . . {\displaystyle \displaystyle {\frac {1}{2-x}}={\frac {1}{2}}+{\frac {x}{4}}+{\frac {x^{2}}{8}}+{\frac {x^{3}}{16}}+...} 快速检查一下...这个公式看起来合理吗?
代入 x = 0 {\displaystyle \displaystyle x=0} 1 / 2 {\displaystyle \displaystyle 1/2}
代入 x = 1 {\displaystyle \displaystyle x=1}
1 2 + 1 4 + 1 8 + 1 16 + ⋯ = 1 {\displaystyle \displaystyle {\frac {1}{2}}+{\frac {1}{4}}+{\frac {1}{8}}+{\frac {1}{16}}+\cdots =1} 这个公式看起来合理。
如果我们只取四项,那么在 x = 1 {\displaystyle \displaystyle x=1} 1 16 {\displaystyle \displaystyle {\frac {1}{16}}}
现在用切比雪夫多项式来表示这个公式
1 1 − x = 1 2 + T 1 ( x ) 4 + T 2 ( x ) 16 + T 3 ( x ) 64 + . . . {\displaystyle \displaystyle {\frac {1}{1-x}}={\frac {1}{2}}+{\frac {T_{1}(x)}{4}}+{\frac {T_{2}(x)}{16}}+{\frac {T_{3}(x)}{64}}+...} 展开后得到
0.53125 + 0.203125 x + 0.125 x 2 + 0.0625 x 3 {\displaystyle \displaystyle 0.53125+0.203125x+0.125x^{2}+0.0625x^{3}} 待办事项:添加图表显示最大误差更小。不幸的是,当前计算结果没有显示这一点。
嗯……看起来我需要重新计算切比雪夫系数。
切比雪夫多项式在逼近理论中很重要,因为切比雪夫多项式 *T**n* 的根被用作多项式插值的节点。得到的插值多项式最小化了龙格现象的问题,并在最大范数下提供了一个接近连续函数最佳逼近多项式的逼近。
定义切比雪夫多项式的不同方法会导致不同的显式公式,例如
T n ( x ) = { cos ( n arccos ( x ) ) x ∈ [ − 1 , 1 ] cosh ( n a r c c o s h ( x ) ) x ≥ 1 ( − 1 ) n cosh ( n a r c c o s h ( − x ) ) x ≤ − 1 {\displaystyle T_{n}(x)={\begin{cases}\cos {\big (}n\arccos(x){\big )}&\ x\in [-1,1]\\\cosh {\big (}n\,{\rm {arccosh}}(x){\big )}&\ x\geq 1\\(-1)^{n}\cosh {\big (}n\,{\rm {arccosh}}(-x){\big )}&\ x\leq -1\\\end{cases}}}
T n ( x ) = ( x − x 2 − 1 ) n + ( x + x 2 − 1 ) n 2 = ∑ k = 0 ⌊ n 2 ⌋ ( n 2 k ) ( x 2 − 1 ) k x n − 2 k = x n ∑ k = 0 ⌊ n 2 ⌋ ( n 2 k ) ( 1 − x − 2 ) k = n 2 ∑ k = 0 ⌊ n 2 ⌋ ( − 1 ) k ( n − k − 1 ) ! k ! ( n − 2 k ) ! ( 2 x ) n − 2 k ( n > 0 ) = n ∑ k = 0 n ( − 2 ) k ( n + k − 1 ) ! ( n − k ) ! ( 2 k ) ! ( 1 − x ) k ( n > 0 ) = 2 F 1 ( − n , n , 1 2 , 1 − x 2 ) {\displaystyle {\begin{aligned}T_{n}(x)&={\frac {{\big (}x-{\sqrt {x^{2}-1}}{\big )}^{n}+{\big (}x+{\sqrt {x^{2}-1}}{\big )}^{n}}{2}}\\&=\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }{\binom {n}{2k}}(x^{2}-1)^{k}x^{n-2k}\\&=x^{n}\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }{\binom {n}{2k}}(1-x^{-2})^{k}\\&={\frac {n}{2}}\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }(-1)^{k}{\frac {(n-k-1)!}{k!(n-2k)!}}~(2x)^{n-2k}\quad (n>0)\\&=n\sum _{k=0}^{n}(-2)^{k}{\frac {(n+k-1)!}{(n-k)!(2k)!}}(1-x)^{k}\quad (n>0)\\&=\,_{2}F_{1}\left(-n,n,{\frac {1}{2}},{\frac {1-x}{2}}\right)\\\end{aligned}}}
U n ( x ) = ( x + x 2 − 1 ) n + 1 − ( x − x 2 − 1 ) n + 1 2 x 2 − 1 = ∑ k = 0 ⌊ n 2 ⌋ ( n + 1 2 k + 1 ) ( x 2 − 1 ) k x n − 2 k = x n ∑ k = 0 ⌊ n 2 ⌋ ( n + 1 2 k + 1 ) ( 1 − x − 2 ) k = ∑ k = 0 ⌊ n 2 ⌋ ( 2 k − ( n + 1 ) k ) ( 2 x ) n − 2 k ( n > 0 ) = ∑ k = 0 ⌊ n 2 ⌋ ( − 1 ) k ( n − k k ) ( 2 x ) n − 2 k ( n > 0 ) = ∑ k = 0 n ( − 2 ) k ( n + k + 1 ) ! ( n − k ) ! ( 2 k + 1 ) ! ( 1 − x ) k ( n > 0 ) = ( n + 1 ) 2 F 1 ( − n , n + 2 , 3 2 , 1 − x 2 ) {\displaystyle {\begin{aligned}U_{n}(x)&={\frac {{\big (}x+{\sqrt {x^{2}-1}}{\big )}^{n+1}-{\big (}x-{\sqrt {x^{2}-1}}{\big )}^{n+1}}{2{\sqrt {x^{2}-1}}}}\\&=\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }{\binom {n+1}{2k+1}}(x^{2}-1)^{k}x^{n-2k}\\&=x^{n}\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }{\binom {n+1}{2k+1}}(1-x^{-2})^{k}\\&=\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }{\binom {2k-(n+1)}{k}}~(2x)^{n-2k}\quad (n>0)\\&=\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }(-1)^{k}{\binom {n-k}{k}}~(2x)^{n-2k}\quad (n>0)\\&=\sum _{k=0}^{n}(-2)^{k}{\frac {(n+k+1)!}{(n-k)!(2k+1)!}}(1-x)^{k}\quad (n>0)\\&=(n+1)\,_{2}F_{1}\left(-n,n+2,{\frac {3}{2}},{\frac {1-x}{2}}\right)\end{aligned}}} 其中 2 F 1 {\displaystyle _{2}F_{1}} 超几何函数 .
切比雪夫多项式在逼近理论中很重要,因为切比雪夫多项式 *T**n* 的根被用作多项式插值的节点。得到的插值多项式最小化了龙格现象的问题,并在最大范数下提供了一个接近连续函数最佳逼近多项式的逼近。
在微分方程 研究中,它们是切比雪夫微分方程 的解。
( 1 − x 2 ) y ″ − x y ′ + n 2 y = 0 {\displaystyle (1-x^{2})\,y''-x\,y'+n^{2}\,y=0\,\!} 和
( 1 − x 2 ) y ″ − 3 x y ′ + n ( n + 2 ) y = 0 {\displaystyle (1-x^{2})\,y''-3x\,y'+n(n+2)\,y=0\,\!} 分别对应第一类和第二类多项式。这些方程是 Sturm–Liouville 微分方程 的特例。
第一类切比雪夫多项式 由递归关系定义
T 0 ( x ) = 1 T 1 ( x ) = x T n + 1 ( x ) = 2 x T n ( x ) − T n − 1 ( x ) . {\displaystyle {\begin{aligned}T_{0}(x)&=1\\T_{1}(x)&=x\\T_{n+1}(x)&=2xT_{n}(x)-T_{n-1}(x).\end{aligned}}} T n 生成函数 为
∑ n = 0 ∞ T n ( x ) t n = 1 − t x 1 − 2 t x + t 2 . {\displaystyle \sum _{n=0}^{\infty }T_{n}(x)t^{n}={\frac {1-tx}{1-2tx+t^{2}}}.\,\!} 指数生成函数为
∑ n = 0 ∞ T n ( x ) t n n ! = 1 2 ( e ( x − x 2 − 1 ) t + e ( x + x 2 − 1 ) t ) . {\displaystyle \sum _{n=0}^{\infty }T_{n}(x){\frac {t^{n}}{n!}}={1 \over 2}\left(e^{(x-{\sqrt {x^{2}-1}})t}+e^{(x+{\sqrt {x^{2}-1}})t}\right).\,\!} 第二类切比雪夫多项式 由 递归关系 定义
U 0 ( x ) = 1 U 1 ( x ) = 2 x U n + 1 ( x ) = 2 x U n ( x ) − U n − 1 ( x ) . {\displaystyle {\begin{aligned}U_{0}(x)&=1\\U_{1}(x)&=2x\\U_{n+1}(x)&=2xU_{n}(x)-U_{n-1}(x).\end{aligned}}} U n 生成函数
∑ n = 0 ∞ U n ( x ) t n = 1 1 − 2 t x + t 2 . {\displaystyle \sum _{n=0}^{\infty }U_{n}(x)t^{n}={\frac {1}{1-2tx+t^{2}}}.\,\!} 第一类切比雪夫多项式可以通过 三角恒等式 定义
T n ( x ) = cos ( n arccos x ) = cosh ( n a r c c o s h x ) {\displaystyle T_{n}(x)=\cos(n\arccos x)=\cosh(n\,\mathrm {arccosh} \,x)\,\!} 因此
T n ( cos ( ϑ ) ) = cos ( n ϑ ) {\displaystyle T_{n}(\cos(\vartheta ))=\cos(n\vartheta )\,\!} 对于 n = 0, 1, 2, 3, ..., 而第二类多项式满足
U n ( cos ( ϑ ) ) = sin ( ( n + 1 ) ϑ ) sin ϑ {\displaystyle U_{n}(\cos(\vartheta ))={\frac {\sin((n+1)\vartheta )}{\sin \vartheta }}\,\!} 这在结构上与狄利克雷核 D n ( x ) {\displaystyle D_{n}(x)\,\!}
D n ( x ) = sin ( ( 2 n + 1 ) ( x / 2 ) ) sin ( x / 2 ) = U 2 n ( cos ( x / 2 ) ) {\displaystyle D_{n}(x)={\frac {\sin((2n+1)(x/2))}{\sin(x/2)}}=U_{2n}(\cos(x/2))\,\!} cos(nx ) 是 cos(x ) 的 n 次多项式,这可以通过观察 cos(nx ) 是 棣莫弗公式 一侧的实部,而另一侧的实部是 cos(x ) 和 sin(x ) 的多项式,其中 sin(x ) 的所有幂都是偶数,因此可以通过恒等式 cos2 (x ) + sin2 (x ) = 1 替换。
这个恒等式与递归生成公式结合起来非常有用,因为它可以让人只用基本角的余弦来计算任何整数倍角的余弦。 评估前两个切比雪夫多项式
T 0 ( x ) = cos 0 x = 1 {\displaystyle T_{0}(x)=\cos \ 0x\ =1\,\!} 和
T 1 ( cos ( x ) ) = cos ( x ) {\displaystyle T_{1}(\cos(x))=\cos(x)\,\!} 可以很容易地确定
cos ( 2 ϑ ) = 2 cos ϑ cos ϑ − cos ( 0 ϑ ) = 2 cos 2 ϑ − 1 {\displaystyle \cos(2\vartheta )=2\cos \vartheta \cos \vartheta -\cos(0\vartheta )=2\cos ^{2}\,\vartheta -1\,\!} cos ( 3 ϑ ) = 2 cos ϑ cos ( 2 ϑ ) − cos ϑ = 4 cos 3 ϑ − 3 cos ϑ {\displaystyle \cos(3\vartheta )=2\cos \vartheta \cos(2\vartheta )-\cos \vartheta =4\cos ^{3}\,\vartheta -3\cos \vartheta \,\!} 等等。为了简单地检查结果是否合理,将等号两边的系数相加(即设置 ϑ {\displaystyle \vartheta } 2 − 1 ,后一个表达式中 1 = 4 − 3 。
两个直接推论是合成恒等式(或“嵌套属性”)
T n ( T m ( x ) ) = T n ⋅ m ( x ) . {\displaystyle T_{n}(T_{m}(x))=T_{n\cdot m}(x).\,\!} 以及复指数形式的切比雪夫多项式表达式:给定 z = a + bi ,
z n = | z | n ( cos ( n arccos a | z | ) + i sin ( n arccos a | z | ) ) = | z | n T n ( a | z | ) + i b | z | n − 1 U n − 1 ( a | z | ) . {\displaystyle {\begin{aligned}z^{n}&=|z|^{n}\left(\cos \left(n\arccos {\frac {a}{|z|}}\right)+i\sin \left(n\arccos {\frac {a}{|z|}}\right)\right)\\&=|z|^{n}T_{n}\left({\frac {a}{|z|}}\right)+ib\ |z|^{n-1}\ U_{n-1}\left({\frac {a}{|z|}}\right).\end{aligned}}} 切比雪夫多项式也可以定义为佩尔方程 的解
T n ( x ) 2 − ( x 2 − 1 ) U n − 1 ( x ) 2 = 1 {\displaystyle T_{n}(x)^{2}-(x^{2}-1)U_{n-1}(x)^{2}=1\,\!} 在环 R[x ] 中。[ 2]
T n ( x ) + U n − 1 ( x ) x 2 − 1 = ( x + x 2 − 1 ) n . {\displaystyle T_{n}(x)+U_{n-1}(x){\sqrt {x^{2}-1}}=(x+{\sqrt {x^{2}-1}})^{n}.\,\!} 第一类和第二类切比雪夫多项式之间有着密切的关系,它们可以通过以下方程来表示
d d x T n ( x ) = n U n − 1 ( x ) , n = 1 , … {\displaystyle {\frac {d}{dx}}\,T_{n}(x)=nU_{n-1}(x){\mbox{ , }}n=1,\ldots } T n ( x ) = 1 2 ( U n ( x ) − U n − 2 ( x ) ) . {\displaystyle T_{n}(x)={\frac {1}{2}}(U_{n}(x)-\,U_{n-2}(x)).} T n + 1 ( x ) = x T n ( x ) − ( 1 − x 2 ) U n − 1 ( x ) {\displaystyle T_{n+1}(x)=xT_{n}(x)-(1-x^{2})U_{n-1}(x)\,} T n ( x ) = U n ( x ) − x U n − 1 ( x ) . {\displaystyle T_{n}(x)=U_{n}(x)-x\,U_{n-1}(x).} 切比雪夫多项式导数的递归关系可以从这些关系中推导出
2 T n ( x ) = 1 n + 1 d d x T n + 1 ( x ) − 1 n − 1 d d x T n − 1 ( x ) , n = 1 , … {\displaystyle 2T_{n}(x)={\frac {1}{n+1}}\;{\frac {d}{dx}}T_{n+1}(x)-{\frac {1}{n-1}}\;{\frac {d}{dx}}T_{n-1}(x){\mbox{ , }}\quad n=1,\ldots } 此关系式在求解微分方程的切比雪夫谱方法 中使用。
等效地,这两个序列也可以从一对互递归 方程定义:
T 0 ( x ) = 1 {\displaystyle T_{0}(x)=1\,\!} U − 1 ( x ) = 0 {\displaystyle U_{-1}(x)=0\,\!} T n + 1 ( x ) = x T n ( x ) − ( 1 − x 2 ) U n − 1 ( x ) {\displaystyle T_{n+1}(x)=xT_{n}(x)-(1-x^{2})U_{n-1}(x)\,} U n ( x ) = x U n − 1 ( x ) + T n ( x ) {\displaystyle U_{n}(x)=xU_{n-1}(x)+T_{n}(x)\,} 这些可以从三角公式推导出;例如,如果 x = cos ϑ {\displaystyle x=\cos \vartheta }
T n + 1 ( x ) = T n + 1 ( cos ( ϑ ) ) = cos ( ( n + 1 ) ϑ ) = cos ( n ϑ ) cos ( ϑ ) − sin ( n ϑ ) sin ( ϑ ) = T n ( cos ( ϑ ) ) cos ( ϑ ) − U n − 1 ( cos ( ϑ ) ) sin 2 ( ϑ ) = x T n ( x ) − ( 1 − x 2 ) U n − 1 ( x ) . {\displaystyle {\begin{aligned}T_{n+1}(x)&=T_{n+1}(\cos(\vartheta ))\\&=\cos((n+1)\vartheta )\\&=\cos(n\vartheta )\cos(\vartheta )-\sin(n\vartheta )\sin(\vartheta )\\&=T_{n}(\cos(\vartheta ))\cos(\vartheta )-U_{n-1}(\cos(\vartheta ))\sin ^{2}(\vartheta )\\&=xT_{n}(x)-(1-x^{2})U_{n-1}(x).\\\end{aligned}}} 请注意,如果我们像某些著作一样,遵循将我们的U n U n +1
任何一种 n 次切比雪夫多项式在区间 [−1,1] 内有 n 个不同的简单根,称为切比雪夫根 。这些根有时被称为切比雪夫节点 ,因为它们用作多项式插值的节点 。使用三角定义和以下事实
cos ( π 2 ( 2 k + 1 ) ) = 0 {\displaystyle \cos \left({\frac {\pi }{2}}\,(2k+1)\right)=0} 可以很容易地证明T n
x k = cos ( π 2 2 k − 1 n ) , k = 1 , … , n . {\displaystyle x_{k}=\cos \left({\frac {\pi }{2}}\,{\frac {2k-1}{n}}\right),\quad k=1,\ldots ,n.} 类似地,U n
x k = cos ( k n + 1 π ) , k = 1 , … , n . {\displaystyle x_{k}=\cos \left({\frac {k}{n+1}}\pi \right),\quad k=1,\ldots ,n.} 第一类切比雪夫多项式的一个独特的性质是在区间 −1 ≤ x ≤ 1 上,所有 极值 的值都为 −1 或 1。因此,这些多项式只有两个有限的 临界值 ,这是 Shabat 多项式 的定义属性。第一类和第二类切比雪夫多项式都在端点处有极值,分别为
T n ( 1 ) = 1 {\displaystyle T_{n}(1)=1\,} T n ( − 1 ) = ( − 1 ) n {\displaystyle T_{n}(-1)=(-1)^{n}\,} U n ( 1 ) = n + 1 {\displaystyle U_{n}(1)=n+1\,} U n ( − 1 ) = ( n + 1 ) ( − 1 ) n . {\displaystyle U_{n}(-1)=(n+1)(-1)^{n}.\,} 多项式的导数可能不像直观那样简单。通过对多项式在三角形式上的微分,很容易证明
d T n d x = n U n − 1 {\displaystyle {\frac {dT_{n}}{dx}}=nU_{n-1}\,} d U n d x = ( n + 1 ) T n + 1 − x U n x 2 − 1 {\displaystyle {\frac {dU_{n}}{dx}}={\frac {(n+1)T_{n+1}-xU_{n}}{x^{2}-1}}\,} d 2 T n d x 2 = n n T n − x U n − 1 x 2 − 1 = n ( n + 1 ) T n − U n x 2 − 1 . {\displaystyle {\frac {d^{2}T_{n}}{dx^{2}}}=n{\frac {nT_{n}-xU_{n-1}}{x^{2}-1}}=n{\frac {(n+1)T_{n}-U_{n}}{x^{2}-1}}.\,} 由于在 x = 1x = −1不确定形式 ,具体来说),最后两个公式在数值上可能会有问题。可以证明
d 2 T n d x 2 | x = 1 = n 4 − n 2 3 , {\displaystyle {\frac {d^{2}T_{n}}{dx^{2}}}{\Bigg |}_{x=1}\!\!={\frac {n^{4}-n^{2}}{3}},} d 2 T n d x 2 | x = − 1 = ( − 1 ) n n 4 − n 2 3 . {\displaystyle {\frac {d^{2}T_{n}}{dx^{2}}}{\Bigg |}_{x=-1}\!\!=(-1)^{n}{\frac {n^{4}-n^{2}}{3}}.} 实际上,以下更一般的公式成立:
d p T n d x p | x = ± 1 = ( ± 1 ) n + p ∏ k = 0 p − 1 n 2 − k 2 2 k + 1 . {\displaystyle {\frac {d^{p}T_{n}}{dx^{p}}}{\Bigg |}_{x=\pm 1}\!\!=(\pm 1)^{n+p}\prod _{k=0}^{p-1}{\frac {n^{2}-k^{2}}{2k+1}}.} 该结果在特征值问题的数值解法中非常有用。
关于积分,T n
∫ U n d x = T n + 1 n + 1 {\displaystyle \int U_{n}\,dx={\frac {T_{n+1}}{n+1}}\,} 第一类多项式的递推关系涉及导数,因此可以建立
∫ T n d x = 1 2 ( T n + 1 n + 1 − T n − 1 n − 1 ) = n T n + 1 n 2 − 1 − x T n n − 1 . {\displaystyle \int T_{n}\,dx={\frac {1}{2}}\left({\frac {T_{n+1}}{n+1}}-{\frac {T_{n-1}}{n-1}}\right)={\frac {nT_{n+1}}{n^{2}-1}}-{\frac {xT_{n}}{n-1}}.\,} T N ( x ) {\displaystyle T_{N}(x)} U N ( x ) {\displaystyle U_{N}(x)} 正交多项式 。第一类多项式关于权重
1 1 − x 2 {\displaystyle {\frac {1}{\sqrt {1-x^{2}}}}} 在区间 ( − 1 , 1 ) {\displaystyle (-1,1)}
∫ − 1 1 T n ( x ) T m ( x ) d x 1 − x 2 = { 0 : n ≠ m π : n = m = 0 π 2 : n = m ≠ 0 {\displaystyle \int \limits _{-1}^{1}T_{n}(x)T_{m}(x)\,{\frac {dx}{\sqrt {1-x^{2}}}}={\begin{cases}0&:n\neq m\\\pi &:n=m=0\\{\frac {\pi }{2}}&:n=m\neq 0\end{cases}}} 这可以通过令 x = cos ( ϑ ) {\displaystyle x=\cos(\vartheta )} T n ( cos ( ϑ ) ) = cos ( n ϑ ) {\displaystyle T_{n}(\cos(\vartheta ))=\cos(n\vartheta )}
类似地,第二类多项式关于权重
1 − x 2 {\displaystyle {\sqrt {1-x^{2}}}} 在区间 [ − 1 , 1 ] {\displaystyle [-1,1]}
∫ − 1 1 U n ( x ) U m ( x ) 1 − x 2 d x = { 0 : n ≠ m π 2 : n = m {\displaystyle \int \limits _{-1}^{1}U_{n}(x)U_{m}(x){\sqrt {1-x^{2}}}\,dx={\begin{cases}0&:n\neq m\\{\frac {\pi }{2}}&:n=m\end{cases}}} (注意,权重 1 − x 2 {\displaystyle {\sqrt {1-x^{2}}}} 维格纳半圆分布 的密度)。
T n {\displaystyle T_{n}}
∑ k = 0 N − 1 T i ( x k ) T j ( x k ) = { 0 : i ≠ j N : i = j = 0 N 2 : i = j ≠ 0 {\displaystyle \sum _{k=0}^{N-1}{T_{i}(x_{k})T_{j}(x_{k})}={\begin{cases}0&:i\neq j\\N&:i=j=0\\{\frac {N}{2}}&:i=j\neq 0\end{cases}}} 其中 x k {\displaystyle x_{k}} N {\displaystyle N} 高斯 –勒让德 零点 T N ( x ) {\displaystyle T_{N}(x)}
x k = cos ( π ( k + 1 2 ) N ) {\displaystyle x_{k}=\cos \left({\frac {\pi \left(k+{\frac {1}{2}}\right)}{N}}\right)} 对于任何给定的 n ≥ 1,在所有首项系数为 1 的 n 次多项式中,
f ( x ) = 1 2 n − 1 T n ( x ) {\displaystyle f(x)={\frac {1}{2^{n-1}}}T_{n}(x)} 是那个在区间 [−1, 1] 上的最大绝对值最小的多项式。
这个最大绝对值为
1 2 n − 1 {\displaystyle {\frac {1}{2^{n-1}}}} 并且|ƒ(x )| 恰好在 n + 1
x = cos k π n for 0 ≤ k ≤ n . {\displaystyle x=\cos {\frac {k\pi }{n}}{\text{ for }}0\leq k\leq n.} 假设 w n ( x ) {\displaystyle w_{n}(x)} n 次多项式,它在区间 [−1, 1] 上的最大绝对值小于 1 2 n − 1 {\displaystyle {\frac {1}{2^{n-1}}}}
我们定义
f n ( x ) = 1 2 n − 1 T n ( x ) − w n ( x ) {\displaystyle f_{n}(x)={\frac {1}{2^{n-1}}}T_{n}(x)-w_{n}(x)} 因为在 T n {\displaystyle T_{n}} | w n ( x ) | < | 1 2 n − 1 T n ( x ) | {\displaystyle |w_{n}(x)|<|{\frac {1}{2^{n-1}}}T_{n}(x)|}
f n ( x ) > 0 for x = cos 2 k π n where 0 ≤ 2 k ≤ n {\displaystyle f_{n}(x)>0{\text{ for }}x=\cos {\frac {2k\pi }{n}}{\text{ where }}0\leq 2k\leq n} f n ( x ) < 0 for x = cos ( 2 k + 1 ) π n where 0 ≤ 2 k + 1 ≤ n {\displaystyle f_{n}(x)<0{\text{ for }}x=\cos {\frac {(2k+1)\pi }{n}}{\text{ where }}0\leq 2k+1\leq n} f n ( x ) {\displaystyle f_{n}(x)} n - 1介值定理 ,它至少有 n 个根,但这对于一个 n - 1
切比雪夫多项式是超球面多项式或 盖根鲍尔多项式 的特例,而盖根鲍尔多项式本身是 雅可比多项式 的特例。
T n ( x ) = 1 ( n − 1 2 n ) P n − 1 2 , − 1 2 ( x ) = n 2 C n 0 ( x ) , {\displaystyle T_{n}(x)={\frac {1}{n-{\frac {1}{2}} \choose n}}P_{n}^{-{\frac {1}{2}},-{\frac {1}{2}}}(x)={\frac {n}{2}}C_{n}^{0}(x),} U n ( x ) = 1 2 ( n + 1 2 n ) P n 1 2 , 1 2 ( x ) = C n 1 ( x ) . {\displaystyle U_{n}(x)={\frac {1}{2{n+{\frac {1}{2}} \choose n}}}P_{n}^{{\frac {1}{2}},{\frac {1}{2}}}(x)=C_{n}^{1}(x).} 对于每一个非负整数 n ,T n x ) 和 U n x ) 都是 n 次多项式。它们是 x 的 偶函数或奇函数 ,因为 n 是偶数或奇数,所以当它们被写成 x 的多项式时,它们分别只有偶数次项或奇数次项。事实上,
T n ( 1 − 2 x 2 ) = ( − 1 ) n T 2 n ( x ) {\displaystyle T_{n}\left(1-2x^{2}\right)=(-1)^{n}T_{2n}(x)} 和
U n ( 1 − 2 x 2 ) x = ( − 1 ) n U 2 n + 1 ( x ) . {\displaystyle U_{n}\left(1-2x^{2}\right)x=(-1)^{n}U_{2n+1}(x).} T n 2n − 1 ,如果 1 ≤ n ,但如果 0 = n ,则为 1。
T n 李萨如曲线 的特例,频率比为 n 。
一些多项式序列,如 卢卡斯多项式 (L n 迪克森多项式 (D n 斐波那契多项式 (F n T n U n
第一类切比雪夫多项式满足以下关系
T j ( x ) T k ( x ) = 1 2 ( T j + k ( x ) + T | j − k | ( x ) ) , ∀ j , k ≥ 0 , {\displaystyle T_{j}(x)T_{k}(x)={\frac {1}{2}}\left(T_{j+k}(x)+T_{|j-k|}(x)\right),\quad \forall j,k\geq 0,\,} 这很容易从余弦的积化和公式 推导出来。第二类多项式满足类似的关系
T j ( x ) U k ( x ) = 1 2 ( U j + k ( x ) + U k − j ( x ) ) , ∀ j , k {\displaystyle T_{j}(x)U_{k}(x)={\frac {1}{2}}\left(U_{j+k}(x)+U_{k-j}(x)\right),\quad \forall j,k} 类似于公式
T n ( cos θ ) = cos ( n θ ) {\displaystyle T_{n}(\cos \theta )=\cos(n\theta )} 我们有类似的公式
T 2 n + 1 ( sin θ ) = ( − 1 ) n sin ( ( 2 n + 1 ) θ ) {\displaystyle T_{2n+1}(\sin \theta )=(-1)^{n}\sin((2n+1)\theta )}
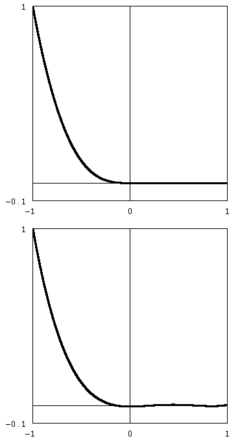
非光滑函数(顶部)y = −x 3 H (−x )H 是Heaviside 阶跃函数 ,以及(底部)其 Chebyshev 展开的第 5 个偏和。第 7 个和在图形分辨率下与原始函数无法区分。 在适当的Sobolev 空间 中,Chebyshev 多项式集形成一个完整的 基集 ,因此相同空间中的函数可以在 −1 ≤ x ≤ 1 上通过以下展开式表示:[ 3]
f ( x ) = ∑ n = 0 ∞ a n T n ( x ) . {\displaystyle f(x)=\sum _{n=0}^{\infty }a_{n}T_{n}(x).} 此外,如前所述,Chebyshev 多项式形成了一个正交的 基,这意味着(除其他外)系数 a n 内积 轻松确定。这个和被称为Chebyshev 级数 或Chebyshev 展开 。
由于 Chebyshev 级数与傅里叶余弦级数 通过变量变化相关联,因此所有适用于傅里叶级数 的定理、恒等式等都有一个 Chebyshev 对应物。[ 3]
Chebyshev 多项式构成一个完整的 正交系统。
如果函数是分段 光滑 且连续 ,则 Chebyshev 级数收敛于 ƒ(x )。在大多数情况下,光滑度要求可以放宽 - 只要 ƒ(x ) 及其导数的间断点有限。
在间断点处,级数将收敛于左右极限的平均值。 从傅里叶级数 继承的大量定理和恒等式使 Chebyshev 多项式成为数值分析 中的重要工具;例如,它们是谱方法 中最流行的通用基函数[ 3] 吉布斯现象 仍然是一个问题)。
考虑 log ( 1 + x ) {\displaystyle \log(1+x)}
log ( 1 + x ) = ∑ n = 0 ∞ a n T n ( x ) {\displaystyle \log(1+x)=\sum _{n=0}^{\infty }a_{n}T_{n}(x)} 可以通过应用内积 或离散正交性条件来找到系数 a n {\displaystyle a_{n}}
∫ − 1 1 T m ( x ) log ( 1 + x ) 1 − x 2 d x = ∑ n = 0 ∞ a n ∫ − 1 1 T m ( x ) T n ( x ) 1 − x 2 d x {\displaystyle \int \limits _{-1}^{1}{\frac {T_{m}(x)\log(1+x)}{\sqrt {1-x^{2}}}}dx=\sum _{n=0}^{\infty }a_{n}\int \limits _{-1}^{1}{\frac {T_{m}(x)T_{n}(x)}{\sqrt {1-x^{2}}}}dx} 得到
a n = { − log ( 2 ) : n = 0 − 2 ( − 1 ) n n : n > 0 {\displaystyle a_{n}={\begin{cases}-\log(2)&:n=0\\{\dfrac {-2(-1)^{n}}{n}}&:n>0\end{cases}}} 或者,当您无法评估您尝试逼近的函数的内积时,离散正交性条件给出
a n = 2 − δ 0 n N ∑ k = 0 N − 1 T n ( x k ) log ( 1 + x k ) {\displaystyle a_{n}={\frac {2-\delta _{0n}}{N}}\sum _{k=0}^{N-1}T_{n}(x_{k})\log(1+x_{k})} 其中 δ i j {\displaystyle \delta _{ij}} 克罗内克德尔塔 函数,而 x k {\displaystyle x_{k}} N {\displaystyle N} T N ( x ) {\displaystyle T_{N}(x)} 高斯-勒让德 零点。
x k = cos ( π ( k + 1 2 ) N ) {\displaystyle x_{k}=\cos \left({\frac {\pi \left(k+{\frac {1}{2}}\right)}{N}}\right)} 这使得我们可以通过离散余弦变换 非常有效地计算系数 a n {\displaystyle a_{n}}
a n = 2 − δ 0 n N ∑ k = 0 N − 1 cos ( n π ( k + 1 2 ) N ) log ( 1 + x k ) {\displaystyle a_{n}={\frac {2-\delta _{0n}}{N}}\sum _{k=0}^{N-1}\cos \left({\frac {n\pi \left(k+{\frac {1}{2}}\right)}{N}}\right)\log(1+x_{k})} 为了提供另一个示例
( 1 − x 2 ) α = − 1 π Γ ( 1 2 + α ) Γ ( α + 1 ) + 2 1 − 2 α ∑ n = 0 ( − 1 ) n ( 2 α α − n ) T 2 n ( x ) = 2 − 2 α ∑ n = 0 ( − 1 ) n ( 2 α + 1 α − n ) U 2 n ( x ) . {\displaystyle {\begin{aligned}(1-x^{2})^{\alpha }=&-{\frac {1}{\sqrt {\pi }}}{\frac {\Gamma ({\frac {1}{2}}+\alpha )}{\Gamma (\alpha +1)}}+2^{1-2\alpha }\sum _{n=0}(-1)^{n}{2\alpha \choose \alpha -n}T_{2n}(x)\\=&2^{-2\alpha }\sum _{n=0}(-1)^{n}{2\alpha +1 \choose \alpha -n}U_{2n}(x).\end{aligned}}}
的部分和
f ( x ) = ∑ n = 0 ∞ a n T n ( x ) {\displaystyle f(x)=\sum _{n=0}^{\infty }a_{n}T_{n}(x)} 在各种函数的近似和微分方程的求解中非常有用(参见谱方法)。确定系数 *a**n* 的两种常用方法是通过使用内积,如在伽辽金方法中,以及通过使用与插值相关的配置方法。
作为插值函数,(*N* − 1)th 部分和的 *N* 个系数通常是在切比雪夫-高斯-勒让德点(或勒让德网格)上获得的,这会导致最小误差并避免与均匀网格相关的龙格现象。
x i = − cos ( i π N − 1 ) ; i = 0 , 1 , … , N − 1. {\displaystyle x_{i}=-\cos \left({\frac {i\pi }{N-1}}\right);\qquad \ i=0,1,\dots ,N-1.} 任意 *N* 次多项式可以用第一类切比雪夫多项式表示。这样的多项式 *p*(*x*) 具有以下形式
p ( x ) = ∑ n = 0 N a n T n ( x ) . {\displaystyle p(x)=\sum _{n=0}^{N}a_{n}T_{n}(x).} 可以用克伦肖算法对切比雪夫形式的多项式进行求值。
扩展多项式在某种意义上等效于第一类切比雪夫多项式,但它们使人们能够在某些情况下避免平方根和常规三角函数,尤其是在有理三角学中。
↑ 切比雪夫多项式首次出现在:P. L. Chebyshev (1854) "Théorie des mécanismes connus sous le nom de parallélogrammes," Mémoires des Savants étrangers présentés à l’Académie de Saint-Pétersbourg , vol. 7, pages 539-586. ↑ Jeroen Demeyer Diophantine Sets over Polynomial Rings and Hilbert's Tenth Problem for Function Fields , Ph.D. theses (2007), p.70. ↑ a b c Boyd, John P. (2001). 切比雪夫与傅立叶谱方法 (PDF) (第二版). 多佛. ISBN 0486411834 ↑ 切比雪夫插值:互动之旅

























![{\displaystyle T_{n}(x)=\cos {\big (}n\arccos(x){\big )},\quad x\in [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbec6621a9d9b9ec4aec14c7fa34603dd72ef5c5)























![{\displaystyle T_{n}(x)={\begin{cases}\cos {\big (}n\arccos(x){\big )}&\ x\in [-1,1]\\\cosh {\big (}n\,{\rm {arccosh}}(x){\big )}&\ x\geq 1\\(-1)^{n}\cosh {\big (}n\,{\rm {arccosh}}(-x){\big )}&\ x\leq -1\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17c3424f54958b0288161b2f5159c2cb15a06f25)


































































![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)



































