三角学/爱好者/严格的三角学
此页面最初作为三角学最基本概念的介绍,例如测量角度。做得恰当,这将是一个高级主题。此页面现在已移动/重命名为第 3 册,以承担该角色,并且需要进行大量修订。某些仍然在此处的内容可能需要重新集成到第 1 册中 |

当两条直线相交时形成一个角;交点称为顶点。我们可以将角视为两条直线相遇时之间的楔形空间。请注意,如果两条直线都通过交点延伸,实际上有四个角。
角的大小是两条直线之间旋转的度数。我们必须旋转一条直线以与另一条直线相遇的次数越多,角度就越大。
假设您想精确地测量两条直线之间的角度,以便可以告诉远处的朋友:在两条直线相遇处画一个圆,确保圆足够小以穿过两条直线,但足够大以让您测量圆边缘的距离,即圆周,在两个交叉点之间。显然,此距离取决于圆的大小,但只要您告诉您的朋友所用圆的半径和圆周上的长度,您的朋友就可以精确地重建角度。
角度是由绕其端点旋转射线确定的。射线的起始位置称为角的始边。射线的结束位置称为终边。射线的端点称为其顶点。正角是由逆时针旋转产生的。负角是由顺时针旋转产生的。
因此,角度有四个部分:它的顶点、它的始边、它的终边和它的旋转。
当角度以使它的顶点位于原点,而它的始边为正 x 轴的方式在笛卡尔坐标系中绘制时,据说它处于标准位置。

三角形是一种具有三条直边的平面(扁平)形状。在三角形的每两条边之间形成一个角,三角形有三个角,因此得名三-角。因此,三角形有三个直边和三个角。
如果你给我三个长度,我只能用它们组成一个三角形,前提是最大长度小于另外两个长度的总和。不能构成三角形三条边的三个长度是你的身高,最近树的高度,从树顶到太阳中心的距离。
角度不受直线长度的影响:角度在缩放变换下是不变的,也就是说
如果你使三角形变大,
但保持边之间的比率相同,
它的角度不会改变。
一个特别重要的角度是直角:正方形或长方形每个角的角度。长方形总是可以通过从长方形的一个角到对角线画一条线来分成两个三角形。
每个直角三角形都是长方形的一半也是正确的。

长方形有四条边;它们通常有两种不同的长度:两条长边和两条短边。(所有边都相等的长方形是正方形。)当我们将长方形分成两个直角三角形时,每个三角形都具有长方形的长边和短边,以及分裂线的副本。
因此,直角三角形的面积是将它分割的长方形面积的一半。看一个直角三角形,我们可以知道该长方形的长边和短边是什么;它们是直角相交的边,即直线。完整长方形的面积是长边乘以短边。因此,直角三角形的面积是一半。

可以使用以下步骤仅使用圆(可以使用圆规绘制)和直线来平分任何角
- 将角的顶点称为 O。以 O 为中心画一个圆。
- 标记圆与每条射线的交点。将这些点称为 A 和 B。
- 以 A 和 B 为中心画圆,半径相等,但确保这些半径足够大以使圆在两点处相交。一种肯定的方法是绘制线段 AB 并使圆的半径等于该线段的长度。在图中,圆 A 和 B 显示为圆的近一半部分。
- 标记这些圆的交点,并将这两个点用一条直线连接起来。这条直线平分了原始角。
在《几何原本》的第 1 卷命题 9中可以找到这条线平分角的证明。
给定一个直角,我们可以使用此过程无限地分割该直角以形成任何二进制分数(即 ,例如 )。因此,我们可以用直角来测量任何角度。也就是说,在一个测量系统中,直角的大小被认为是 1。
为了说明弧度的三条边是如何相互关联的,请尝试以下思维实验。
- 假设你有一根绳子,它的长度正好等于圆的半径。
- 假设你在同一个圆中画了一个弧度。弧度有三个点。一个是圆心,另外两个是在圆周上,弧度的边与圆相交的地方。
- 将绳子的一端固定在弧度与圆周相交的点之一上。
- 拿起绳子的另一端,从你在上面步骤 2 中选择的点开始,沿着圆周向弧度与圆周相交的第二个点移动,直到绳子拉紧。
- 你会看到绳子的末端会经过第二个点。
- 这是因为绳子现在是一条直线。然而,弧度的第三边是弧线,而不是直线。即使弧度有三条相等的边,弧线的弯曲也导致弧度与圆周相交的两个点比它们到三角形第三个点的距离更近,在这个例子中,三角形的第三个点是圆心。
- 现在,在绳子仍然拉紧的情况下,找到绳子的中点,然后将其拉到圆周上,同时允许绳子的末端沿着圆周移动。绳子的末端现在更靠近第二个点,因为绳子的路径更接近圆周的路径。
- 我们可以通过将绳子的每个新部分分成两半并将其拉向圆周,来不断改善绳子路径与圆周路径的吻合度。
使用不同大小的圆来测量弧度是否会产生不同的角度?也许使用大圆的半径会产生与使用小圆的半径产生的角度不同的角度。答案是否定的。

回想我们在上面小节中的弧度和圆。在第一个圆内画一个半径为第一个圆半径一半的第二个圆,并与第一个圆共用圆心。你会看到你在较小的圆内创建了一个新的弧度,该弧度与较大圆内的弧度具有相同的角度。我们知道从圆心出发的弧度的两条边等于它们各自圆的半径。我们也知道较大圆的弧度的第三边(弧线)也等于较大圆的半径。但是我们怎么知道较小圆的弧度的第三边(沿着较小圆圆周的弧线)等于较小圆的半径呢?为了说明我们为什么知道较小圆的弧度的第三边等于它的半径,我们首先将每个弧度与圆相交的两个点彼此连接起来。通过这样做,你将创建两个等腰三角形(有两条相等的边和两个相等的角)。
等腰三角形有两个相等的角和两条相等的边。如果你知道任何等腰三角形的一个角和组成该角的两条边的长度,那么你就可以很容易地推导出等腰三角形的剩余特征。例如,如果等腰三角形的两条等边相交形成一个等于 40o 的角,那么你知道剩下的两个角都必须等于 70º。由于我们知道我们两个等腰三角形的等边构成了我们已知的角度,那么我们可以推断出我们两个弧度(当转换成带有直线的等腰三角形时)具有相同的第二和第三个角。我们还知道具有相同角度的三角形,无论它们的大小如何,它们的边长都将保持一个恒定的比例。例如,我们可以推断出一个等腰三角形的边长将分别为 2 米、4 米和 4 米,如果我们知道一个具有相同角度的等腰三角形的边长分别为 1 米、2 米和 2 米。因此,在我们的例子中,由第二个较小的圆形成的等腰三角形的第三边将正好等于由较大圆形成的等腰三角形的第三边的一半。共享相同角度的两个三角形的边长之间的关系,也存在于共享相同中心的两个圆的半径和周长之间的关系中——它们将共享完全相同的比例。那么,在我们的例子中,由于我们的第二个较小的圆的半径正好是较大圆的一半,因此较小圆的弧度与圆周相交的两个点之间的周长(我们已经证明它是较大圆上两个类似点之间的距离的一半)将共享完全相同的比例。就这样——圆的大小并不重要。
一旦我们有了 1 个弧度的角度,我们就可以将其分割成二进制分数,就像我们对直角所做的那样,得到一系列已知角度,用来测量未知角度。量角器是一种利用这种技术近似测量角度的工具。要使用量角器测量角度:将量角器上标记的中心点放在要测量的角度的角上,将量角器上的右手零弧度线与角度的一条线对齐,然后读出角度的另一条线与量角器边缘的交点。量角器通常是透明的,上面画有角度线,可以帮助你测量由短线形成的角度:这是允许的,因为角度不依赖于形成它们的线的长度。
如果我们同意用弧度测量角度,那么知道一些容易定义的角度的大小将很有用。当然,我们可以简单地画出角度,然后使用量角器非常精确地测量它们,尽管仍然只是近似值:但是,那样我们就是在做物理,而不是数学。
圆的周长与半径的长度之比定义为 2π,其中π是根据上面论证,不依赖于圆的大小的一个不变量。因此,如果我们从圆周上的一个给定点沿着圆周移动 2π 个半径,我们就会回到起点。我们必须得出结论,绕圆周运行一周形成的角度的大小为 2π 弧度。同样,绕圆周运行半周将是 π 弧度。想象一下,将一个圆沿着对称轴对折:形成的折痕将是一条直径,一条穿过圆心的直线。因此,直线具有 π 弧度的角度。
再次将半圆对折,会得到一个四分之一圆,因此它的角度大小必须是 π/2 弧度。四分之一圆是一个直角吗?为了说明它是直角:画一个正方形,其角点位于圆周上。画出连接正方形对角的斜线,由于对称性,它们将穿过圆心,形成 4 个相似的三角形。每个这样的三角形都是等腰三角形,并且在两条等长边在圆心相遇的地方有一个 π/2 弧度的角。因此,三角形的另外两个角必须相等,并且总和为 π/2 弧度,也就是说每个角的大小都必须是 π/4 弧度。我们知道这样的三角形是直角三角形,我们必须得出结论,π/2 弧度的角度确实是直角。
总之:可以使用几何论证来推断某些特殊情况下角度的大小。但是,一般而言,仅靠几何不足以确定任何任意三角形中未知角度的大小。为了解决这些问题,我们需要借助三角函数。
原则上,所有角度和三角函数都在单位圆上定义。在数学中,术语“单位”指的是任何长度的单个测量值。我们将在以后将从单位测量中获得的原理应用于更大(或更小)比例的问题。我们需要的函数都可以从内接于单位圆的三角形中推导出:它恰好是一个直角三角形。
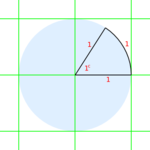
单位圆的中心点将设置在一个笛卡尔平面上,圆心位于平面的原点——点 (0,0)。因此我们的圆将被分成四个部分,或象限。
象限总是按逆时针方向计数,就像角速度 (omega)的默认旋转方向一样。现在我们在第一象限(即 x 轴和 y 轴分配正值的象限)中内接一个三角形,并让角度的一条边在 x 轴上,另一条边平行于 y 轴。(只需查看插图以进行澄清)。现在我们让斜边(始终为 1,即我们的单位圆的半径)逆时针旋转。你会注意到,当我们进入一个新的象限时,会形成一个新的三角形,不仅因为三角形的角度之和不能超过 180°,而且因为在二维平面上无法想象其他情况。




