三角学/爱好者/严谨的三角学

角度介绍

当两条直线相交时，就会形成一个角；交点称为顶点。我们可以将角视为两条直线相交处的楔形空间。请注意，如果将两条直线都通过交点延长，实际上就会有四个角。

角的大小是两条直线之间的旋转度数。我们必须旋转一条直线与另一条直线相交的次数越多，角度就越大。

假设您想精确测量两条直线之间的角度，以便告诉远处的朋友：以交点为圆心画一个圆，确保圆足够小以穿过两条直线，但又足够大以便您测量圆周上两条直线交点之间的距离。显然，此距离取决于圆的大小，但是只要您告诉您的朋友所用圆的半径和圆周上的长度，那么您的朋友就可以精确地重建该角度。

角度定义

角是由射线绕其端点旋转确定的。射线起始位置称为角的起始边。射线终止位置称为终边。射线的端点称为其顶点。正角是由逆时针旋转产生的。负角是由顺时针旋转产生的。

因此，一个角有四个部分：它的顶点、它的起始边、它的终边和它的旋转。

当一个角在笛卡尔坐标系中以其顶点位于原点，起始边为正 x 轴的方式绘制时，它被称为处于标准位置。

三角形定义

三角形是一个平面（扁平）形状，具有三条直边。三角形的每两条边之间都会形成一个角，一个三角形有三个角，因此得名三角形。所以一个三角形有三个直边和三个角。

如果你给我三个长度，我只能用它们做一个三角形，如果最长的长度小于另外两个长度的总和。三个不能构成三角形边的长度是你的身高，最近的树的高度，从树顶到太阳中心的距离。

三角比

角度不受线条长度的影响：角度在比例变换下是不变的，即

如果你把三角形变大，
但保持边之间的比例不变，
它的角度不会改变。

直角

一个特别重要的角是直角：正方形或矩形的每个角处的角。一个矩形总是可以通过从矩形的一个角到对面角画一条线来分成两个三角形。

每个直角三角形都是半个矩形也是真的。

一个矩形有四条边；它们通常有两种不同的长度：两条长边和两条短边。（所有边都相等的矩形是正方形。）当我们将矩形分成两个直角三角形时，每个三角形都具有矩形中的长边和短边，以及分割线的副本。

因此，直角三角形的面积是其分割成的矩形面积的一半。观察一个直角三角形，我们可以知道该矩形的长边和短边是什么；它们是直角相交的边，即线段。完整矩形的面积是长边乘以短边。因此，直角三角形的面积减半。

直角三角形和测量

可以使用以下过程仅使用圆（可以用圆规绘制）和直线来平分任何角度

将角的顶点称为 O。以 O 为圆心画一个圆。
标记圆与每条射线的交点。将这些点称为 A 和 B。
以 A 和 B 为圆心画两个半径相等的圆，但确保这些半径足够大以使圆在两点相交。一个确保这样做的方法是画线段 AB，并将圆的半径设为该线段的长度。在图中，圆 A 和圆 B 显示为圆的近一半部分。
标记这两个圆的交点，并将这两个点用一条线连接起来。这条线平分了原始角。

关于这条线平分角的证明可以在《几何原本》第一卷命题 9中找到。

给定一个直角，我们可以用这个过程无限地分割这个直角，以形成任何二进制分数（即， ${\frac {1}{2^{n}}},n\in \mathbb {Z}$ ，例如 ${\frac {1}{2}},{\frac {1}{4}},{\frac {1}{8}},{\frac {1}{16}},{\frac {1}{32}}...$ ）。因此，我们可以用直角来测量任何角度。也就是说，一个测量系统，其中直角的大小被认为是1。

弧度制的介绍

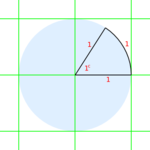
当然，也可以从不同的角度开始，并将其分成两个相等的角。我们可以认为半圆形成的角度为“1”，或全圆形成的角度为“1”。

如果我们选择以下奇怪的角度作为“1”，三角学将得到简化。

1. 画一个圆，并标记半径。
2. 从半径与圆周相交的点开始，沿圆周测量一个半径长度，并沿逆时针方向标记此点。
3. 从这个标记点画一条线到圆心。
4. 这样形成的角度在三角学中被认为是1；为了告诉你的朋友你使用的是这种方法，你会说“用弧度测量”。

理解弧度的三条边

为了说明弧度的三条边是如何相互关联的，尝试以下思维实验。

1. 假设你有一根绳子，它的长度正好等于圆的半径。
2. 假设你在同一个圆内画了一个弧度。弧度有3个点。一个点是圆心，另外两个点是在圆周上弧度的两条边与圆相交的地方。
3. 将绳子的一端固定在弧度与圆周相交的其中一个点上。
4. 从你上面步骤2中选择的那一点开始，用绳子的另一端沿着圆周追踪圆，朝弧度与圆周相交的第二个点移动，直到绳子被拉紧。
5. 你会看到绳子的末端超过了第二个点。
6. 这是因为绳子现在是一条直线。然而，弧度用一条弧作为第三边，而不是一条直线。尽管弧度有三个相等的边，但弧的曲线会导致弧度与圆周相交的两个点比它们到三角形第三个点的距离更近，在本例中，这个点是圆心。
7. 现在，在绳子仍然拉紧的情况下，找到绳子的中点，然后将其拉到圆周上，同时让绳子的末端沿着圆周移动。绳子的末端现在更靠近第二个点了，因为绳子的路径更靠近圆周的路径。
8. 我们可以通过将绳子的每个新部分都分成一半，并将其拉向圆周，不断改进绳子路径与圆周路径的匹配度。

弧度会受其圆的大小影响吗？也许使用大圆的半径会产生与使用小圆的半径不同的角度。答案是否定的。

使用什么大小的圆来测量弧度有关系吗？也许使用大圆的半径会产生与使用小圆的半径不同的角度。答案是否定的。

回顾我们上面小节中的弧度和圆。在第一个圆里面画另一个圆，与第一个圆有相同的圆心，但半径只有一半。你会看到你在较小的圆内创建了一个新的弧度，它与较大圆内的弧度具有相同的角度。我们知道，两个弧度从圆心发出的两条边等于它们各自圆的半径。我们还知道，较大圆内弧度的第三边（弧）也等于较大圆的半径。但是我们如何知道较小圆内弧度的第三边（沿着较小圆圆周的弧）等于较小圆的半径？为了弄清楚为什么我们知道较小圆弧度的第三边等于它的半径，我们首先将每个弧度与圆相交的两个点彼此连接起来。这样一来，你就创建了两个等腰三角形（有两个相等边和两个相等角的三角形）。

等腰三角形有两个相等的角和两个相等的边。如果你知道任何等腰三角形的一个角和构成这个角的两条边的长度，那么你可以很容易地推断出等腰三角形的其余特征。例如，如果等腰三角形的两条等距边相交形成一个等于 40^o 的角，那么你知道剩下的两个角都必须等于 70º。由于我们知道我们两个等腰三角形的等距边构成了我们已知的角，那么我们可以推断出我们两个弧度（当转换为具有直线的等腰三角形时）具有相同的第二个和第三个角。我们还知道，具有相同角度的三角形，无论它们的大小如何，它们的边长之比都是恒定的。例如，我们可以推断出，如果我们知道一个等腰三角形的边长为 1 米 × 2 米 × 2 米，那么一个具有相同角度的等腰三角形的边长将为 2 米 × 4 米 × 4 米。因此，在我们的例子中，由较小的第二个圆形成的等腰三角形的第三边将正好等于由较大圆创建的等腰三角形的第三边的一半。两个具有相同角度的三角形的边长之比，也存在于具有相同圆心的两个圆的半径和周长之间——它们将具有完全相同的比率。因此，在我们的例子中，由于我们第二个较小圆的半径正好是较大圆的一半，因此较小圆弧度相交的两个点之间的圆周（我们已经证明是较大圆上两个相似点之间距离的一半）将具有完全相同的比率。就是这样——圆的大小无关紧要。

用弧度测量角度

一旦我们有了1弧度的角度，我们就可以像处理直角一样将其分割成二进制分数，从而得到大量的已知角度，用来测量未知角度。量角器是一种使用这种技术来近似测量角度的设备。用量角器测量角度的方法：将量角器的标记中心放置在要测量的角度的顶点上，将量角器右侧的零弧度线与角度的一条边对齐，然后读出角度的另一条边与量角器边缘相交的位置。量角器通常是透明的，上面画有角度线，以帮助你测量由短线形成的角度：这是允许的，因为角度不取决于形成它们的线的长度。

如果我们同意用弧度测量角度，那么了解一些易于定义的角度的大小将很有用。当然，我们可以简单地画出角度，然后用量角器非常精确地测量它们，尽管仍然是近似的：但是，那样我们就会是在做物理，而不是数学。

圆的周长与其半径之比定义为 2π，其中π 是一个不变量，与圆的大小无关，上述论据证明了这一点。因此，如果我们沿圆的圆周从圆周上的一个给定点移动 2π 个半径，我们将回到起点。我们必须得出结论，圆周上绕一圈形成的角度为 2π 弧度。同样，绕圆半圈将是 π 弧度。想象一下，沿着对称轴将一个圆对折：形成的折痕将是一条直径，即穿过圆心的直线。因此，一条直线的角度大小为 π 弧度。

将半圆对折再对折，得到一个四分之一圆，因此它的角度必须是 π/2 弧度。四分之一圆是直角吗？为了说明它是直角：画一个正方形，它的四个角点都在圆周上。画出连接正方形对角线的线段，由于对称性，这些线段将穿过圆心，形成 4 个相似三角形。每个三角形都是等腰三角形，在圆心处两条等长边相交，形成的角度为 2π/4 = π/2 弧度。因此，三角形的另外两个角必须相等，并且和为 π/2 弧度，也就是说，每个角的大小必须为 π/4 弧度。我们知道这样的三角形是直角三角形，因此我们可以得出结论，π/2 弧度角确实是一个直角。

总结和附加说明

总之，我们可以利用几何论证来推断特定条件下某些角度的大小。然而，一般情况下，仅仅依靠几何学不足以确定任意三角形中未知角度的大小。为了解决这类问题，我们需要三角函数的帮助。

原则上，所有角度和三角函数都定义在单位圆上。数学中“单位”一词指代任何长度的单个度量。稍后，我们将把从单位度量中学到的原理应用到更大（或更小）比例的问题中。我们需要的全部函数都可以从内接于单位圆的三角形中推导出来：它恰好是一个直角三角形。

单位圆的圆心将被设置在笛卡尔平面上，圆心位于平面的原点——点 (0,0)。因此，我们的圆将被分成四个部分，或象限。

象限总是逆时针计数，这也是角速度 $\omega$ (omega) 的默认旋转方向。现在我们在第一象限（即 x 轴和 y 轴都被赋予正值的象限）内内接一个三角形，让角度的一条边在 x 轴上，另一条边平行于 y 轴。（只要看看图示，就能弄清楚）。现在我们让斜边（始终为 1，即我们单位圆的半径）逆时针旋转。你会注意到，当我们进入一个新的象限时，会形成一个新的三角形，这不仅是因为三角形内角和不能超过 180°，而且因为在二维平面上无法想象其他情况。