A-level 物理（进阶物理）/简谐运动

当作用于物体的力与物体的位移成正比且方向相反时，就会发生简谐运动。例如，弹簧上的质量和摆锤，它们会反复地来回“弹跳”。在数学上，这可以写成

$F=-kx$ ,

其中 F 是力，x 是位移，k 是一个正常数。这与胡克定律完全相同，胡克定律指出，弹簧末端的物体上的力 F 等于 -kx，其中 k 是弹簧常数。由于 F = ma，而加速度是位移对时间 t 的二阶导数

$m{\frac {d^{2}x}{dt^{2}}}=-kx$

${\frac {d^{2}x}{dt^{2}}}={\frac {-kx}{m}}$

这个二阶微分方程的解是

$x=A\cos {\omega t}$ ,

其中 A 是最大位移，ω 是物体的“角速度”。推导过程见这里，因为对于那些以前没有接触过复数的人来说，它看起来会非常可怕。需要注意的是，这个解在给定不同的起始条件后，会变成

$x=A\sin {\omega t}$ ,

角速度

圆周运动中的角速度是角变化率。它以弧度/秒为单位。由于 2π 弧度相当于周期 T 内的一次完整旋转

$\omega ={\frac {2\pi }{T}}=2\pi f$

如果我们将它代入简谐运动中位移的方程

$x=A\cos {2\pi ft}$

方程中包含角速度的原因是，简谐运动与圆周运动非常相似。如果你从侧面观察一个物体绕圆圈运动，它看起来就像简谐运动。我们已经注意到，弹簧上的质量会发生简谐运动。下图显示了圆周运动和简谐运动之间的相似性

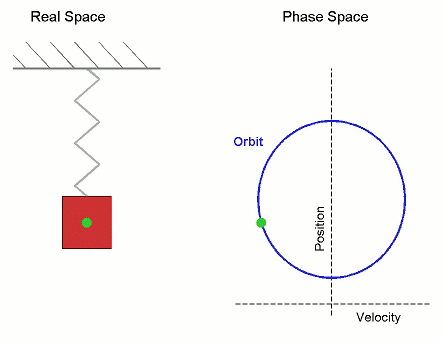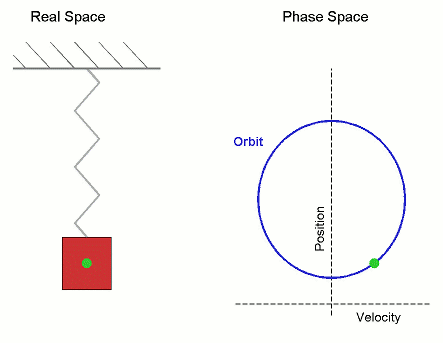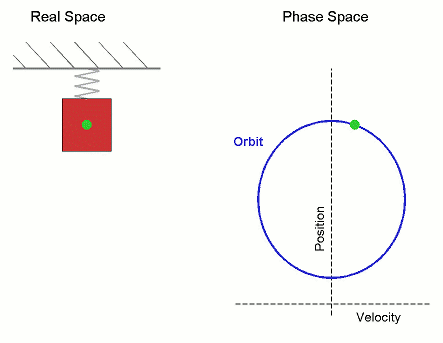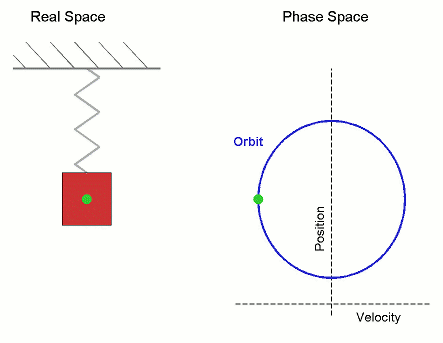
振荡的周期是指重复运动模式一次所需的时间。一般来说

$T={\frac {2\pi }{\omega }}$

但是，根据振荡的类型，ω 的值会发生变化。对于弹簧上的质量

$\omega ={\sqrt {\frac {k}{m}}}$

对于摆锤

$\omega ={\sqrt {\frac {g}{l}}}$ ,

其中 g 是重力场强，l 是绳子的长度。通过代入，我们可以得到以下表格

振荡类型	弹簧	摆锤
角速度	${\sqrt {\frac {k}{m}}}$	${\sqrt {\frac {g}{l}}}$
周期	$2\pi {\sqrt {\frac {m}{k}}}$	$2\pi {\sqrt {\frac {l}{g}}}$

简谐振子的位移是

$x=A\cos {\omega t}$

速度是位移变化率，所以

$v={\frac {dx}{dt}}=-A\omega \sin {\omega t}$

加速度是速度变化率，所以

$a={\frac {dv}{dt}}={\frac {d^{2}x}{dt^{2}}}=-A\omega ^{2}cos{\omega t}=-\omega ^{2}x$

1. 一个 10 牛顿的重物使弹簧伸长 5 厘米。再添加一个 10 牛顿的重物，弹簧又伸长了 5 厘米。弹簧的弹性系数是多少？

2. 将弹簧带到外太空，用两个重物将其拉伸 10 厘米。它的振动周期是多少？

3. 1 秒后，弹簧上作用着什么力？力的方向是什么？

4. 一个摆的振动频率是 0.5 赫兹。摆的长度是多少？

5. 下图显示了简谐振子的位移。绘制出它的速度、动量、加速度和作用在其上的力的图。

6. 只有当摆的振动角度很小时，它才能被建模为简谐振子。这是为什么？