抽象代数/群论/同态

我们终于要进入理论的核心部分了。在本节中，我们将研究群之间的结构保持映射。这项研究将开启新的途径，并为我们提供大量的新的定理。

到目前为止，我们一直在“元素级”研究群。由于我们现在即将退一步，在“同态级”研究群，读者应该预期从本节开始抽象程度会突然增加。我们将尝试通过始终在这一节中保留一只脚在“元素级”，来帮助读者适应这种变化。

从现在开始，符号$e_{G}$将表示群$G$中的单位元，除非另有说明。

群同态

定义 1：令$(G,*)$和$(H,\cdot )$为群。从$G$到$H$的同态是一个函数$\phi \,:\,G\rightarrow H$，使得对于所有$g_{1},g_{2}\in G$，

$\phi (g_{1}*g_{2})=\phi (g_{1})\cdot \phi (g_{2})$.

因此，同态保持群结构。我们在这里包含了乘法符号，以明确说明左侧的乘法发生在$G$中，右侧的乘法发生在$H$中。

我们已经看到，本节与之前的章节不同。到目前为止，除了子群之外，我们每次都只处理一个群。不再如此了！让我们首先从推导出定义的一些基本且直接的结果开始。

定理 2：令$G,H$为群，$\phi \,:\,G\rightarrow H$为同态。则$\phi (e_{G})=e_{H}$。换句话说，单位元映射到单位元。

证明：设$g\in G$。那么，$\phi (g)=\phi (e_{G}g)=\phi (e_{G})\phi (g)$，这意味着$\phi (e_{G})$是$H$中的单位元，证明了该定理。∎

定理 3：设$G,H$为群，$\phi \,:\,G\rightarrow H$为同态。那么对于任意$g\in G$，$\phi (g^{-1})=\phi (g)^{-1}$。换句话说，逆元被映射到逆元。

证明：设$g\in G$。那么$e_{H}=\phi (e_{G})=\phi (gg^{-1})=\phi (g)\phi (g^{-1})$，这意味着$\phi (g^{-1})=\phi (g)^{-1}$，如需证明。∎

定理 4：设$G,G^{\prime }$为群，$\phi \,:\,G\rightarrow G^{\prime }$为同态，并设$H$为$G$的子群。那么$\phi (H)=\{\phi (h)\mid h\in H\}$是$G^{\prime }$的子群。

证明：设$h_{1},h_{2}\in H$。则$\phi (h_{1}),\phi (h_{2})\in \phi (H)$，且$\phi (h_{1})\phi (h_{2})^{-1}=\phi (h_{1})\phi (h_{2}^{-1})=\phi (h_{1}h_{2}^{-1})$。由于$h_{1}h_{2}^{-1}\in H$，$\phi (h_{1})\phi (h_{2})^{-1}=\phi (h_{1}h_{2}^{-1})\in \phi (H)$，所以$\phi (H)$是$G^{\prime }$的子群。∎

定理 5：设$G,G^{\prime }$为群，$\phi \,:\,G\rightarrow G^{\prime }$为同态，且$H^{\prime }$为$G^{\prime }$的子群。则$\phi ^{-1}(H^{\prime })=\{g\in G\mid \phi (g)\in H^{\prime }\}$是$G$的子群。

证明：设$g_{1},g_{2}\in \phi ^{-1}(H^{\prime })$。则$\phi (g_{1}),\phi (g_{2})\in H^{\prime }$，并且由于$H^{\prime }$是子群，$\phi (g_{1})\phi (g_{2})^{-1}=\phi (g_{1})\phi (g_{2}^{-1})=\phi (g_{1}g_{2}^{-1})\in H^{\prime }$。但是，$g_{1}g_{2}^{-1}\in \phi ^{-1}(H^{\prime })$，因此$\phi ^{-1}(H^{\prime })$是$G$的子群。∎

从定理4和定理5可以看出，同态保持子群。因此，我们可以期望通过找到合适的同态到$G$来了解群$G$的子群结构。

特别是，每个同态$\phi \,:\,G\rightarrow G^{\prime }$都与两个重要的子群相关联。

定义 6：如果同态是双射的，并且其逆也是一个同态，则称该同态为同构。如果两个群之间存在同构，则称这两个群为同构，我们用$G\approx H$表示“$G$与$H$同构”。

定理 7：双射同态是同构。

证明：设$G,H$是群，并设$\phi \,:\,G\rightarrow H$是一个双射同态。我们必须证明其逆$\phi ^{-1}$也是一个同态。设$h_{1},h_{2}\in H$。那么存在唯一的$g_{1},g_{2}\in G$使得$\phi (g_{1})=h_{1}$ 以及 $\phi (g_{2})=h_{2}$。那么我们有$\phi (g_{1}g_{2})=h_{1}h_{2}$，因为$\phi$是一个同态。现在将$\phi ^{-1}$应用于所有等式。我们得到$\phi ^{-1}(h_{1})=g_{1}$，$\phi ^{-1}(h_{2})=g_{2}$ 以及 $\phi ^{-1}(h_{1}h_{2})=g_{1}g_{2}=\phi ^{-1}(h_{1})\phi ^{-1}(h_{2})$，因此$\phi ^{-1}$是一个同态，从而$\phi$是一个同构。∎

定义 8：设$G,G^{\prime }$是群。一个同态，它将$G$中的每个元素都映射到$e^{\prime }\in G^{\prime }$，称为平凡同态（或零同态），记为$0_{GG^{\prime }}\,:\,G\rightarrow G^{\prime }$

定义 9：设$H$是群$G$的一个子群。则由$i(h)=h$给出的同态$i\,:\,H\rightarrow G$称为$H$到$G$的包含映射。设$G^{\prime }$是一个与群$G$的一个子群$H$同构的群。则由$i^{\prime }(g^{\prime })=\phi (g^{\prime })$给出的同构$\phi \,:\,G^{\prime }\rightarrow H$诱导了一个单射同态$i^{\prime }\,:\,G^{\prime }\rightarrow G$，称为$G^{\prime }$到$G$的嵌入。显然，$i^{\prime }=i\circ \phi$。

定义 10：设$G,G^{\prime }$ 为群，且$\phi \,:\,G\rightarrow G^{\prime }$ 为同态。那么我们定义以下子群

i) $\ker \,\phi =\{g\in G\mid \phi (g)=e^{\prime }\}\leq G$，称为$\phi$的核，以及

ii) $\mathrm {im} \,\phi =\{g^{\prime }\in G^{\prime }\mid (\exists g\in G)\phi (g)=g^{\prime }\}\leq G^{\prime }$，称为$\phi$的像。

定理 11：同态的复合是同态。

证明：设$G,H,K$ 为群，且$\phi \,:\,G\rightarrow H$ 和$\psi \,:\,H\rightarrow K$ 为同态。那么$\psi \circ \phi \,:\,G\rightarrow K$ 是一个函数。我们必须证明它是一个同态。设$g,h\in G$。那么$\psi \circ \phi (gh)=\psi (\phi (gh))=\psi (\phi (g)\phi (h))=\psi (\phi (g))\psi (\phi (h))=\psi \circ \phi (g)\psi \circ \phi (h)$，因此$\psi \circ \phi$ 确实是一个同态。 ∎

定理 12：同态的复合是结合的。

证明：这很明显，因为同态是函数，而函数的复合是结合的。 ∎

推论 13：同构的复合是同构。

证明：这根据定理 11 和双射的复合是双射而显而易见。 ∎

定理 14：设$G,H$ 为群，且$\phi \,:\,G\rightarrow H$ 为一个同态。则$\phi$ 是单射当且仅当$\ker \,\phi =\{e\}\subseteq G$。

证明：假设$\ker \,\phi =\{e\}$ 且 $g_{1},g_{2}\in G$。则 $\phi (g_{1})=\phi (g_{2})\,\Leftrightarrow \phi (g_{1})\phi (g_{2})^{-1}=\phi (g_{1}g_{2}^{-1})=e_{H}$，这意味着 $g_{1}g_{2}^{-1}\in \ker \,\phi$。但根据假设，则 $g_{1}g_{2}^{-1}=e\,\Leftrightarrow g_{1}=g_{2}$，因此 $\phi$ 是单射的。现在假设 $\ker \,\phi \neq \{e\}$ 且 $g\in G$。则存在另一个元素 $k\in \ker \,\phi$，使得 $k\neq e$。但随后 $\phi (g)=\phi (kg)$。由于 $g$ 和 $kg\neq g$ 都映射到 $\phi (g)=\phi (kg)$，$\phi$ 不是单射的，从而证明了该定理。∎

推论 15：包含映射是单射的。

证明：结果是直接的。由于对于所有$h\in H\leq G$，都有$i(h)=h$，我们有$i^{-1}(e)=\{e\}$。∎

可以看出核满足一个泛性质。下面的定理解释了这一点，但对于群的初等处理来说，它异常抽象，如果读者不能立即理解它，也不要担心。

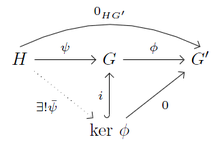显示核的泛性质的交换图。

定理 16：设$G,G^{\prime }$是群，$\phi \,:\,G\rightarrow G^{\prime }$是群同态。还设$H$是群，$\psi \,:\,H\rightarrow G$是同态，使得$\phi \circ \psi =0_{HG^{\prime }}$。还设$i\,:\,\ker \,\phi \rightarrow G$是$\ker \,\phi$到$G$的包含映射。则存在唯一的同态${\bar {\psi }}\,:\,H\rightarrow \ker \,\phi$，使得$\psi =i\circ {\bar {\psi }}$。

证明：由于$\phi \circ \psi =0_{HG^{\prime }}$，根据定义，我们必须有$\psi (H)\leq \ker \,\phi$，所以${\bar {\psi }}$ 存在。交换律$\psi =i\circ {\bar {\psi }}$ 然后迫使${\bar {\psi }}(h)=\psi (h)\in \ker \,\phi$，所以${\bar {\psi }}$ 是唯一的。 ∎

定义 17：交换图是函数网络的一种图示表示。交换性意味着当从一个对象到同一目标有多条函数复合路径时，这两条复合路径作为函数是相等的。例如，右侧的交换图描述了定理 16 中的情况。在本章关于群的交换图（或简称为图，我们不会展示不交换的图）中，所有函数都被隐式地假定为群同态。图中的单射通常用带钩的箭头强调。此外，满射通常用双头箭头强调。包含是单射这一点将在稍后证明。

注记 18：从右侧的交换图中，可以完全定义核，而无需引用元素。实际上，定理 16 将成为定义，而我们的定义 10 i) 将成为一个定理。本书不会探讨这种思路，但欢迎高级读者自行推导。

自同构群

在本小节中，我们将研究从一个群到其自身的同态。

定义 19：从一个群$G$到其自身的同态称为$G$的自同态。既是同态又是同构的自同态称为自同构。$G$的所有自同态的集合记为$\mathrm {End} (G)$，而$G$的所有自同构的集合记为$\mathrm {Aut} (G)$。

定理 20：$\mathrm {End} (G)$在同态的复合运算下是一个幺半群。此外，$\mathrm {Aut} (G)$是一个子幺半群，它也是一个群。

证明：我们只需要确认$\mathrm {End} (G)$是封闭的并且具有单位元，我们知道这是正确的。对于$\mathrm {Aut} (G)$，恒等同态$\mathrm {id} _{G}\,:\,G\rightarrow G$是一个同构，并且同构的复合也是同构。因此$\mathrm {Aut} (G)$是一个子幺半群。为了证明它是一个群，注意自同构的反自同构也是一个自同构，所以$\mathrm {Aut} (G)$确实是一个群。∎

带运算符的群

群的自同态可以被认为是该群上的一个一元运算符。这促使了以下定义

定义 21：设$G$是一个群，并且$\Omega \subset \mathrm {End} (G)$。那么对$(G,\Omega )$称为带运算符的群。$\Omega$称为运算符域，其元素称为$G$的同态。对于任何$\omega \in \Omega$，我们引入简写$\omega (g)=g^{\omega }$，对于所有$g\in G$。因此，$G$的同态是自同态这一事实可以这样表达：对于所有$a,b\in G$和$\omega \in \Omega$，$(ab)^{\omega }=a^{\omega }b^{\omega }$。

例 22：对于任何群$G$，对$(G,\emptyset )$显然是一个带运算符的群。

引理 23：设$(G,\Omega )$是一个带运算的群。则$\Omega$可以扩展到$\mathrm {End} (G)$的一个子幺半群$\Omega ^{\prime }$，使得$(G,\Omega ^{\prime })$的结构与$(G,\Omega )$相同。

证明：设$\Omega ^{\prime }$包含恒等自同态，并设$\Omega$是一个生成集。则$\Omega ^{\prime }$在复合运算下是封闭的，是一个幺半群。由于$\Omega ^{\prime }$的任何元素都可以表示为$\Omega$中元素的（可能为空的）复合，因此这两个结构是相同的。∎

在下文中，我们假设运算域始终为幺半群。如果不是，我们可以根据引理 23将其扩展为幺半群。

定义 24：设$(G,\Omega )$和$(H,\Omega )$是具有相同运算域的带运算的群。则同态$\phi \,:\,(G,\Omega )\rightarrow (H,\Omega )$是一个群同态$\phi \,:\,G\rightarrow H$，使得对于所有$\omega \in \Omega$和$g\in G$，我们有$\phi (g^{\omega })=\phi (g)^{\omega }$。

定义 25：设$(G,\Omega )$ 是一个带运算的群，$H$ 是 $G$ 的一个子群。则如果对于所有 $h\in H$ 和 $\omega \in \Omega$，都有 $h^{\omega }\in H$，则称 $H$ 为稳定子群（或$\Omega$-不变子群）。我们说 $H$服从 $G$ 的同态。在这种情况下，$(H,\Omega )$ 是一个带运算的子群。

例 26：设$V$ 是域 $F$ 上的一个向量空间。如果我们用 $V_{+}$ 表示其在加法下的阿贝尔群，则 $V=(V_{+},F)$ 是一个带运算的群，其中对于任何 $k\in F$ 和 $v\in V_{+}$，我们定义 $v^{k}=kv$。则稳定子群恰好是 $V$ 的线性子空间（证明这一点）。

习题

问题 1：证明不存在从$\mathbb {Z} _{5}$ 到 $S_{3}$ 的非平凡同态。