低音反射箱体可以改善扬声器系统的低频响应。 低音反射箱体也称为“通风箱设计”或“端口箱体设计”。 低音反射箱体包括一个箱体和环境之间的通风口或端口。 这种设计,正如人们从当代扬声器产品中看到的那样,如今仍然被广泛使用。 虽然低音反射箱体的构造相当简单,但其设计并不简单,需要适当的调整。 本参考重点介绍低音反射设计的技术细节。 可以在这里 找到一般扬声器信息。
在讨论低音反射箱体之前,了解更简单的密闭箱体系统性能非常重要。 正如其名称所示,密闭箱体系统将扬声器连接到一个密闭的箱体(除了一个用于平衡箱体内环境压力的微小泄漏)。 理想情况下,箱体将充当声学顺应元件,因为箱体内的空气被压缩和稀疏。 但是,通常情况下,箱体内会添加声学材料以减少驻波、消散热量以及其他原因。 这在声学集总元件模型中添加了一个阻抗元件。 箱体效应的非理想模型实际上添加了一个声学质量元件来完成图 1 中给出的串联集总元件电路。 有关密闭箱体设计的更多信息,请参阅密闭箱体低音炮设计 页面。
图 1. 密闭箱体的声学电路。
在低音反射箱体的情况下,会在结构中添加一个端口。 通常,端口是圆柱形的,并且在指向箱体外的端部带有法兰。 在低音反射箱体中,使用的声音学材料量通常远小于密闭箱体的情况,通常根本没有。 这允许空气自由地流过端口。 相反,更大的损耗来自箱体中的漏气。 通过这种设置,集总元件声学电路具有如下所示的形状。
图 2. 低音反射箱体的声学电路。
在此图中, Z R A D {\displaystyle Z_{RAD}} M A P {\displaystyle M_{AP}} C A B {\displaystyle C_{AB}} R A L {\displaystyle R_{AL}} M A P {\displaystyle M_{AP}} M A B {\displaystyle M_{AB}} 附录 B 中。
重要的是要注意 M A P {\displaystyle M_{AP}} C A B {\displaystyle C_{AB}} 点击此处了解更多信息 )。在物理上,端口充当共鸣器的“颈部”,而外壳充当“腔体”。在本例中,共鸣器直接由活塞驱动腔体,而不是典型的亥姆霍兹共鸣器通过“颈部”驱动。然而,相同的共振行为仍然在外壳共振频率 f B {\displaystyle f_{B}} 1 / Z {\displaystyle 1/Z} f B {\displaystyle f_{B}}
图 3. 扬声器振膜和音圈看到的阻抗。
扬声器的性能首先通过其速度响应进行测量,这可以直接从系统的等效电路中找到。由于大多数扬声器设计的目标是改善低音响应(将高频产生留给高音扬声器),因此将尽可能多地进行低频近似以简化分析。首先,音圈的电感 L E {\displaystyle {\it {L_{E}}}} ω ≪ R E / L E {\displaystyle \omega \ll R_{E}/L_{E}} L E {\displaystyle {\it {L_{E}}}} R E {\displaystyle {\it {R_{E}}}} Ω {\displaystyle \Omega }
另一个近似涉及辐射阻抗 Z R A D {\displaystyle {\it {Z_{RAD}}}}
Z R A D = ρ 0 c π a 2 [ ( 1 − J 1 ( 2 k a ) k a ) + j H 1 ( 2 k a ) k a ] {\displaystyle Z_{RAD}={\frac {\rho _{0}c}{\pi a^{2}}}\left[\left(1-{\frac {J_{1}(2ka)}{ka}}\right)+j{\frac {H_{1}(2ka)}{ka}}\right]} 其中 J 1 ( x ) {\displaystyle J_{1}(x)} H 1 ( x ) {\displaystyle H_{1}(x)} ka 值,
J 1 ( 2 k a ) ≈ k a {\displaystyle J_{1}(2ka)\approx ka} 和
H 1 ( 2 k a ) ≈ 8 ( k a ) 2 3 π {\displaystyle H_{1}(2ka)\approx {\frac {8(ka)^{2}}{3\pi }}} ⇒ Z R A D ≈ j 8 ρ 0 ω 3 π 2 a = j M A 1 {\displaystyle \Rightarrow Z_{RAD}\approx j{\frac {8\rho _{0}\omega }{3\pi ^{2}a}}=jM_{A1}}
因此,扬声器上的低频阻抗用声学质量表示 M A 1 {\displaystyle M_{A1}} R E {\displaystyle R_{E}} M M D {\displaystyle M_{MD}} C M S {\displaystyle C_{MS}} R M S {\displaystyle R_{MS}} Thiele-Small 参数)被转换为其声学等效值。所有参数的所有转换都在 附录 A 中给出。然后,串联质量, M A D {\displaystyle M_{AD}} M A 1 {\displaystyle M_{A1}} M A B {\displaystyle M_{AB}} M A C {\displaystyle M_{AC}}
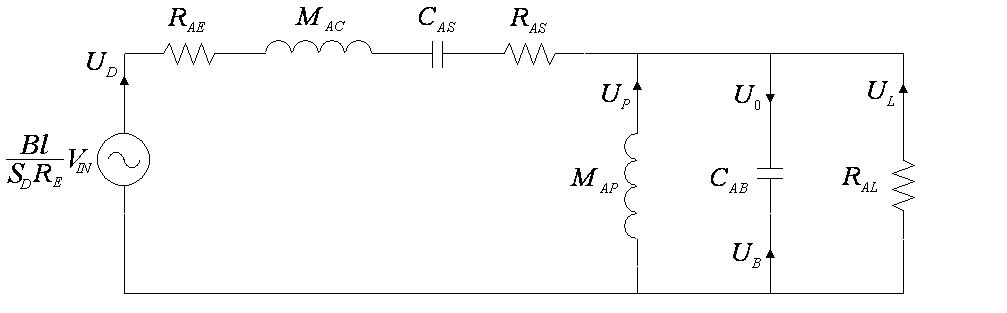
图 4. 低频等效声学电路
与密封箱体分析不同,有多个声速源向外部环境辐射。因此,振膜声速, U D {\displaystyle U_{D}} U 0 = U D + U P + U L {\displaystyle U_{0}=U_{D}+U_{P}+U_{L}} U 0 {\displaystyle U_{0}} U B = − U 0 {\displaystyle U_{B}=-U_{0}} V I N {\displaystyle V_{IN}} U 0 {\displaystyle U_{0}}
为了使方程式更容易理解,将多个参数组合起来形成其他参数名称。首先, ω B {\displaystyle \omega _{B}} ω S {\displaystyle \omega _{S}}
ω B = 1 M A P C A B {\displaystyle \omega _{B}={\frac {1}{\sqrt {M_{AP}C_{AB}}}}} ω S = 1 M A C C A S {\displaystyle \omega _{S}={\frac {1}{\sqrt {M_{AC}C_{AS}}}}}
根据推导的性质,定义参数 ω 0 {\displaystyle \omega _{0}} h ,亥姆霍兹调谐比为
ω 0 = ω B ω S {\displaystyle \omega _{0}={\sqrt {\omega _{B}\omega _{S}}}} h = ω B ω S {\displaystyle h={\frac {\omega _{B}}{\omega _{S}}}}
一个被称为顺应性比 或体积比 的参数, α {\displaystyle \alpha }
α = C A S C A B = V A S V A B {\displaystyle \alpha ={\frac {C_{AS}}{C_{AB}}}={\frac {V_{AS}}{V_{AB}}}} 其他参数组合起来形成所谓的品质因数
Q L = R A L C A B M A P {\displaystyle Q_{L}=R_{AL}{\sqrt {\frac {C_{AB}}{M_{AP}}}}} Q T S = 1 R A E + R A S M A C C A S {\displaystyle Q_{TS}={\frac {1}{R_{AE}+R_{AS}}}{\sqrt {\frac {M_{AC}}{C_{AS}}}}}
这种表示法允许对最终传递函数 [1] 进行更简单的表达
U 0 V I N = G ( s ) = ( s 3 / ω 0 4 ) ( s / ω 0 ) 4 + a 3 ( s / ω 0 ) 3 + a 2 ( s / ω 0 ) 2 + a 1 ( s / ω 0 ) + 1 {\displaystyle {\frac {U_{0}}{V_{IN}}}=G(s)={\frac {(s^{3}/\omega _{0}^{4})}{(s/\omega _{0})^{4}+a_{3}(s/\omega _{0})^{3}+a_{2}(s/\omega _{0})^{2}+a_{1}(s/\omega _{0})+1}}} 其中
a 1 = 1 Q L h + h Q T S {\displaystyle a_{1}={\frac {1}{Q_{L}{\sqrt {h}}}}+{\frac {\sqrt {h}}{Q_{TS}}}} a 2 = α + 1 h + h + 1 Q L Q T S {\displaystyle a_{2}={\frac {\alpha +1}{h}}+h+{\frac {1}{Q_{L}Q_{TS}}}} a 3 = 1 Q T S h + h Q L {\displaystyle a_{3}={\frac {1}{Q_{TS}{\sqrt {h}}}}+{\frac {\sqrt {h}}{Q_{L}}}}
可以证明[2],对于 k a < 1 / 2 {\displaystyle ka<1/2} a 表示扬声器的半径。对于空气中的 15 英寸直径扬声器,此低频极限约为 150 赫兹。对于较小的扬声器,此极限会增加。此极限主导忽略 L E {\displaystyle L_{E}} Z R A D {\displaystyle Z_{RAD}} M A 1 {\displaystyle M_{A1}}
在此极限内,扬声器发出体积速度 U 0 {\displaystyle U_{0}} U 0 {\displaystyle U_{0}}
p ( r ) ≃ j ω ρ 0 U 0 e − j k r 4 π r {\displaystyle p(r)\simeq j\omega \rho _{0}U_{0}{\frac {e^{-jkr}}{4\pi r}}}
为了简化分析,可以简单地令 r = 1 {\displaystyle r=1}
p V I N = ρ 0 s 4 π U 0 V I N = ρ 0 B l 4 π S D R E M A S H ( s ) {\displaystyle {\frac {p}{V_{IN}}}={\frac {\rho _{0}s}{4\pi }}{\frac {U_{0}}{V_{IN}}}={\frac {\rho _{0}Bl}{4\pi S_{D}R_{E}M_{A}S}}H(s)}
其中 H ( s ) = s G ( s ) {\displaystyle H(s)=sG(s)} | H ( s ) | 2 {\displaystyle |H(s)|^{2}} H ( s ) {\displaystyle H(s)}
| H ( s ) | 2 = Ω 8 Ω 8 + ( a 3 2 − 2 a 2 ) Ω 6 + ( a 2 2 + 2 − 2 a 1 a 3 ) Ω 4 + ( a 1 2 − 2 a 2 ) Ω 2 + 1 {\displaystyle |H(s)|^{2}={\frac {\Omega ^{8}}{\Omega ^{8}+\left(a_{3}^{2}-2a_{2}\right)\Omega ^{6}+\left(a_{2}^{2}+2-2a_{1}a_{3}\right)\Omega ^{4}+\left(a_{1}^{2}-2a_{2}\right)\Omega ^{2}+1}}} Ω = ω ω 0 {\displaystyle \Omega ={\frac {\omega }{\omega _{0}}}}
这也隐含地忽略了 | H ( s ) | {\displaystyle |H(s)|}
确定理想参数的一种流行方法是通过使用对齐方式。对齐方式的概念基于滤波器理论。滤波器开发是一种选择传递函数的极点(以及可能的零点)以满足特定设计标准的方法。这些标准是幅度平方传递函数的期望属性,在本例中为 | H ( s ) | 2 {\displaystyle |H(s)|^{2}} | H ( s ) | 2 {\displaystyle |H(s)|^{2}} | H ( s ) | 2 {\displaystyle |H(s)|^{2}}
有许多不同类型的滤波器设计,每种设计都有与之相关的权衡。然而,这种设计受到 | H ( s ) | 2 {\displaystyle |H(s)|^{2}} s = 0。因此,只有那些产生仅有极点的低通滤波器的滤波器设计方法才是可接受的方法。从传统的算法集中,只有巴特沃斯和切比雪夫低通滤波器只有极点。此外,还可以使用另一种称为准巴特沃斯滤波器的滤波器,它具有与巴特沃斯滤波器相似的属性。这三种算法都相当简单,因此它们是最受欢迎的。当这些低通滤波器转换为高通滤波器时, s → 1 / s {\displaystyle s\rightarrow 1/s} s 8 {\displaystyle s^{8}}
有关滤波器理论和这些关系的更多详细信息,可以在许多资源中找到,包括 [5]。
巴特沃斯算法旨在获得最大程度平坦 的通带。由于函数的斜率对应于它的导数,因此平坦的函数将具有等于零的导数。由于尽可能平坦的通带是最佳的,因此理想函数在s = 0 处将具有尽可能多的等于零的导数。当然,如果所有导数都等于零,那么该函数将是一个常数,它不执行任何过滤。
通常,检查所谓的损耗函数 更好。损耗是增益的倒数,因此
| H ^ ( s ) | 2 = 1 | H ( s ) | 2 {\displaystyle |{\hat {H}}(s)|^{2}={\frac {1}{|H(s)|^{2}}}}
损耗函数可用于实现所需特性,然后从损耗函数中恢复所需增益函数。
现在,应用所需的巴特沃斯特性,即最大通带平坦度,损耗函数只是一个多项式,其导数在s = 0 处等于零。同时,原始多项式必须是八次方(产生一个四阶函数)。但是,如果 [3]
| H ^ ( Ω ) | 2 = 1 + Ω 8 ⇒ | H ( Ω ) | 2 = 1 1 + Ω 8 {\displaystyle |{\hat {H}}(\Omega )|^{2}=1+\Omega ^{8}\Rightarrow |H(\Omega )|^{2}={\frac {1}{1+\Omega ^{8}}}}
使用高通变换 Ω → 1 / Ω {\displaystyle \Omega \rightarrow 1/\Omega }
| H ( Ω ) | 2 = Ω 8 Ω 8 + 1 {\displaystyle |H(\Omega )|^{2}={\frac {\Omega ^{8}}{\Omega ^{8}+1}}}
定义 Ω = ω / ω 3 d B {\displaystyle \Omega =\omega /\omega _{3dB}} Ω = 1 ⇒ | H ( s ) | 2 = 0.5 {\displaystyle \Omega =1\Rightarrow |H(s)|^{2}=0.5} | H ( s ) | 2 {\displaystyle |H(s)|^{2}} ω 3 d B = ω 0 {\displaystyle \omega _{3dB}=\omega _{0}}
a 1 = a 3 = 4 + 2 2 {\displaystyle a_{1}=a_{3}={\sqrt {4+2{\sqrt {2}}}}} a 2 = 2 + 2 {\displaystyle a_{2}=2+{\sqrt {2}}}
与巴特沃斯对齐相比,准巴特沃斯对齐没有那么明确的算法。“准巴特沃斯”这个名称源于这些响应的传递函数与巴特沃斯函数非常相似,通常在分母中添加了项。这将在下面进行说明。虽然有很多类型的准巴特沃斯对齐,但最简单、最流行的是三阶对齐(QB3)。下面显示了 QB3 幅度平方响应与四阶巴特沃斯的比较。
| H Q B 3 ( ω ) | 2 = ( ω / ω 3 d B ) 8 ( ω / ω 3 d B ) 8 + B 2 ( ω / ω 3 d B ) 2 + 1 {\displaystyle \left|H_{QB3}(\omega )\right|^{2}={\frac {(\omega /\omega _{3dB})^{8}}{(\omega /\omega _{3dB})^{8}+B^{2}(\omega /\omega _{3dB})^{2}+1}}} | H B 4 ( ω ) | 2 = ( ω / ω 3 d B ) 8 ( ω / ω 3 d B ) 8 + 1 {\displaystyle \left|H_{B4}(\omega )\right|^{2}={\frac {(\omega /\omega _{3dB})^{8}}{(\omega /\omega _{3dB})^{8}+1}}}
请注意,情况 B = 0 {\displaystyle B=0}
图 5: 3 阶准巴特沃斯响应, 0.1 ≤ B ≤ 3 {\displaystyle 0.1\leq B\leq 3} 将系统响应 | H ( s ) | 2 {\displaystyle |H(s)|^{2}} | H Q B 3 ( s ) | 2 {\displaystyle |H_{QB3}(s)|^{2}}
B 2 = a 1 2 − 2 a 2 {\displaystyle B^{2}=a_{1}^{2}-2a_{2}} a 2 2 + 2 = 2 a 1 a 3 {\displaystyle a_{2}^{2}+2=2a_{1}a_{3}} a 3 = 2 a 2 {\displaystyle a_{3}={\sqrt {2a_{2}}}} a 2 > 2 + 2 {\displaystyle a_{2}>2+{\sqrt {2}}}
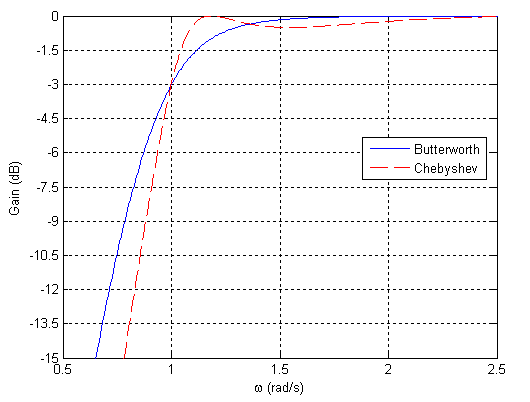
切比雪夫算法是巴特沃斯算法的替代方案。对于切比雪夫响应,最大平坦通带限制被放弃。现在,通带允许出现 *纹波* 或波动。这允许更陡峭的过渡或滚降发生。在这种类型的应用中,扬声器的低频响应可以扩展到超出巴特沃斯型滤波器所能达到的水平。下图显示了具有 0.5 dB 纹波的切比雪夫高通响应与具有相同 ω 3 d B {\displaystyle \omega _{3dB}}
图 6: 切比雪夫与巴特沃斯高通响应。
切比雪夫响应由 [4] 定义
| H ^ ( j Ω ) | 2 = 1 + ϵ 2 C n 2 ( Ω ) {\displaystyle |{\hat {H}}(j\Omega )|^{2}=1+\epsilon ^{2}C_{n}^{2}(\Omega )}
C n ( Ω ) {\displaystyle C_{n}(\Omega )}
C n ( Ω ) = { {\displaystyle C_{n}(\Omega )={\big \lbrace }} cos [ n cos − 1 ( Ω ) ] {\displaystyle \cos[n\cos ^{-1}(\Omega )]} | Ω | < 1 {\displaystyle |\Omega |<1}
cosh [ n cosh − 1 ( Ω ) ] {\displaystyle \cosh[n\cosh ^{-1}(\Omega )]} | Ω | > 1 {\displaystyle |\Omega |>1}
幸运的是,切比雪夫多项式满足一个简单的递归公式 [4]
C 0 ( x ) = 1 {\displaystyle C_{0}(x)=1} C 1 ( x ) = x {\displaystyle C_{1}(x)=x} C n ( x ) = 2 x C n − 1 − C n − 2 {\displaystyle C_{n}(x)=2xC_{n-1}-C_{n-2}}
有关切比雪夫多项式的更多信息,请参见 Wolfram Mathworld: 切比雪夫多项式 页面。
当将高通变换应用于 | H ^ ( j Ω ) | 2 {\displaystyle |{\hat {H}}(j\Omega )|^{2}}
| H ( j Ω ) | 2 = 1 + ϵ 2 1 + ϵ 2 C 4 2 ( 1 / Ω ) {\displaystyle |H(j\Omega )|^{2}={\frac {1+\epsilon ^{2}}{1+\epsilon ^{2}C_{4}^{2}(1/\Omega )}}}
参数 ϵ {\displaystyle \epsilon } 10 l o g [ 1 + ϵ 2 ] {\displaystyle 10{\rm {{log}[1+\epsilon ^{2}]}}} B 。使用 C n ( x ) {\displaystyle C_{n}(x)}
C 4 ( 1 Ω ) = 8 ( 1 Ω ) 4 − 8 ( 1 Ω ) 2 + 1 {\displaystyle C_{4}\left({\frac {1}{\Omega }}\right)=8\left({\frac {1}{\Omega }}\right)^{4}-8\left({\frac {1}{\Omega }}\right)^{2}+1}
将此方程应用于 | H ( j Ω ) | 2 {\displaystyle |H(j\Omega )|^{2}}
⇒ | H ( Ω ) | 2 = 1 + ϵ 2 64 ϵ 2 Ω 8 1 + ϵ 2 64 ϵ 2 Ω 8 + 1 4 Ω 6 + 5 4 Ω 4 − 2 Ω 2 + 1 {\displaystyle \Rightarrow |H(\Omega )|^{2}={\frac {{\frac {1+\epsilon ^{2}}{64\epsilon ^{2}}}\Omega ^{8}}{{\frac {1+\epsilon ^{2}}{64\epsilon ^{2}}}\Omega ^{8}+{\frac {1}{4}}\Omega ^{6}+{\frac {5}{4}}\Omega ^{4}-2\Omega ^{2}+1}}}
Ω = ω ω n {\displaystyle \Omega ={\frac {\omega }{\omega _{n}}}} ω n = ω 3 d B 2 2 + 2 + 2 2 + 1 ϵ 2 {\displaystyle \omega _{n}={\frac {\omega _{3dB}}{2}}{\sqrt {2+{\sqrt {2+2{\sqrt {2+{\frac {1}{\epsilon ^{2}}}}}}}}}}
因此,设计方程变为 [1]
ω 0 = ω n 64 ϵ 2 1 + ϵ 2 8 {\displaystyle \omega _{0}=\omega _{n}{\sqrt[{8}]{\frac {64\epsilon ^{2}}{1+\epsilon ^{2}}}}} k = tanh [ 1 4 sinh − 1 ( 1 ϵ ) ] {\displaystyle k=\tanh \left[{\frac {1}{4}}\sinh ^{-1}\left({\frac {1}{\epsilon }}\right)\right]} D = k 4 + 6 k 2 + 1 8 {\displaystyle D={\frac {k^{4}+6k^{2}+1}{8}}}
a 1 = k 4 + 2 2 D 4 , {\displaystyle a_{1}={\frac {k{\sqrt {4+2{\sqrt {2}}}}}{\sqrt[{4}]{D}}},} a 2 = 1 + k 2 ( 1 + 2 ) D {\displaystyle a_{2}={\frac {1+k^{2}(1+{\sqrt {2}})}{\sqrt {D}}}} a 3 = a 1 D [ 1 − 1 − k 2 2 2 ] {\displaystyle a_{3}={\frac {a_{1}}{\sqrt {D}}}\left[1-{\frac {1-k^{2}}{2{\sqrt {2}}}}\right]}
在已经介绍的所有方程中,自然会产生一个问题:“我应该选择哪一个?” 注意,系数 a 1 {\displaystyle a_{1}} a 2 {\displaystyle a_{2}} a 3 {\displaystyle a_{3}}
巴特沃斯对齐的通用指南侧重于 Q L {\displaystyle Q_{L}} Q T S {\displaystyle Q_{TS}} a 1 {\displaystyle a_{1}} a 2 {\displaystyle a_{2}} a 3 {\displaystyle a_{3}} Q L {\displaystyle Q_{L}} Q T S {\displaystyle Q_{TS}} h 和 α {\displaystyle \alpha } Q T S {\displaystyle Q_{TS}} Q L {\displaystyle Q_{L}}
如果无法满足巴特沃斯对齐的严格要求,则当 Q T S {\displaystyle Q_{TS}} B 允许在设计中具有更大的灵活性。
对于 Q T S {\displaystyle Q_{TS}}
除了这三种流行的对齐方式外,在开发能够操纵低音反射箱低频响应的新算法领域的研究还在继续。例如,已经开发出 5 阶准巴特沃斯对齐 [6]。另一个例子 [7] 应用根轨迹技术来实现结果。在现代高性能计算时代,其他研究人员将他们的工作重点放在创建可以修改以实现更平坦响应和更锐利滚降,或引入准纹波以提供超低音频率提升的计算机优化算法 [8]。
[1] Leach, W. Marshall, Jr. Introduction to Electroacoustics and Audio Amplifier Design . 2nd ed. Kendall/Hunt, Dubuque, IA. 2001.
[2] Beranek, L. L. Acoustics . 2nd ed. Acoustical Society of America, Woodbridge, NY. 1993.
[3] DeCarlo, Raymond A. “The Butterworth Approximation.” Notes from ECE 445. Purdue University. 2004.
[4] DeCarlo, Raymond A. “The Chebyshev Approximation.” Notes from ECE 445. Purdue University. 2004.
[5] VanValkenburg, M. E. Analog Filter Design . Holt, Rinehart and Winston, Inc. Chicago, IL. 1982.
[6] Kreutz, Joseph and Panzer, Joerg. "Derivation of the Quasi-Butterworth 5 Alignments." Journal of the Audio Engineering Society . Vol. 42, No. 5, May 1994.
[7] Rutt, Thomas E. "Root-Locus Technique for Vented-Box Loudspeaker Design." Journal of the Audio Engineering Society . Vol. 33, No. 9, September 1985.
[8] Simeonov, Lubomir B. and Shopova-Simeonova, Elena. "Passive-Radiator Loudspeaker System Design Software Including Optimization Algorithm." Journal of the Audio Engineering Society . Vol. 47, No. 4, April 1999.
名称
电气等效
机械等效
声学等效
音圈电阻
R E {\displaystyle R_{E}} R M E = ( B l ) 2 R E {\displaystyle R_{ME}={\frac {(Bl)^{2}}{R_{E}}}} R A E = ( B l ) 2 R E S D 2 {\displaystyle R_{AE}={\frac {(Bl)^{2}}{R_{E}S_{D}^{2}}}}
驱动器(扬声器)质量
见 C M E C {\displaystyle C_{MEC}}
M M D {\displaystyle M_{MD}} M A D = M M D S D 2 {\displaystyle M_{AD}={\frac {M_{MD}}{S_{D}^{2}}}}
驱动器(扬声器)悬挂顺性
L C E S = ( B l ) 2 C M S {\displaystyle L_{CES}=(Bl)^{2}C_{MS}} C M S {\displaystyle C_{MS}} C A S = S D 2 C M S {\displaystyle C_{AS}=S_{D}^{2}C_{MS}}
驱动器(扬声器)悬挂阻力
R E S = ( B l ) 2 R M S {\displaystyle R_{ES}={\frac {(Bl)^{2}}{R_{MS}}}} R M S {\displaystyle R_{MS}} R A S = R M S S D 2 {\displaystyle R_{AS}={\frac {R_{MS}}{S_{D}^{2}}}}
箱体合规性
L C E B = ( B l ) 2 C A B S D 2 {\displaystyle L_{CEB}={\frac {(Bl)^{2}C_{AB}}{S_{D}^{2}}}} C M B = C A B S D 2 {\displaystyle C_{MB}={\frac {C_{AB}}{S_{D}^{2}}}} C A B {\displaystyle C_{AB}}
箱体漏气损失
R E L = ( B l ) 2 S D 2 R A L {\displaystyle R_{EL}={\frac {(Bl)^{2}}{S_{D}^{2}R_{AL}}}} R M L = S D 2 R A L {\displaystyle R_{ML}=S_{D}^{2}R_{AL}} R A L {\displaystyle R_{AL}}
端口的声学质量
C M E P = S D 2 M A P ( B l ) 2 {\displaystyle C_{MEP}={\frac {S_{D}^{2}M_{AP}}{(Bl)^{2}}}} M M P = S D 2 M A P {\displaystyle M_{MP}=S_{D}^{2}M_{AP}} M A P {\displaystyle M_{AP}}
箱体质量负载
见 C M E C {\displaystyle C_{MEC}}
见 M M C {\displaystyle M_{MC}}
M A B {\displaystyle M_{AB}}
低频辐射质量负载
见 C M E C {\displaystyle C_{MEC}}
见 M M C {\displaystyle M_{MC}}
M A 1 {\displaystyle M_{A1}}
组合质量负载
C M E C = S D 2 M A C ( B l ) 2 {\displaystyle C_{MEC}={\frac {S_{D}^{2}M_{AC}}{(Bl)^{2}}}} = S D 2 ( M A B + M A 1 ) + M M D ( B l ) 2 {\displaystyle ={\frac {S_{D}^{2}(M_{AB}+M_{A1})+M_{MD}}{(Bl)^{2}}}} M M C = S D 2 ( M A B + M A 1 ) + M M D {\displaystyle M_{MC}=S_{D}^{2}(M_{AB}+M_{A1})+M_{MD}} M A C = M A D + M A B + M A 1 {\displaystyle M_{AC}=M_{AD}+M_{AB}+M_{A1}} = M M D S D 2 + M A B + M A 1 {\displaystyle ={\frac {M_{MD}}{S_{D}^{2}}}+M_{AB}+M_{A1}}
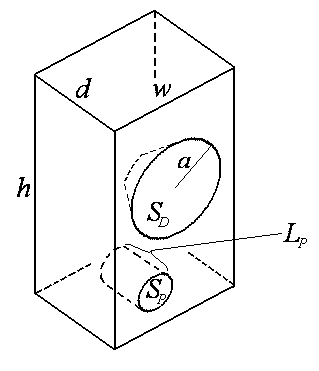
图 7:低音反射外壳的重要尺寸。
基于这些尺寸 [1],
C A B = V A B ρ 0 c 0 2 {\displaystyle C_{AB}={\frac {V_{AB}}{\rho _{0}c_{0}^{2}}}} M A B = B ρ e f f π a {\displaystyle M_{AB}={\frac {B\rho _{eff}}{\pi a}}}
B = d 3 ( S D S B ) 2 π S D + 8 3 π [ 1 − S D S B ] {\displaystyle B={\frac {d}{3}}\left({\frac {S_{D}}{S_{B}}}\right)^{2}{\sqrt {\frac {\pi }{S_{D}}}}+{\frac {8}{3\pi }}\left[1-{\frac {S_{D}}{S_{B}}}\right]} ρ 0 ≤ ρ e f f ≤ ρ 0 ( 1 − V f i l l V B ) + ρ f i l l V f i l l V B {\displaystyle \rho _{0}\leq \rho _{eff}\leq \rho _{0}\left(1-{\frac {V_{fill}}{V_{B}}}\right)+\rho _{fill}{\frac {V_{fill}}{V_{B}}}}
V A B = V B [ 1 − V f i l l V B ] [ 1 + γ − 1 1 + γ ( V B V f i l l − 1 ) ρ 0 c a i r ρ f i l l c f i l l ] {\displaystyle V_{AB}=V_{B}\left[1-{\frac {V_{fill}}{V_{B}}}\right]\left[1+{\frac {\gamma -1}{1+\gamma \left({\frac {V_{B}}{V_{fill}}}-1\right){\frac {\rho _{0}c_{air}}{\rho _{fill}c_{fill}}}}}\right]}
V B = h w d {\displaystyle V_{B}=hwd} S B = w h {\displaystyle S_{B}=wh}
c a i r = {\displaystyle c_{air}=} c f i l l = {\displaystyle c_{fill}=} V f i l l i n g {\displaystyle V_{filling}}
ρ 0 = {\displaystyle \rho _{0}=} m 3 {\displaystyle {\rm {m^{3}}}} ρ f i l l = {\displaystyle \rho _{fill}=}
γ = {\displaystyle \gamma =} c 0 = {\displaystyle c_{0}=}
ρ e f f {\displaystyle \rho _{eff}} ρ e f f ≈ ρ 0 {\displaystyle \rho _{eff}\approx \rho _{0}}
← 密封箱低音扬声器设计 · 聚合物薄膜声学滤波器 →
















![{\displaystyle Z_{RAD}={\frac {\rho _{0}c}{\pi a^{2}}}\left[\left(1-{\frac {J_{1}(2ka)}{ka}}\right)+j{\frac {H_{1}(2ka)}{ka}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5e006665dedc46a37c8d0506bd6284be643f0c8)



































































![{\displaystyle \cos[n\cos ^{-1}(\Omega )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b76c5102b116d999426586f1bf89f8c5a87b46cb)

![{\displaystyle \cosh[n\cosh ^{-1}(\Omega )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce1ff5479bfec74e8ba99ed95755fe02942d1347)







![{\displaystyle 10{\rm {{log}[1+\epsilon ^{2}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f535dd5d71df8c646b4e347a66f617f5d0c691eb)






![{\displaystyle \omega _{0}=\omega _{n}{\sqrt[{8}]{\frac {64\epsilon ^{2}}{1+\epsilon ^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82d036e5d4d3fa7594ad910300c2250c7ae58b56)
![{\displaystyle k=\tanh \left[{\frac {1}{4}}\sinh ^{-1}\left({\frac {1}{\epsilon }}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d50f1f1444578d83c79eeeac312edb80650d8cda)

![{\displaystyle a_{1}={\frac {k{\sqrt {4+2{\sqrt {2}}}}}{\sqrt[{4}]{D}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e53d7b5c7cb6915e35bccc02700ade45fe6e06be)

![{\displaystyle a_{3}={\frac {a_{1}}{\sqrt {D}}}\left[1-{\frac {1-k^{2}}{2{\sqrt {2}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90ce005b7b6658ea9a20b36864abb53ea18b50d9)



























![{\displaystyle B={\frac {d}{3}}\left({\frac {S_{D}}{S_{B}}}\right)^{2}{\sqrt {\frac {\pi }{S_{D}}}}+{\frac {8}{3\pi }}\left[1-{\frac {S_{D}}{S_{B}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72968d621ea65e2da8e0409a3c5ff832b0e55522)

![{\displaystyle V_{AB}=V_{B}\left[1-{\frac {V_{fill}}{V_{B}}}\right]\left[1+{\frac {\gamma -1}{1+\gamma \left({\frac {V_{B}}{V_{fill}}}-1\right){\frac {\rho _{0}c_{air}}{\rho _{fill}c_{fill}}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/160f946f6aa6c8211bf526b5f0a694865bdcadf9)











