算法/动态规划

顶部，章节：1，2，3，4，5，6，7，8，9，A

动态规划 可以被认为是一种针对特定回溯算法的优化技术，这些回溯算法会反复地解决子问题。注意，动态规划中的“动态”一词不应该与动态编程语言混淆，比如 Scheme 或 Lisp。“编程”一词也不应该与编写计算机程序的行为混淆。在算法的语境中，动态规划总是指用从其他表格值计算出的值来填充表格的技术。（它之所以是动态的，是因为表格中的值是根据表格的其他值由算法填充的；它之所以是编程，是指在表格中设置值，就像电视节目安排关注的是何时播放什么节目一样。）

斐波那契数列

在介绍动态规划技术之前，先展示一个相关的技术，称为记忆化，以一个玩具例子来说明：斐波那契数列。我们想要的是一个计算第n个斐波那契数的程序。

// fib -- compute Fibonacci(n)
function fib(integer n): integer

根据定义，第n个斐波那契数，表示为 ${\textrm {F}}_{n}$ 是

{\textrm {F}}_{0}=0

{\textrm {F}}_{1}=1

{\textrm {F}}_{n}={\textrm {F}}_{n-1}+{\textrm {F}}_{n-2}

如何创建一个用于查找第 n 个斐波那契数的好算法？让我们从一个朴素的算法开始，它对数学定义进行编码。

// fib -- compute Fibonacci(n)
function fib(integer n): integer
  assert (n >= 0)
  if n == 0: return 0 fi
  if n == 1: return 1 fi
  
  return fib(n - 1) + fib(n - 2)
end

这个代码示例也在 Ada 中提供。

注意，这是一个玩具例子，因为已经存在一个关于 ${\textrm {F}}_{n}$ 的数学闭式解。

F(n)={\phi ^{n}-(1-\phi )^{n} \over {\sqrt {5}}}

其中

\phi ={1+{\sqrt {5}} \over 2}

此后一个等式被称为黄金分割。因此，一个程序可以有效地计算出 ${\textrm {F}}_{n}$ 即使对于非常大的n。但是，了解当前算法的低效之处是很有启发性的。

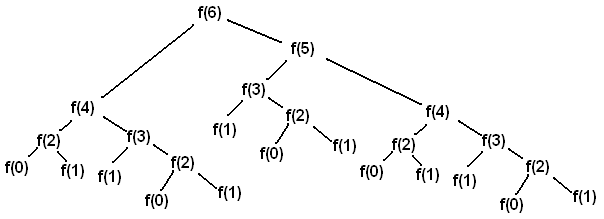
为了分析fib 的运行时间，我们应该看看一个甚至像第 6 个斐波那契数一样小的数字的调用树。

调用树的每个叶子都有值 0 或 1，这些值的总和是最终结果。因此，对于任何n，调用树中的叶子数实际上等于 ${\textrm {F}}_{n}$ 本身！闭式解因此告诉我们 fib(n) 中的叶子数近似等于

\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}\approx 1.618^{n}=2^{\lg(1.618^{n})}=2^{n\lg(1.618)}\approx 2^{0.69n}.

(注意上面使用的代数运算，将指数的底数改为 2。)这意味着叶子数量过多，特别是考虑到上面调用树中重复出现的模式。

我们可以进行的一种优化是，在计算出结果后将其保存到表中，这样同一结果只需计算一次。优化过程称为记忆化，并符合以下方法

记忆化方法

从回溯算法开始
在表中查找问题；如果存在有效条目，则返回该值
否则，递归计算问题，然后在返回该值之前将结果存储在表中

考虑回溯章节中针对最长公共子序列问题的解决方案。在该算法的执行过程中，许多公共子问题被重复计算。作为优化，我们可以计算这些子问题一次，然后存储结果以供以后读取。递归记忆化算法可以“自下而上”地转换为迭代算法，该算法填充子问题的解决方案表。一些解决的子问题在最终结果中可能不需要（这就是动态规划与记忆化的区别），但动态规划非常有效，因为迭代版本可以更好地利用缓存并减少调用开销。渐近地，动态规划和记忆化具有相同的复杂度。

那么，使用记忆化的斐波那契程序如何工作呢？考虑以下程序（f[n] 包含第 n 个斐波那契数，如果已计算，否则为 -1）

function fib(integer n): integer
  if n == 0 or n == 1:
    return n
  else-if f[n] != -1:
    return f[n]
  else
    f[n] = fib(n - 1) + fib(n - 2)
    return f[n]
  fi
end

此代码示例也适用于 Ada。

代码应该非常清楚。如果 fib(n) 的值已经计算出来，它将存储在 f[n] 中，然后返回，而不是再次计算。这意味着所有子调用树的副本都从计算中删除了。

蓝色框中的值是已经计算过的值，因此可以跳过调用。因此，它比直接的递归算法快得多。由于每个小于 n 的值都计算一次，并且只计算一次，因此在第一次执行时，渐近运行时间为 $O(n)$ 。对它的任何其他调用将花费 $O(1)$ ，因为这些值已经预先计算出来了（假设每个后续调用的参数都小于 n）。

该算法确实会消耗大量内存。当我们计算 fib(n) 时，fib(0) 到 fib(n) 的值将存储在主内存中。可以改进吗？是的，可以，尽管后续调用的 $O(1)$ 运行时间显然会丢失，因为这些值不会被存储。由于 fib(n) 的值仅取决于 fib(n-1) 和 fib(n-2)，我们可以通过自下而上地丢弃其他值。如果我们要计算 fib(n)，我们首先计算 fib(2) = fib(0) + fib(1)。然后，我们可以通过添加 fib(1) 和 fib(2) 来计算 fib(3)。之后，可以丢弃 fib(0) 和 fib(1)，因为我们不再需要它们来计算任何其他值。从 fib(2) 和 fib(3) 我们计算 fib(4) 并丢弃 fib(2)，然后我们计算 fib(5) 并丢弃 fib(3)，等等。代码如下

function fib(integer n): integer
  if n == 0 or n == 1:
    return n
  fi

  let u := 0
  let v := 1

  for i := 2 to n:
    let t := u + v
    u := v
    v := t
  repeat
  
  return v
end

此代码示例也适用于 Ada。

我们可以修改代码以将值存储在数组中以供后续调用，但重点是我们不需要这样做。这种方法是动态规划的典型方法。首先，我们确定要解决哪些子问题才能解决整个问题，然后我们使用迭代过程自下而上地计算这些值。

最长公共子序列（DP 版本）

最长公共子序列 (LCS) 问题涉及比较两个给定的字符序列，以找到这两个序列共有的最长子序列。

请注意，“子序列”不是“子串” - 出现在子序列中的字符不必在两个序列中都是连续的；但是，单个字符确实需要以与两个序列中出现的顺序相同的顺序出现。

给定两个序列，即

X = {x₁, x₂, x₃, ..., x_m} 和 Y = {y₁, y₂, y₃, ..., y_n}

我们定义：

Z = {z₁, z₂, z₃, ..., z_k}

作为 X 的子序列，如果所有字符 z₁, z₂, z₃, ..., z_k 出现在 X 中，并且它们以严格递增的顺序出现；即 z₁ 出现在 X 中，先于 z₂，后者又先于 z₃，依此类推。再次强调，所有字符 z₁, z₂, z₃, ..., z_k 不必连续；它们只需要以与 Z 中相同的顺序出现在 X 中。因此，我们可以将 Z = {z₁, z₂, z₃, ..., z_k} 定义为 X 和 Y 的公共子序列，如果 Z 同时出现在 X 和 Y 中作为子序列。

LCS 的回溯解决方案涉及枚举 X 的所有可能的子序列，并检查每个子序列是否也是 Y 的子序列，并跟踪我们找到的最长子序列 [参见 最长公共子序列（穷举版本） ]。由于 X 中有 m 个字符，这会导致 2^m 种可能的组合。因此，这种方法需要指数时间，对于长序列来说是不切实际的。

矩阵链乘法

假设您需要将一系列 $n$ 个矩阵 $M_{1},\ldots ,M_{n}$ 乘在一起以形成一个乘积矩阵 $P$

P=M_{1}\cdot M_{2}\cdots M_{n-1}\cdot M_{n}

这将需要 $n-1$ 次乘法，但我们以最快的方式形成这个乘积的方法是什么？矩阵乘法是结合的，即

(A\cdot B)\cdot C=A\cdot (B\cdot C)

对于任何 $A,B,C$ ，因此我们可以选择先执行哪个乘法运算。(请注意，矩阵乘法不满足交换律，也就是说，通常情况下 $A\cdot B=B\cdot A$ 不成立。)

因为你一次只能乘以两个矩阵，所以乘积 $M_{1}\cdot M_{2}\cdot M_{3}\cdot M_{4}$ 可以用以下方式加括号

((M_{1}M_{2})M_{3})M_{4}

(M_{1}(M_{2}M_{3}))M_{4}

M_{1}((M_{2}M_{3})M_{4})

(M_{1}M_{2})(M_{3}M_{4})

M_{1}(M_{2}(M_{3}M_{4}))

两个矩阵 $M_{1}$ 和 $M_{2}$ 可以相乘，如果 $M_{1}$ 的列数等于 $M_{2}$ 的行数。它们的乘积的行数将等于 $M_{1}$ 的行数，列数将等于 $M_{2}$ 的列数。也就是说，如果 $M_{1}$ 的维度是 $a\times b$ ，而 $M_{2}$ 的维度是 $b\times c$ ，它们的乘积将具有维度 $a\times c$ 。

要将两个矩阵相乘，我们使用一个名为 matrix-multiply 的函数，该函数接受两个矩阵并返回它们的乘积。我们暂时不讨论这个函数的实现，因为它不是本章的重点（如何以最快的方式将两个矩阵相乘已经经过多年的深入研究[TODO: 建议将此主题纳入高级书籍]）。该函数用于乘以大小为 $a\times b$ 和 $b\times c$ 的两个矩阵所需要的时间与标量乘法的次数成正比，而标量乘法的次数又与 $abc$ 成正比。因此，括号的放置方式很重要：假设我们有三个矩阵 $M_{1}$ ， $M_{2}$ 和 $M_{3}$ 。 $M_{1}$ 的维度为 $5\times 100$ ， $M_{2}$ 的维度为 $100\times 100$ ，而 $M_{3}$ 的维度为 $100\times 50$ 。让我们以两种可能的方式对它们进行括号运算，看看哪种方式需要的乘法次数最少。这两种方式分别是

((M_{1}M_{2})M_{3})

，以及

(M_{1}(M_{2}M_{3}))

.

第一种方式的乘积需要 75000 次标量乘法（5*100*100=50000 用于形成乘积 $(M_{1}M_{2})$ ，另需 5*100*50=25000 用于最后的乘法）。这看起来可能很多，但与第二种括号方式所需的 525000 次标量乘法（50*100*100=500000 加上 5*50*100=25000）相比，它就微不足道了！你可以看到为什么确定括号的放置方式很重要：想象一下，如果我们需要乘以 50 个矩阵会发生什么！

形成递归解决方案

请注意，我们专注于找到需要多少次标量乘法，而不是实际的顺序。这是因为一旦我们找到一个有效的算法来找到数量，创建实际括号运算的算法就很简单了。不过，我们会在最后进行讨论。

那么，最佳括号运算算法应该是什么样的呢？从章节标题中，你可能会想到使用动态规划方法（当然不是要给出答案）。那么，动态规划方法应该如何工作呢？由于动态规划算法是基于最优子结构的，那么这个问题中的最优子结构是什么呢？

假设最佳的括号运算方式是

M_{1}M_{2}\dots M_{n}

在 $k$ 处分割乘积

(M_{1}M_{2}\dots M_{k})(M_{k+1}M_{k+2}\dots M_{n})

.

那么，最优解包含两个子问题的最优解

(M_{1}\dots M_{k})

(M_{k+1}\dots M_{n})

也就是说，正如动态规划的基本原理一样，问题的解依赖于更小子问题的解。

假设用 $c(n)$ 个标量乘法来计算矩阵 $M_{n}$ 和 $M_{n+1}$ 的乘积，而 $f(m,n)$ 是对矩阵 $M_{m}\dots M_{n}$ 进行最优括号化所需的标量乘法次数。 $f(m,n)$ 的定义是迈向解决方案的第一步。

当 $n-m=1$ 时，公式很简单，就是 $c(m)$ 。但是当距离更大时呢？使用上面的观察结果，我们可以推导出一个公式。假设问题的最优解将矩阵在矩阵 k 和 k+1 处分割（即 $(M_{m}\dots M_{k})(M_{k+1}\dots M_{n})$ ），那么标量乘法次数为。

f(m,k)+f(k+1,n)+c(k)

也就是说，形成第一个产品的所需时间，形成第二个产品的所需时间，以及将它们相乘所需的时间。但是，这个最佳值k是什么呢？答案当然是使上述公式取最小值的那个值。因此，我们可以形成该函数的完整定义

f(m,n)={\begin{cases}\min _{m\leq k<n}f(m,k)+f(k+1,n)+c(k)&{\mbox{if }}n-m>1\\0&{\mbox{if }}n=m\end{cases}}

对此的直接递归解决方案将类似于以下内容 (语言是 Wikicode)

function f(m, n) {

    if m == n
        return 0

    let minCost :=  $\infty$ 

    for k := m to n - 1 {
        v := f(m, k) + f(k + 1, n) + c(k)
        if v < minCost
            minCost := v
    }
    return minCost
}

不幸的是，这种相当简单的解决方案并不是一个很好的解决方案。它花费大量时间重新计算数据，并且其运行时间呈指数级增长。

要做的
对直接递归方法进行分析

要做的
编写一个记忆版本

使用与上述相同的适应方法，我们得到

function f(m, n) {

    if m == n
        return 0

    else-if f[m,n] != -1:
      return f[m,n]
    fi

    let minCost :=  $\infty$ 

    for k := m to n - 1 {
        v := f(m, k) + f(k + 1, n) + c(k)
        if v < minCost
            minCost := v
    }
    f[m,n]=minCost
    return minCost
}

要做的
编写一个完整的DP版本

解析任何上下文无关文法

请注意，与这种技术相比，特殊类型的上下文无关文法可以更有效地解析，但在通用性方面，DP方法是唯一可行的。

顶部，章节：1，2，3，4，5，6，7，8，9，A