顶部,章节:1,2,3,4,5,6,7,8,9,A
在我们开始学习算法技术之前,我们将先绕道介绍一些必要的数学工具。首先,我们将介绍一些将在本书后面使用的术语的数学定义。通过扩展你的数学词汇,你可以更加精确地描述问题或更容易地表达问题。然后,我们将介绍分析算法运行时间的方法。在本专著中,我们将在介绍每个主要算法之后给出其运行时间的分析以及其正确性的证明。
除了正确性之外,另一个重要的算法特征是其时间和内存消耗。时间和内存都是宝贵的资源,它们在使用方式上存在显著差异(即使两者都充足)。
如何衡量资源消耗?一种方法是创建一个函数,用输入的一些特征来描述资源的使用情况。一个常用的输入数据集特征是其大小。例如,假设一个算法以一个包含  个整数的数组作为输入。我们可以将这个算法所需的时间描述为一个以
个整数的数组作为输入。我们可以将这个算法所需的时间描述为一个以  为变量的函数
为变量的函数  。例如,我们可以写成
。例如,我们可以写成

其中  是某个时间单位(在本讨论中,主要关注的是时间,但我们也可以用它来描述内存消耗)。时间单位很少是实际的秒数,因为这会取决于机器本身、它运行的系统以及系统负载。相反,时间单位通常用执行某些基本操作的次数来表示。例如,我们可能关心的一些基本操作包括:所需的加法或乘法次数;元素比较次数;内存位置交换次数;或执行的机器指令数量。通常,我们可能会简单地将这些执行的基本操作称为执行的步骤。
是某个时间单位(在本讨论中,主要关注的是时间,但我们也可以用它来描述内存消耗)。时间单位很少是实际的秒数,因为这会取决于机器本身、它运行的系统以及系统负载。相反,时间单位通常用执行某些基本操作的次数来表示。例如,我们可能关心的一些基本操作包括:所需的加法或乘法次数;元素比较次数;内存位置交换次数;或执行的机器指令数量。通常,我们可能会简单地将这些执行的基本操作称为执行的步骤。
这是否是确定算法资源消耗的好方法?是也不是。当两种不同的算法在时间消耗上相似时,精确的函数可能有助于确定在给定条件下哪个算法更快。但在许多情况下,计算执行所需操作确切数量的解析描述要么很困难,要么根本不可能,尤其是在算法根据其输入的值有条件地执行操作时。相反,真正重要的是不是完成函数所需的精确时间,而是资源消耗根据其输入变化的程度。具体而言,考虑以下两个函数,它们分别代表每个输入数据集大小所需的计算时间


它们看起来很不同,但它们的行为如何?让我们看看函数的一些图像( 为红色,
为红色, 为蓝色)
为蓝色)
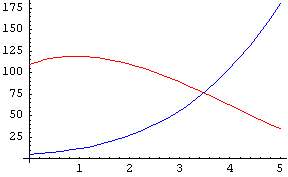 f 和 g 在 0 到 5 范围内的图像 f 和 g 在 0 到 5 范围内的图像 |
 f 和 g 在 0 到 15 范围内的图像 f 和 g 在 0 到 15 范围内的图像
|
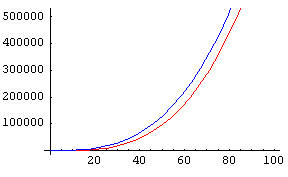 f 和 g 在 0 到 100 范围内的图像 f 和 g 在 0 到 100 范围内的图像 |
 f 和 g 在 0 到 1000 范围内的图像 f 和 g 在 0 到 1000 范围内的图像
|
在第一个非常有限的图像中,曲线看起来有些不同。在第二个图像中,它们开始以某种方式呈现相同的趋势,在第三个图像中,它们之间只有很小的差异,最后它们几乎完全相同。实际上,它们逼近  ,即主导项。当 n 变大时,其他项与 n3 相比变得微不足道。
,即主导项。当 n 变大时,其他项与 n3 相比变得微不足道。
正如你所看到的,修改多项式时间算法的低阶系数并没有太大帮助。真正重要的是最高阶系数。这就是为什么我们采用了这种符号来进行这种分析。我们说

我们忽略了低阶项。我们可以说

这为我们提供了一种更便捷的方式来比较不同的算法。对 个元素进行插入排序需要
个元素进行插入排序需要 数量级的步骤。归并排序的排序步骤为
数量级的步骤。归并排序的排序步骤为 。因此,一旦输入数据集足够大,归并排序就会比插入排序更快。
。因此,一旦输入数据集足够大,归并排序就会比插入排序更快。
一般来说,我们写

当

也就是说, 成立当且仅当存在一些常数
成立当且仅当存在一些常数 和
和 ,使得对于所有
,使得对于所有 ,
, 为正且小于等于
为正且小于等于 。
。
注意,此符号中使用的等号描述了 和
和 之间的关系,而不是反映真正的相等性。鉴于此,有些人用集合来定义大O符号,指出
之间的关系,而不是反映真正的相等性。鉴于此,有些人用集合来定义大O符号,指出

当

大O符号只是一个上界;这两个都是真的


如果我们将等号用作等式,我们会得到非常奇怪的结果,例如

这显然是胡说八道。这就是为什么集合定义很方便。你可以通过将等号视为单向等式来避免这些情况,即

并不意味着

始终将 O 保持在右侧。
有时,我们想要更多地了解某个函数行为的上界。大 Omega 提供了下界。一般来说,我们说

当

即  当且仅当存在常数 c 和 n0 使得对于所有 n>n0 f(n) 为正且大于或等于 cg(n)。
当且仅当存在常数 c 和 n0 使得对于所有 n>n0 f(n) 为正且大于或等于 cg(n)。
所以,例如,我们可以说
 ,(c=1/2, n0=4) 或
,(c=1/2, n0=4) 或 ,(c=1, n0=3),
,(c=1, n0=3),
但声称

当给定函数同时为 O(g(n)) 和 Ω(g(n)) 时,我们说它是 Θ(g(n)),并且我们对该函数有了严格的界限。函数 f(n) 为 Θ(g(n)) 时

但大多数时候,当我们试图证明给定的  时,我们并不使用这个定义,而是证明它同时是 O(g(n)) 和 Ω(g(n))。
时,我们并不使用这个定义,而是证明它同时是 O(g(n)) 和 Ω(g(n))。
当渐近界限不紧密时,我们可以用  或
或  来表达。定义如下:
来表达。定义如下:
- f(n) 是 o(g(n)) 当且仅当
 ,并且
,并且
- f(n) 是 ω(g(n)) 当且仅当

请注意,当对于 g 的任何系数,g 最终都大于 f 时,函数 f 属于 o(g(n));而对于 O(g(n)),只需要存在一个系数,使得 g 最终至少与 f 一样大。
给定两个参数的函数  和
和  ,
,
 当且仅当
当且仅当  。
。
例如, ,以及
,以及  。
。
合并排序 n 个元素: 这描述了合并排序的一次迭代:问题空间
这描述了合并排序的一次迭代:问题空间  被缩减成两个一半 (
被缩减成两个一半 ( ),然后在所有递归调用结束时合并在一起 (
),然后在所有递归调用结束时合并在一起 ( )。这个符号系统是算法分析的精髓,所以要习惯它。
)。这个符号系统是算法分析的精髓,所以要习惯它。
有一些定理可以用来估计一个函数的 Big Oh 时间,前提是它的递归方程符合某种模式。

|
要
写这部分
|
对你的方程的 Big Oh 时间做一个猜测。然后使用归纳法证明这个猜测是正确的。

|
要
写这部分
|

|
要
展示常用求和的封闭形式并证明它们
|
这实际上只是一种获得明智猜测的方法。你仍然必须回到替换法来证明 Big Oh 时间。

|
要
写这部分
|
考虑一个递归方程,它符合以下公式

对于 a ≥ 1, b > 1 和 k ≥ 0。这里,a 是每次函数调用产生的递归调用次数,n 是输入大小,b 是每次输入缩小多少,k 是每次函数调用(除了基本情况)执行的操作的多项式阶数。例如,在后面介绍的合并排序算法中,我们有

因为每次非基本情况迭代都会调用两个子问题,并且数组的大小每次都会减半。最后的  是这个分治算法的“征服”部分:将两个递归调用的结果合并成最终结果需要线性时间。
是这个分治算法的“征服”部分:将两个递归调用的结果合并成最终结果需要线性时间。
将 T 的递归调用视为形成一棵树,有三种可能的情况来确定算法的大部分时间都花在哪里(这里“大部分”指的是它的渐进行为)
- 这棵树可能是头重脚轻的,大部分时间花在接近根部的初始调用上;
- 这棵树可能有一个稳定状态,时间均匀分布;或者
- 这棵树可能头轻脚重,大部分时间花在接近叶子的调用上
根据树处于这三种状态中的哪一种,T 将有不同的复杂度
对于上面提到的归并排序示例,其中

我们有

因此, ,所以这也处于“稳定状态”:根据主定理,归并排序的复杂度因此为
,所以这也处于“稳定状态”:根据主定理,归并排序的复杂度因此为
 .
.
(从图的邻接表表示开始,并显示两个嵌套的for循环:一个用于每个节点n,另一个嵌套在该循环中,用于每个边e。如果有n个节点和m个边,这可能导致你说循环需要O(nm)时间。但是,只有在一次循环中,内部循环才能花费那么长时间,更紧密的界限是O(n+m)。)
顶部,章节:1,2,3,4,5,6,7,8,9,A




























































