算法/爬山法

顶部，章节：1，2，3，4，5，6，7，8，9，A

爬山法是一种用于特定优化问题的技术。其思想是从问题的次优解开始（即，从山脚开始），然后重复改进解（爬山），直到某个条件最大化（到达山顶）。

爬山法方法

构建满足问题约束的次优解
取该解并对其进行改进
重复改进解，直到不再需要/能够进行改进

最流行的爬山问题之一是网络流问题。尽管网络流听起来可能有些具体，但它很重要，因为它具有很高的表达能力：例如，实际应用中遇到的许多算法问题实际上可以被视为网络流的特例。在介绍了爬山方法用于数值问题的简单示例之后，我们将介绍网络流，然后介绍网络流应用示例。

牛顿求根法

牛顿求根法是一种已有三个世纪的算法，用于寻找函数根的数值近似值（即，函数f(x) 变为零的点 $x$ ），从初始猜测开始。您需要知道此算法的函数 $f(x)\,$ 及其一阶导数 $f'(x)\,$ 。其思想如下：在初始猜测 $x_{0}$ 的附近，我们可以形成函数的泰勒展开式

f(x)=f(x_{0}+\epsilon )\,

\approx f(x_{0})+\epsilon f'(x_{0})

+{\frac {\epsilon ^{2}}{2}}f''(x_{0})+...

这给出了在 $x_{0}$ 附近对函数的良好逼近。只取右手边的前两项，将它们设为零，并解出 $\epsilon$ ，我们得到

\epsilon =-{\frac {f(x_{0})}{f'(x_{0})}}

我们可以用它来构建更好的解决方案

x_{1}=x_{0}+\epsilon =x_{0}-{\frac {f(x_{0})}{f'(x_{0})}}.

这个新的解可以作为再次应用相同过程的起点。因此，一般来说，可以通过反复应用以下公式来构建更好的近似值

x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}.

如插图所示，这不过是根据初始猜测点的切线构建零点。一般来说，牛顿求根法是二次收敛的，除非解的一阶导数 $f'(x)=0\,$ 在根处消失。

回到“爬山”的类比，我们可以将牛顿求根法应用于函数 $f(x)\,$ ，而应用于它的导数 $f'(x)\,$ ，也就是说寻找 $x$ ，使得 $f'(x)=0\,$ 。这将给出函数的极值位置，即它的最大值和最小值。以这种方式从足够接近最大值的点开始牛顿法，我们就爬上了山。

牛顿法的示例应用

净现值函数是时间、利率和一系列现金流的函数。一个相关的函数是内部收益率。每期的公式为 (CF_i x (1+ i/100) ^t，这将得到一个多项式函数，即总现金流，当利率等于 IRR 时等于零。在使用牛顿法时，x 是利率，y 是总现金流，该方法将使用多项式的导数函数来找到给定利率（x 值）下图形的斜率，这将给出 x_n+1，或在下一轮迭代中尝试找到总回报为零的目标 x 的更好的利率。

除了连续函数，爬山法也可以应用于离散网络。

网络流

假设你有一个有向图（可能包含循环），其中一个顶点标记为源点，另一个顶点标记为目的地或“汇点”。源点只有从它发出的边，没有进入它的边。类似地，目标点只有进入它的边，没有从它发出的边。我们可以假设图是完全连通的，没有死胡同；也就是说，对于每个顶点（除了源点和汇点），至少有一条边进入该顶点，还有一条边从该顶点发出。

我们将一个“容量”分配给每条边，最初我们将只考虑整数值容量。以下图形满足我们的要求，其中“s”是源点，“t”是目的地

现在，我们想想象有一系列输入到达源点，我们希望通过边将其运送到汇点。我们一次可以发送到边上的单位数必须小于或等于边的容量。你可以将顶点视为城市，将边视为城市之间的道路，我们希望从源城市尽可能多地将汽车发送到目的地城市。约束条件是，我们不能沿着一条道路发送超过其容量的汽车。

网络流的目标是尽可能多地将流量从 $s$ 发送到 $t$ ，因为每条街道都能承受。

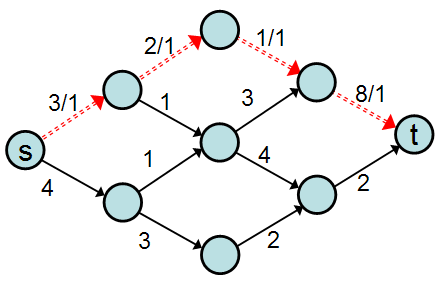
为了组织交通路线，我们可以建立一个从城市 $s$ 到城市 $t$ 的不同路径的列表。每条路径的承载能力等于路径上任意一条边的最小容量值；例如，考虑以下路径 $p$

即使 $p$ 的最后一条边的容量为 8，但该边上只有一辆车行驶，因为它前面的边的容量只有 1（因此，该边已满负荷）。使用这条路径后，我们可以通过从每条边的容量中减去 1 来计算残差图

(我们从每个边在 $p$ 中的容量中减去了 1，因为 1 是 $p$ 的承载能力。）我们可以说路径 $p$ 的流量为 1。正式来说，流量是将值分配给图中边集合的赋值 $f(e)$ ，其中图 $G=(V,E)$ 中的边集合。

1.

\forall e\in E:f(e)\in \mathbb {R}

2.

\forall (u,v)\in E:f((u,v))=-f((v,u))

3.

\forall u\in V,u\neq s,t:\sum _{v\in V}f(u,v)=0

4.

\forall e\in E:f(e)\leq c(e)

其中 $s$ 是源节点， $t$ 是汇节点， $c(e)\geq 0$ 是边 $e$ 的容量。我们将流量 $f$ 的值定义为

{\textrm {Value}}(f)=\sum _{v\in V}f((s,v))

网络流的目标是找到一个 $f$ ，使得 ${\textrm {Value}}(f)$ 最大。最大意味着没有其他满足约束 1-4 的流量赋值，其值会更高。流量约束可以解释为交通中的含义

$\forall e\in E:f(e)\in \mathbb {R}$ 。这条规则简单地定义了流量为从图中边到实数的函数。该函数在图中所有边上都定义了。你也可以将“函数”视为映射：每条边可以是数组的索引，数组中边的值就是该边上流量函数的值。
$\forall (u,v)\in E:f((u,v))=-f((v,u))$ 。这条规则表明，如果从节点 *u* 到节点 *v* 有流量，那么从 *v* 到 *u* 的流量应视为负值。例如，如果有两辆车从城市 *u* 流向城市 *v*，那么负两辆车就会往另一个方向行驶。同样地，如果有三辆车从城市 *u* 流向城市 *v*，而有两辆车从城市 *v* 流向城市 *u*，那么净效应与一辆车从城市 *u* 流向城市 *v*，而没有车从城市 *v* 流向城市 *u* 相同。
$\forall u\in V,u\neq s,t:\sum _{v\in V}f(u,v)=0$ 。这条规则表明，净流量（除源点和汇点之外）应该是中性的。也就是说，你不会有更多汽车进入一个城市，比你离开那个城市的汽车多。新车只能从源点进来，而汽车只能存储在汇点。同样地，从 *s* 流出的任何流量最终都必须流入 *t*。请注意，如果一个城市有三辆车驶入，它可以将两辆车送到一个城市，而剩余的一辆车送到另一个城市。此外，一个城市可能会有来自多个来源的车驶入（尽管所有这些最终都来自城市 *s*）。
$\forall e\in E:f(e)\leq c(e)$ .

Ford-Fulkerson 算法

以下算法计算给定图（具有非负容量）的最大流。算法执行的操作很容易理解，但要证明它会终止并提供最优解并不容易。

function net-flow(graph (V, E), node s, node t, cost c): flow
  initialize f(e) := 0 for all e in E
  loop while not done
    for all e in E:                         // compute residual capacities
      let cf(e) := c(e) - f(e)
    repeat
    
    let Gf := (V, {e : e in E and cf(e) > 0})

    find a path p from s to t in Gf         // e.g., use depth first search
    if no path p exists: signal done

    let path-capacities := map(p, cf)       // a path is a set of edges
    let m := min-val-of(path-capacities)    // smallest residual capacity of p
    for all (u, v) in p:                    // maintain flow constraints
      f((u, v)) := f((u, v)) + m
      f((v, u)) := f((v, u)) - m
    repeat
  repeat
end

待办事项
解释算法的作用，最好使用图片。解释其运行时间。证明它是最优的。展示一个优化方案，通过“记住”深度优先搜索来减少算法的运行时间。

Ford-Fulkerson 算法使用对广度优先搜索的重复调用（使用队列来安排节点的子节点，使其成为当前节点）。广度优先搜索将每条路径的长度加 1，以便第一条到达目的地的路径（最短路径）将第一个出队。这与使用堆栈形成深度优先搜索形成对比，深度优先搜索将找到通往目标的 *任何* 路径，并检查当前节点的“后代”，但不一定是最短路径。

在一次搜索中，将找到从源点到汇点的路径。在每次新的搜索开始时，所有节点都被标记为未标记。已访问的节点被“标记”，如果再次遇到则不再搜索。最终，所有可达的节点都将在队列中排队，并且无法再从队列的最后一个节点到达任何未标记的节点。
在搜索过程中，排队的节点将记录其发现的“边”（由当前节点、发现的节点、当前流量以及从第一个节点到第二个节点方向的总容量组成）。
这使得能够在到达目标节点后，找到从目标节点到起始节点的逆路径。一旦找到路径，就会检查这些边以找到剩余容量最小的边，这将成为沿着这条路径产生的流量，并且这个数量将从沿着路径的每条边的剩余容量中移除。在剩余容量最小的“瓶颈”边处，将无法再以正向方向进行流量，但仍然可以在反向方向进行流量。
这个过程（对通往目标节点的路径进行广度优先搜索，填充到瓶颈边的剩余容量），将不断重复，直到广度优先搜索无法找到通往目标节点的路径（该节点无法到达，因为通往目标节点的所有边序列的瓶颈边都已填满）。因此，先前找到的路径的副作用的记忆将记录在边的流量中，并影响未来搜索的结果。
最大流的一个重要特性是，流量可以发生在边的反方向，并且反方向的剩余容量等于正方向的当前流量。通常，边正方向的剩余容量等于初始容量减去正向流量。直观地说，这使得有更多选择来最大化流量，因为早期增广路径会阻塞较短路径。
在终止时，算法将保留最后一次广度优先搜索（从起始节点开始，不标记目标节点）结果的标记和未标记状态。
最小割状态是由最后一次不成功的广度优先搜索（从起始节点开始，不标记目标节点）形成的两个标记和未标记节点集。起始节点属于割的一侧，而目标节点属于另一侧。任意地，“在割中”意味着在起始节点一侧，或者是一个标记节点。请回忆一下，给定一条带有流量和剩余容量的边，节点是如何被标记的。

Ford-Fulkerson 最大流/最小割的示例应用

Ford-Fulkerson 的一个应用示例是棒球赛季淘汰赛。问题是球队是否可以通过超过其他球队的总胜场数的某种组合来赢得整个赛季。

这个想法是建立一个流图，其中球队不能超过目标球队在整个赛季中可能获得的最大总胜场数。有一些比赛节点，其边代表两支球队之间剩余的比赛次数，每个比赛节点通过不会限制正向流量的边流出到两个球队节点；球队节点从他们参与的所有比赛接收边。然后，具有胜场限制容量的流出边流向虚拟目标节点。在目标节点的总胜场数将超过其他球队胜场数的某种组合的最大流状态下，倒数第二次深度优先搜索将切断起始节点与图的其余部分，因为由于倒数第二次深度优先搜索（回忆算法第二部分找到路径后对流量的影响），无法流向任何比赛节点。这是因为，在寻求每条路径的最大流时，比赛边的容量将被路径上更远的胜场限制边最大程度地消耗，而任何剩余的比赛容量意味着还有更多的比赛要进行，这将使至少一支球队超过目标球队的最大胜场数。如果一个球队节点在最小割中，那么就有一条通往该球队的边具有剩余容量，这意味着根据前面的陈述，该球队是什么？在最小割中找到的球队集代表什么（提示：考虑比赛节点边）？

二分匹配（实习生匹配）最大值示例

这个匹配问题不包括偏好权重。一组公司提供工作，这些工作被归为一个大集合，而实习生则申请特定公司的特定工作。申请是权重为 1 的边。为了将二分匹配问题转换为最大流问题，将创建虚拟顶点 s 和 t，它们从 s 到所有实习生，以及从所有工作到 t 具有权重为 1 的边。然后使用 Ford-Fulkerson 算法通过增广找到的路径来依次饱和图中的 1 容量边。可能会出现这样的中间状态：剩余的实习生和工作都没有匹配，但是沿着具有剩余容量 = 正向流量 = 1 的反向边回溯（沿着后来广度优先搜索期间出现的更长路径）将否定先前次优的增广路径，并提供进一步的搜索选择以进行匹配，并且仅在达到最大流或最大匹配时终止。

顶端,

章节：1，2，3，4，5，6，7，8，9，A