Cg 编程/Unity/天光漫反射

一个球形建筑物，从上方被阴天照亮，从下方被绿色的水池照亮。注意建筑物照明不同的颜色。

本教程介绍半球照明。

它基于 “漫反射”部分中描述的漫反射逐顶点照明。如果您还没有阅读本教程，建议先阅读。

半球照明基本上是用一个巨大的光源来计算漫反射照明，这个光源覆盖了场景周围的整个半球，例如天空。它通常还包括使用不同颜色从下方照亮另一个半球，因为计算几乎是免费的。在左侧的照片中，球形建筑物被阴天照亮。然而，它周围的绿色水池也照亮了建筑物，导致建筑物下半部分出现明显的绿色照明。

半球照明

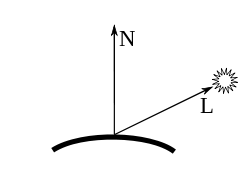
如果我们假设表面上一点周围的半球上的每个点（方向为L）都充当光源，那么我们应该通过积分从半球上所有点积分漫反射照明（由 max(0, L·N) 给出，如 “漫反射”部分所述）。让我们将半球旋转轴的归一化方向称为U（表示“向上”）。如果表面法线N指向U的方向，那么我们具有完全照明，颜色由用户指定。如果它们之间有一个角度 γ（即 cos(γ) = U·N），那么只有半球的一个球形楔形 (参见维基百科文章) 照亮了表面点。与完全照明相比，这种照明的比例 w 为

$w={\frac {1}{2}}(1+\cos(\gamma ))$ $={\frac {1}{2}}(1+\mathbf {U} \cdot \mathbf {N} )$

因此，我们可以将入射光计算为 w 乘以用户指定的半球完全照明的颜色。相反方向的半球将用 1-w 乘以另一种颜色来照亮表面点（如果不需要，它可能是黑色）。下一节解释如何推导出 w 的这个公式。

方程推导

对于任何感兴趣的人（以及因为我在网上找不到它），这里有一个关于 w 方程推导。我们在与表面点相连的球坐标系中对距离 1 处的半球上的照明进行积分，其中N的方向指向y轴的方向。如果N和U指向相同的方向，那么积分（除了用户指定的常数颜色外）为

$\int _{0}^{\pi }\mathrm {d} \phi \int _{0}^{\pi }\mathrm {d} \theta \sin(\theta )\,\mathbf {L} \cdot \mathbf {N} =$ $\int _{0}^{\pi }\mathrm {d} \phi \int _{0}^{\pi }\mathrm {d} \theta \sin(\theta )\left({\begin{array}{c}x\\y\\z\end{array}}\right)\cdot \mathbf {N}$

sin(θ) 项是半径为 1 的球体表面上积分的雅可比行列式，(x, y, z) 为 (cos(φ)sin(θ), sin(φ)sin(θ), cos(θ))，而N = (0,1,0)。因此，积分变为

$\int _{0}^{\pi }\mathrm {d} \phi \int _{0}^{\pi }\mathrm {d} \theta (\sin(\theta ))^{2}\sin(\phi )=\pi$

常数 π 将包含在用户定义的最大照明的颜色中。如果N和U之间有一个角度 γ，其中 cos(γ) = U·N，那么积分仅在球形楔形上（从 γ 到 π）

$w={\frac {1}{\pi }}\int _{\gamma }^{\pi }\mathrm {d} \phi \int _{0}^{\pi }\mathrm {d} \theta (\sin(\theta ))^{2}\sin(\phi )$ $={\frac {1}{2}}(1+\cos(\gamma ))$ $={\frac {1}{2}}(1+\mathbf {U} \cdot \mathbf {N} )$

着色器代码

该实现基于来自“漫反射”部分的代码。在更详细的实现中，将包含其他光源的贡献，例如使用Phong反射模型，如“镜面高光”部分中所述。在这种情况下，半球照明将与环境光以相同的方式包含在内。

但是，这里唯一的照明是由于半球照明。w的方程是

$w={\frac {1}{2}}(1+\mathbf {U} \cdot \mathbf {N} )$

我们在世界空间中实现它，也就是说，我们必须将表面法线向量N转换到世界空间（参见“世界空间中的着色”），而U由用户在世界空间中指定。我们对向量进行归一化并计算w，然后使用w和1-w根据用户指定的颜色计算照明。实际上，这是非常简单的。

Shader "Cg per-vertex hemisphere lighting" {
   Properties {
      _Color ("Diffuse Material Color", Color) = (1,1,1,1) 
      _UpperHemisphereColor ("Upper Hemisphere Color", Color) 
         = (1,1,1,1) 
      _LowerHemisphereColor ("Lower Hemisphere Color", Color) 
         = (1,1,1,1) 
      _UpVector ("Up Vector", Vector) = (0,1,0,0) 
   }
   SubShader {
      Pass {      
         CGPROGRAM
 
         #pragma vertex vert  
         #pragma fragment frag 
 
         #include "UnityCG.cginc"
 
         // shader properties specified by users
         uniform float4 _Color; 
         uniform float4 _UpperHemisphereColor;
         uniform float4 _LowerHemisphereColor;
         uniform float4 _UpVector;
 
         struct vertexInput {
            float4 vertex : POSITION;
            float3 normal : NORMAL;
         };
         struct vertexOutput {
            float4 pos : SV_POSITION;
            float4 col : COLOR;
               // the hemisphere lighting computed in the vertex shader
         };
 
         vertexOutput vert(vertexInput input) 
         {
            vertexOutput output;
 
            float4x4 modelMatrix = unity_ObjectToWorld;
            float4x4 modelMatrixInverse = unity_WorldToObject; 
 
            float3 normalDirection = normalize(
               mul(float4(input.normal, 0.0), modelMatrixInverse).xyz);
            float3 upDirection = normalize(_UpVector);
 
            float w = 0.5 * (1.0 + dot(upDirection, normalDirection));
            output.col = (w * _UpperHemisphereColor 
               + (1.0 - w) * _LowerHemisphereColor) * _Color;
 
            output.pos = mul(UNITY_MATRIX_MVP, input.vertex);
            return output;
         }
 
         float4 frag(vertexOutput input) : COLOR
         {
            return input.col;
         }
 
         ENDCG
      }
   } 
}

总结

恭喜你完成了另一个教程！我们已经看到了

什么是半球照明。
半球照明的方程是什么。
如何实现半球照明。

进一步阅读

如果你还想了解更多

关于漫反射照明，你应该阅读“漫反射”部分。
关于半球照明，你可以阅读Randi Rost等人在2009年由Addison-Wesley出版的书籍“OpenGL 着色语言”（第3版）的第12.1节。

< Cg编程/Unity

除非另有说明，否则本页上的所有示例源代码均授予公有领域。