电路创意/小组 66b

<<< 内容 - 小组 64a - 小组 65a - 小组 66a - 小组 67a - 小组 68a - 页面阶段 >>>

<<< 小组 64b - 小组 65b - 小组 67b - 小组 68b >>>

66b 小组学生页面

我们是来自计算机系统学院，索菲亚技术大学的学生。我们 66 小组分为两个小组；我们构成第二个 - 66b - 小组。以下是我们的姓名

Borislav Bozhanov；Aydin Hafizoglu；Nicklay Lyubenov；Miroslav Otsedarski；Georgi Upalov；Zapyan Dimitrov；Borislav Borisov；Vanya Shiderova；Lyudmila Nenkova；Ana Ivanova；Yanita Petkova；Rumi Pasaoglu；Konstantina Gocheva；Petar Velichkov；Erol Ozturk；Lyubomir Todorov。

实验室 1：研究无源电阻器件

在本节中，我们将解释并展示我们在实验室 1 期间的一些工作。

下图展示了我们在实验室练习中使用的电路图。它包含以下元素

- DAC1,DAC2 (DAC3,DAC4) : 数模转换器；

- ADC1,AC2(ADC3,ADC4) : 模数转换器；

- V1,V2,V3 : 三个电压表；

- R = 4,7KΩ : 一个电位器

- 一台电脑，我们可以在上面观察图表

我们使用两个输入电压（Vin1 和 Vin2）

1. 电势图的图形表示。

2. 移动电位器的滑动触点（Vin1 = 常量，Vin2 = 0）。

在这种情况下，我们进行的是“移动-电压”转换。这意味着，当我们移动滑动触点时，我们改变了输出电压。

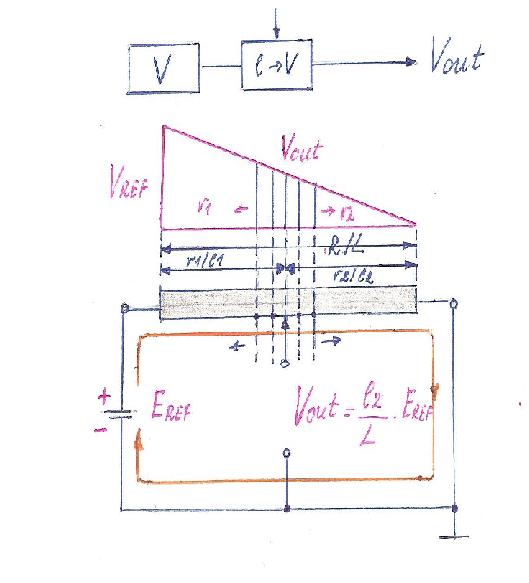
3. 改变 Vin1（电位器阻值不变，Vin2 = 常量）。

在这种情况下，我们进行了“电压-电压”转换。当我们改变电压 Vin1 时，我们改变了 Vout。换句话说，这是一个由左侧控制的“电压-电压”转换器。

4. 改变 Vin1 和 Vin2。

在这种情况下，我们“发明”了电压求和器。

如果这些电压的极性相反，我们的电路将成为一个比较器。在电位器上的某个位置，我们有一个电位为零的点，称为“虚拟地”。

在这里，我们插入了一些关于虚拟地点的维基百科考量。

虚拟地（或虚拟地）是电路中保持在稳定参考电位的节点，而没有直接连接到参考电位。在某些情况下，参考电位被认为是地球表面，因此参考节点被称为“地”或“地球”。

虚拟地概念有助于运算放大器和其他电路中的电路分析，并提供有用的实际电路效果，这些效果用其他方法很难实现。

在电路理论中，一个节点可以具有任何电流或电压值，但虚拟地的物理实现将具有电流处理能力的限制和非零阻抗，这可能会产生实际的副作用。

--Ludmila&Konstantin (讨论) 12:15, 2008 年 5 月 17 日 (UTC)

实验室 2: 改进真正的欧姆实验

2008 年 3 月 18 日星期二，13.45 时

欧姆定律

1. 欧姆定律处理理想导体中电压和电流之间的关系。这种关系表明，理想导体两端的电位差（电压）与其通过的电流成正比。比例常数称为“电阻”，用 R 表示。欧姆定律表示为：V = I.R，其中 V 是两点之间的电位差，包括电阻 R。I 是流过电阻的电流。对于生物学工作，通常更喜欢使用电导率 g = 1/R；在这种形式下，欧姆定律为：I = g.V 2. 服从欧姆定律的材料称为“欧姆材料”或“线性材料”，因为其两端的电位差与其通过的电流呈线性关系。

3. 欧姆定律可用于求解简单电路。完整的电路是指闭合回路。它包含至少一个电压源（从而提供电势能的增加），以及至少一个电位降，即电势能减少的地方。完整电路中各电压的代数和为零。

4. 电路中电势能的增加导致电荷从低电位（即电压）移动到高电位。注意电势能和电位的区别。由于静电力试图将正电荷从高电位移动到低电位，因此电池内部必须有另一个“力”来将电荷从低电位移动到高电位。这种被称为“力”的力称为电动势或emf。emf 的 SI 单位是伏特（因此，它不是真正的力，尽管其名称如此）。我们将使用脚本 E 来表示 emf。

电势能的减少可以通过多种方式发生。例如，由于电路中的电阻导致的热量损失可能是能量下降的一个来源。由于能量守恒，emf 两端的电位差必须等于电路其余部分两端的电位差。也就是说，欧姆定律将得到满足：ε = I.R。

5. 这里有一个很棒的欧姆定律模拟实验，供您测试您对该概念的理解。使用“后退”按钮返回到此位置。 VanyaShiderova66b (讨论)

实验室 3：晶体管电路（试图创建一个“二极管”电流镜像）

2008 年 4 月 8 日星期二，13.45 时 （摘自固态录音机记录的实验室记录） Circuit-fantasist 18:56, 2008 年 5 月 29 日 (UTC)

本实验的目标是将最简单的晶体管电流源（你来自 65b 组的同事一小时前制作的）转换成一个电流镜电路。你可以查看白板上的讨论内容，以及他们制作的原型电路板。首先，我们来分析和讨论他们的作品，然后尝试将其转化成我们想要的电路。

观察白板上你同事留下的电路。你看到了什么？它是什么？这个电路的设计理念是什么？晶体管在那里起什么作用？它的行为是什么样的？电位器在做什么？这些固定的电阻是什么？为什么他们将它们与可变电阻串联？每个元件在这个电路中起什么作用？

让我们开始推理，揭开这个典型晶体管电路的秘密...

理解晶体管

我们必须从某个地方开始；我们需要一些想法来开始讨论... 因此，让我们首先考虑无处不在的晶体管。它是一个三端器件... 他们是如何在这里连接它的？我们如何连接三端元件？他们将其中一个引脚连接到地；因此，三引脚晶体管被连接成一个四引脚器件。此外，为了理解更复杂的三个端晶体管，我们可以将其分解成更简单的两个端部分。例如，我们可以先将输出集电极-发射极部分作为一个两端“元件”，将输入基极-发射极部分作为另一个两端“元件”；然后，开始推理晶体管的作用。

改变输入电流

驱动晶体管最简单的方法是用电流。为此，我们只需要在电源和晶体管的基极之间连接一个基极电阻 Rb；为了简单起见，让我们连接相同的负载电阻 R_L = Rb。结果，我们得到了一个电流放大器（Ic = βIb）而不是我们想要的电流镜（Ic = Ib）。我们如何使电流相等？

改变输入电压

我们可以将第二个电阻（实际上是一个电位器）并联连接到基极-发射极结点，将多余的电流从基极引流到地。我们可以在哪里驱动晶体管？输入是什么？基极和发射极之间的电压驱动晶体管。我们可以在电路的左侧识别出无处不在的电位器和一个串联连接的固定电阻。因此，显然，设计理念是用电压驱动晶体管。晶体管的工作模式是什么（饱和、放大或截止）？还连接了测量设备——两个电压表和一个（毫安）电流表。

我们可以用这个电路做什么？我们可以一个接一个地改变它的属性，并观察它对我们干预的反应。让我们开始改变输入电压。如果我们将 P 的滑块向下移动到末端位置，会发生什么？然后输入电压是多少？零。是的，没有输入电压。晶体管的输出集电极-发射极部分处于截止状态。集电极和发射极之间的电阻无穷大；输出电路中没有电流流动。因此，你可以将晶体管看作一个可变电阻，在这些条件下（零输入电压）它具有无穷大的电阻。为什么电压表 V₁ 显示最大电压（等于电源电压）？解释起来并不容易... 好吧，我们已经讨论过这种现象。我们有一个电阻，它的上端连接到电源的正轨。它的下端电位（相对于地面的电压）是多少？

一种可能的观点是将这个电路看作一个分压器，其中 R₁ = R_L，R₂ = ∞（R₂ >> R₁；因此，K ≈ 1。另一个观点是看到电阻 R₁ 并不起作用，因为没有东西可供它抵抗（没有电流流动）。实际上，电路中没有连接晶体管；我们可以从白板上擦除它...

晶体管只是一个可变电阻

现在开始向上移动电位器的滑块。在给定的时刻，输出电压 V₂ 开始降低；停止时，它位于电源轨（0 - 10 V）之间，例如在中间（5 V）。晶体管的模式是什么（饱和、放大或截止）？它处于“半开”状态；因此，它处于放大模式。晶体管是如何做到这一点的？它做了什么特别的事情吗？不，晶体管在这个区域没有做任何超自然的事情，它所做的事情与真空管、场效应管、变阻器等在它所在的位置所做的事情相同——它只是改变了它当前的电阻。因此，晶体管是一个可变电阻；只是它是一个电控电阻。好吧，如果我们设置了总负载电阻 R_L = 10 kΩ，V_CE = 5 V，晶体管做了什么？它也设置了它当前的电阻 R_CE = 10 kΩ。它只是与集电极电阻相同的电阻。将这个电路看作一个分压器，它有两个相同的电阻；它的传输比为 K = 0.5。

这是关于晶体管的概念，我们需要了解晶体管电路是如何工作的。所有有源元件的作用都是一样的；它们都是电控电阻。因此，所有晶体管电路都包含普通电阻和电控电阻（有源元件）。它们形成了众所周知的分压器，其中晶体管被放置在 R₁、R₂ 或两者位置上。

如果你继续向上移动滑块，你可能会达到饱和状态，其中 V₂ ∞ 0 V，晶体管完全打开。现在的电流是多少？根据欧姆定律，它具有最大值：I = V_CC/R_L。

改变负载电阻

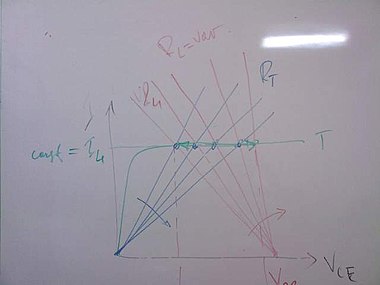
我们是如何得出结论，晶体管的输出部分表现为恒流源的？我们必须以某种方式检查这种推测。为此，我们必须激发电路，看看它将如何对我们的干预做出反应。好吧，如果我们改变负载电阻 R_L，我们会看到什么？输出晶体管特性可以给我们答案。你还记得半导体器件的主题吗？这些特性是他们最喜欢的主题。只是他们没有展示如何使用这种晶体管行为。一位学生：特性是水平的；因此，如果负载变化，电流不会改变。是的，这是正确的。但是晶体管做了什么，它是什么行为导致了这种特性？

如果我们改变负载电阻，电流会改变吗？一位学生：是的，会... 但是你怎么解释呢？因为答案正好相反——电流没有变化... 显然，有些事情与我们的直觉相矛盾，而这就是其中之一... 好吧，看看右边的那张图片（来自 68b 组）；它以图形方式展示了晶体管是如何做到这一点的。两个 IV 特性叠加在同一个坐标系上。第一条曲线是具有电压 V_CC 和内部电阻 R_L 的实际电压源的 IV 特性（他们将其命名为“负载线”）。这条曲线的斜率取决于 R_L。如果 R_L = 0，它是一条垂直线；如果 R_L > 0，它会与电阻成比例地倾斜。第二条曲线代表当前的输出晶体管电阻 (R_CE 或简称为 R_T)。

晶体管做的是以下的技巧：如果我们试图降低/增加负载电阻（以使负载线直立），它会做相反的事情——增加/降低它当前的电阻 (R_CE 或简称为 R_T)，以便交叉（工作）点沿着晶体管几乎水平的输出特性移动。结果，电流几乎保持恒定。你可以看到这个动态恒流源的设计理念是多么简单。它仅包含两个元件：一个电压源和一个与电阻负载串联的动态电阻。动态电阻的电阻补充了负载电阻以达到恒定值 (R_L + R_T = const)；因此，电流是恒定的——I = V_CC/(R_L + R_T)。简而言之，动态电阻保持着电阻的总和恒定。

结论：如果你将晶体管和电阻串联连接起来，并开始改变电阻的电阻，晶体管也将开始改变它当前的电阻，以使电阻的总和保持恒定；结果，电流保持恒定。晶体管充当一个可变的动态电阻，作为电流稳定电阻（具有保持恒定电流特性的元件）。

电阻上的压降呢？它会变化吗？移动滑块并观察 V₂。如果我们降低 R_L，负载上的压降 V_L 也会降低。但是晶体管会增加它当前的电阻 R_T，它上的压降 V₂ 也会增加。反之亦然；如果我们增加 R_L，负载上的压降 V_L 也会增加。现在，晶体管会降低它当前的电阻 R_T，它上的压降 V₂ 也会降低。

结论：如果我们改变负载电阻，电流保持恒定，但电压在很宽的范围内变化。

然而，在某一刻，晶体管耗尽了其储备电阻；它饱和，其两端的电压 V₂ 变为零。动态化的魔力消失，如果继续改变负载电阻，电流将根据欧姆定律变化。

改变电源电压

除了负载电阻，我们还可以改变电源电压。再次看看白板上的图片，回答这个问题，“如果我们改变电源电压 V_CC，电流会保持恒定吗？” 好吧，在实验室设置中试试。正如我们所见，电流发生了变化。为什么？问题是什么？

当我们改变电源电压时，晶体管会像以前一样对这种新的“干预”做出反应：如果我们增加 V_CC，它会增加其目前的电阻 R_T，反之亦然。晶体管将保持一个恒定的比率 V_CC/(R_T + R_L)。但是电流仍然在变化... 原因是什么？一名学生：输入电压变化。是的，这就是原因... 这个电路的悲剧在于，他们用相同的电源为输入电压分压器供电。但我们没有另一个电源。那么我们该怎么做才能使电流在改变公共电源电压时保持恒定呢？

一名学生：...添加另一个晶体管...我不知道；告诉我你将把这个额外的晶体管放在哪里。你必须有一些想法来放置它。晶体管稳定什么？所有同事都理解晶体管稳定电流吗？晶体管是电流稳定器，而二极管是电压稳定器。这种电压稳定元件的特性是垂直线。所有电压稳定元件（二极管、齐纳二极管、LED 等）都具有这样的特性；它们表现得像电压源。

一个真正的二极管设定输入电流

另一名学生：...放置一个二极管...是的，这是正确的答案，放置一个二极管，但现在你必须说在哪里。请在白板上写下来；这里有白板笔。不要因为我们“发明”了在白板上涂鸦的电路而感到困惑。另一个选择是在幻灯片或Powerpoint演示中展示“现成的”漂亮的电路...

好吧，你的同事开始画一个二极管；她是在正确的方向上画的吗？顺便说一句，我知道有些二极管通常是反向连接的。它们是什么？学生：...齐纳二极管...正确，但让我们使用一个普通的二极管。只有，让我们正确地连接它...电路写正确了吗？

另一名学生：让我们擦掉电位器...去画出你的意思。也许，最好不要移除电位器；相反，把它画得更高，并正确连接，作为一个变阻器（不要忘记连接滑块）。把它作为一个让我们能够调节输入电流的元件。现在是拍摄一些照片的时候了。这个房间不太适合拍摄照片，因为它不像好莱坞工作室，但你的同事们做了一些很棒的事情；所以，他们应该被永久保存下来：）

你不觉得是时候在网络上寻找类似的解决方案了吗？为此，在 Google 窗口中输入 "电流镜"。和往常一样，相应的维基百科页面（过于正式和无聊）仍然在第一个位置。

那么让我们看看 Tony Kuphaldt 关于电流镜的页面。一开始，他正在讨论 Ebers-Moll 二极管方程。我们可以看到负载和晶体管，现在我们惊奇地喊道——这里有相同的二极管！Tony Kuphaldt 提出了我们同事也提出的建议——通过在基极-发射结并联连接一个正向偏置的二极管来改进电路。然后，作者开始讲述连接一个普通二极管的好处。

让我们仔细研究 Tony Kuphaldt 的电路，因为我有以下想法。因为他是一位非常优秀的老师和优秀的网络作家，我打算给他写一封电子邮件，描述我们的 Wikibooks “开放式学生项目”，并邀请他加入。更具体地说，我会告诉他，你和我和我们所有人是如何共同想到他的想法的；然后，我们如何检验它并发现它是正确的（或者不，现在我们必须决定）。这就是为什么判断他的电路非常重要的原因。

Tony 声称流过负载的输出电流等于流过二极管的输入电流：“因此，流过电阻 Rload 的电流是偏置电阻设定的电流的函数，两者几乎相等。”但这是真的吗？让我们试试。

谁会焊接？选择一个二极管，把它焊接到原型 PCB 上，并测量电流。据我记得，你的同事曾经说过，一个晶体管包含两个二极管。这里我们需要一个二极管，其 IV 曲线与驱动负载的晶体管的 IV 曲线相同。那么什么想法会产生呢？假设我们没有一个普通的二极管；我们只有晶体管...

一个基极-发射极晶体管“二极管”设定输入电流

用一个基极-发射极晶体管结替换真正的二极管

我们可以使用晶体管作为二极管吗？是的，我们可以。在这种情况下，我们可以连接一个相同晶体管的基极-发射极结（使集电极不连接）作为二极管。一名学生：是的，这是 Tony Kuphaldt 的下面那个电路...

他们经常使用这个“技巧”... 即使晶体管可以“半损坏”；我们只能使用它的一个结（在这种情况下，我们只需要基极-发射极结）。谁来画新的电路？让同事来画吧。让集电极不连接。尝试以更对称的方式绘制电路，并将其与基极转到另一个基极；这样我们更容易得到伟大的电流镜电路。最后，用绿色的电流回路画出电流流动的方向。所有的电流都从电源电压源的正极开始，并返回到负极。首先，一个输入电流从正轨下降，流过基极电阻，并到达两个基极之间的公共点。在这里，它撞击了两个并联连接的 PN 结（我们假设它们是相同的）。那么，它会做什么？电流将分成两个方向——向左和向右；有两个基极电流 I_B。

Tony Kuphaldt 的想法是什么？它断言，如果我们通过一个包含电阻和二极管（或充当电压稳定元件的基极-发射极结）的稳定器创建一个输入电压，并将此电压应用于另一个晶体管的基极-发射极结，则这两个电流（输入电流和输出电流）将几乎相等。简而言之，由于两个电压相等，因此两个电流相等。

然后寻找另一个但相同的晶体管并将其焊接。谁会来展示一下？只有，让我们在输入电路中连接另一个毫安表。我们可以期待这两个电流绝对相等吗？不，我们不能，因为两个晶体管不是绝对相同的；它们没有被选择。他们特别是在集成电路中制造了这种结构。谁会焊接？看看白板上的电路，并在原型板上实现它。不要移除串联连接到电位器的稳压电阻。它为什么在那里？当有人将电阻设置为零时，它可以保护晶体管的基极-发射极结。

顺便说一句，我从未做过这个实验；所以，我不知道会发生什么。结果可能是积极的，但也可能是消极的... 你对这些电流有什么看法？它们相等吗？好吧，我们稍后会检查它们。现在让我们整理一下测量设备。让电压表跨接在输出晶体管两端；我们需要它来知道晶体管是否处于有源区。两个毫安表将显示两个电流。

现在将输入电阻的滑块向上移动，增加输入电流。输出电流怎么样？它没有“移动”，保持不变（大约 2 mA）。为什么？测量输入电压（基极和发射极之间）以了解原因。正如我们所见，它大约为 0.65 V。这意味着什么？也许晶体管饱和了……为了确保，还要测量输出电阻上的电压 V_CE。您需要一个电压表；将电流表切换为电压表，并将其连接到第二个晶体管的集电极-发射极部分。只需要用一根导线闭合回路（使用两端有鳄鱼夹的导线）……

出现问题：晶体管冒烟了！

哦！晶体管开始冒烟了！它很热！但为什么？发生了什么？不可能！如果您的电路是白板上绘制的电路，晶体管不应该发热，因为在基极和集电极电路中连接了 3.9 kΩ 的“保护”电阻！还有其他原因，您必须找到它，因为它对我们非常有用。IMO，有些连接错误……您可以检查保护电阻，看它们是否是 3.9 kΩ。是的，它们是。

一个学生：我已经找到了原因 - 我们绕过了连接在集电极上的所有电阻！也许晶体管没有损坏？

好吧，让我们检查一下。唉！集电极-发射极之间没有电压；看来晶体管坏了。或者只是饱和了？

我们的实验结束了。您来自下一个小组 67b 的同事将继续您的工作。

（到这里，记录结束） 电路幻想家 2008 年 6 月 2 日 17:22 (UTC)

实验 4：运算放大器反相放大器

2008 年 4 月 22 日（星期二） 13.45

1.负反馈（NFB）原理

负反馈的主要思想是将输出 (Y) 返回到设备的输入 (X)（图 1）。换句话说，我们可以将这种想法理解为一种主动的“跟踪”或“跟随”。每个具有负反馈的设备都会“解决”方程X=Y。为了做到这一点，我们首先需要能量 (E)。另外，我们需要一个调节元件 (R) 来控制输出量Y。我们的 NFB 设备中的第三个元件是一个比较器 (-)，它将“分析”X 和Y 之间的差异，并将结果提供给调节元件，调节元件必须将差异降至零。

设备和系统使用 NFB 来补偿工作过程中可能发生的任何干扰。

图 1：[1]

2.电压跟随器

这是最简单的运算放大器配置。它跟随发送的电压。这是一个非常有用的小型电路。您可以使用它来保护电路免受过载。具有理想运算放大器的电压跟随器简单地给出 Vout = Vin。首先，我们有一个带有 NFB 的运算放大器：图 2：[2] 然后我们添加 2 个电阻：图 3：[3] 现在我们有了电压跟随器！！！

了解串联的 2 个电阻具有减去 2 个电压的能力是有益的：图 4：[4]。一个有趣的事实是，在尝试补偿干扰时，跟随器正在变成运算放大器。

这里我们可以看到理想电路中的一个电阻加法器：图 5：[5]

Yanita Petkova --闪耀的明星 (讨论) 2008 年 5 月 17 日 23:33 (UTC)

<<< 顶部 - 小组 64a - 小组 65a - 小组 66a - 小组 67a - 小组 68a - 页面阶段 >>>

<<< 小组 64b - 小组 65b - 小组 67b - 小组 68b >>>