电路构思/无源电流到电压转换器
电路构思: 通过电阻的电流使与电流成比例的电压降出现在电阻两端。

关于电路输入,我们更喜欢电压而不是电流作为输入量。唯一的例外是,一些设备具有电流输入(电流计、双极型晶体管、跨阻放大器、诺顿放大器等)。在这些情况下,我们在设备之前连接一个电压到电流转换器;结果,它获得了电压输入。
同样地,我们更喜欢电压而不是电流作为输出量。唯一的例外是,许多设备具有电流输出(实际上所有有源电子元件 - 电流源、双极型晶体管、电子管、场效应晶体管等)。在这些情况下,我们需要在设备之后连接反向电流到电压转换器,以获得电压输出。由于电流输出设备比电流输入设备更普遍,因此该电路比相反的电压到电流转换器更受欢迎。那么,让我们开始构建它吧!
与往常一样,该电路有两种版本 - 无源(“不好”)和有源(“好”);这里,我们从“不好”的无源版本开始。然后,在另一个专门介绍 “好”的有源版本 的故事中,我们将再次展示这两个电路之间存在密切的相互关系:有源版本源于无源版本(有源版本包含无源版本,它只是一个改进的无源版本)。通过这种方式,我们将展示著名的电路从简单到复杂的演变过程,一步一步地进行。
试图找到 上一个故事 中“什么导致什么?”这个问题的答案,我们假设压力导致流动。相反地,在我们日常生活中,有很多情况下流动导致压力。在这些情况下,移动的东西遇到了障碍;结果,出现了压力。以下是一些例子:机械(如果我们试图用我们的手阻止一辆移动的汽车,它会对我们施加压力),气动(想象一个恒流泵将空气通过一个封闭的管道环路 - 在中间夹紧软管,您会看到在瓶颈处出现了压力),社会(挡在某人的路上,您会体验到“压力”)等等。让我们最后概括所有这些情况。
为了引起压力,我们必须在流动路径上设置障碍。在这种安排下,类似流动、类似压力和类似阻碍的属性像以前一样相互关联。通常,输出的类似压力的变量与输入的类似流动的变量成比例;因此,我们可以说阻碍将类似流动的变量转换为类似压力的变量。

在电学中,我们可以观察到类似的电流导致电压现象:如果电流 IIN 通过电阻 R(图 2),后者会阻碍(抵抗)电流;结果,电阻两端出现与电流成比例的电压降 VR = R.IIN。[1] 在这个电流供电电路中,电压降 VR 充当输出电压 VOUT。唯一需要注意的是,电压降 VR 不是由电阻产生的;它是输入电流源内部的激励电压源产生的。我们可以说,这是欧姆定律的电流导致电压公式:V = R × I
在这个电流供电电路中,电阻 R 决定了它两端的电压。我们通常说,电阻将电流 IIN 转换为与之成比例的电压 VOUT,或者它充当简单的电流到电压转换器 - 一个具有传递比 k = VOUT/IIN [V/mA] 的线性电路。
如果我们用电压条和电流环路(图 2)来可视化看不见的电量,我们可以比 V = R × I 更具吸引力地展示电路操作和欧姆定律。如果您还记得,在这个“几何”表示中,电流环路的厚度与电流的大小成比例,电压条的高度与相应的电压或压降成比例(另见一个交互式 动画)。
然后,我们可以用图解分析法(图 3)来展示电路操作(和欧姆定律)。由于两个 2 端器件(电压源和电阻)两端的电压和通过它们的电流相同,我们可以将它们的 IV 曲线叠加在同一个坐标系上。两条线的交点是工作点 A;它表示电流 IA 和电压 VA 的大小。
当我们改变输入电流源的电流时,它的 IV 曲线会垂直移动(另见一个交互式 动画)。结果,工作点 A 在电阻 R 的 IV 曲线上滑动;它的斜率表示转换器的比例。


与以前一样,我们还可以使用欧姆定律的引人入胜的图形解释,称为电压图(线性电阻内部电阻薄膜上的电压分布,图 4)。这里,当输入电流变化时,电阻薄膜上的局部电压会逐渐从左到右减小(另见另一个交互式 动画)。在这种安排下,角度 α 表示输入电流 IIN。

电流控制电压源。 虽然自然界中存在足够的恒压源(例如,原电池和蓄电池),但如果我们拥有一个电流源而需要一个电压源,我们可以将其构建出来。 为此,我们在电流源之后连接一个电流到电压转换器。
电压源 = 电流源 + 电流到电压转换器
这意味着只需将一个简单的电阻器 R 并联连接到输入电流源 IIN(诺顿定理在电力中的应用) - 图 5。
如果负载是理想的(即,其具有无穷大的电阻),该复合电压源将产生一个恒定的电压 VOUT = R.I。 此电压将影响电流,如果输入电流源不完美(请参见 缺陷)。

复合无源转换器: 同样地,在常用的无源电路中,例如电容微分器、电感积分器、反对数转换器等,电阻器充当电流到电压转换器。
V-to-V CR 微分器 = V-to-I C 微分器 + I-to-V 转换器
V-to-V LR 积分器 = V-to-I L 积分器 + I-to-V 转换器
V-to-V DR 反对数转换器 = V-to-I D 反对数转换器 + I-to-V
例如,图 6 中的经典电容-电阻微分器是通过使用更简单的电压到电流电容微分器(一个裸露的电容器)和一个电流到电压转换器构建的。
在这些电路中,相应的 I-to-V 转换器会引入一些压降,这会影响激励电压 VIN。 结果,电流减小,出现误差(请参见有关 缺陷 的部分)。

晶体管集电极电阻。 结型双极晶体管是一种产生电流的器件。 因此,为了获得电压作为输出,在晶体管级的输出电路中连接了一个集电极电阻。 此技术的示例包括共射极放大器、共基极放大器和差动放大器、晶体管开关等。
电压输出晶体管 = 电流输出晶体管 + I-to-V 转换器
晶体管的集电极电阻充当电流到电压转换器。
由于压降 VRc 是浮动的,通常使用与电源互补的压降 VCE 作为输出。 结果,这些晶体管电路是反相的(当输入电压升高时,输出电压下降,反之亦然)。
类似的技术用于在负反馈电流源的晶体管发射极获得电压。 此技术的示例包括所有使用串联负反馈的晶体管电路。
晶体管的发射极电阻充当电流到电压转换器。

复合电流表。 如今的测量仪器(数字电压表、模数转换器等)主要是伏特表。 如果需要测量电流,我们会在伏特表之前连接一个简单的电流到电压转换器(分流电阻)。 该电流表是一个由两个组件组成的复合器件。
复合电流表 = 电流到电压转换器 + 伏特表
复合电流表的 shunt 电阻充当电流到电压转换器。
虽然有源版本是完美的电流测量解决方案,但常用的万用表使用的是无源版本来测量大电流(请参见功率考虑因素)。


同样地,使用负反馈构建的运算放大器电压到电流转换器(电压控制恒流源)实际上是一个反向的电流到电压转换器。 我们可以将其作为晶体管版本(图 9)或作为电流源的运算放大器版本(图 10)来实现。 在这些电路中,我们在负反馈回路中连接一个电流到电压转换器(裸露的电阻器 R)。 然后,为了比较与负载电流 I 成正比的压降 VR 与输入电压 VZ,我们将这两个电压串联连接,并将它们的差值 dV = VZ - VR 应用于调节元件(晶体管 T 的基极-发射极结或运算放大器 OA 的差分输入)的输入部分。 结果,调节元件通过改变其输出电阻来建立电流 I = VR/R ≈ VZ/R,从而使电压差 dV 为零。 这样,输出电流与输入电压成正比;整个电路充当电压到电流转换器。

您还记得我们在考虑相反的电压到电流转换器时,我们调查了输入和输出电阻吗? 让我们对当前的电流到电压转换器做同样的事情。 为了具体起见,假设有一个电阻性负载 RL。
输入电阻是多少? 首先,将一个电流表串联连接到转换器的输入端,将一个伏特表并联连接到转换器的输入端;然后,改变输入电流以调查输入电阻。 从输入源的角度看,我们看到了两个并联连接的电阻器 - R 和 RL;因此,输入电阻是 RIN = R||RL。 如您所见,它取决于负载电阻 RL。 不过,我们选择 R << RL;因此,RIN ≈ R。
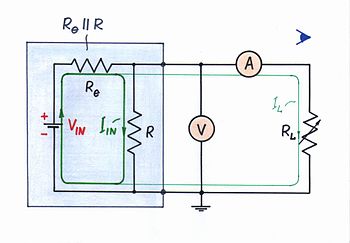
输出电阻是多少? 现在,将一个伏特表并联连接到转换器的输出端,将一个电流表串联连接到转换器的输出端;然后,改变负载电阻(电压)并观察电流以调查输出电阻。 从负载的角度看,我们看到了两个并联连接的电阻器 - Re(输入电路的等效电阻)和 R;因此,输出电阻是 ROUT = Re||R。 如果输入电流是由理想电流源产生的,则输出电阻仅为 ROUT ≈ R。

问题。 不过,这里出现了一个奇怪的矛盾。 一方面,电阻器 R 上的压降 VR 对我们是有用的(这是我们需要的输出电压!)。 另一方面,这种压降是麻烦的,因为它会削弱激励电压 VIN(这里我们假设输入电流是由电压源 VIN 通过电阻器 Ri 产生的)。 现在,电压差 VIN - VR 决定了电流,而不是电压 VIN。 事实证明,测量电流会导致干扰! 结果,电流 IIN 减少:我们该怎么做才能解决这个矛盾?
如果您在交互式 Flash 动画 [2] 中单击“探索”按钮,或者如果您转到交互式 Flash 构建器 的“阶段 2”,可以以更具吸引力的方式探索电路运行。[3]
经典补救措施。 我们可以通过降低电阻器 R 的电阻来减小其引起的误差。 不过,输出电压也会降低,我们可能需要对其进行放大。 这样做,我们也会放大噪声...... 那么如何解决这个问题呢?
寻找完美的补救措施。 显然,我们必须解决这个矛盾,使电阻器 R 既存在又不存在! 我们如何实现这种魔法呢? 一个提示:记住当生活中出现糟糕的事情时,我们通常会怎么做。 如果您无法找到补救措施,请访问有关 有源电压到电流转换器 的相关故事以获取答案。
无源电流到电压转换器比相反的 无源电压到电流转换器 更受欢迎。 它在电子学书籍和网络资源中都有很好的介绍。 以下是一些例子。
- ↑ 具有电压输出的基本无源转换器 是一个关于产生电流的最简单电子转换器的教师故事。
- ↑ 无源电流到电压转换器 是一个揭示无源版本哲学的动画 Flash 教程。
- ↑ 运算放大器电路构建器 (动画哲学) 是一个交互式 Flash 教程,演示了如何将任何无源转换器转换为有源转换器。
电路理念 (本书)
无源电压到电流转换器揭示了相反无源电路背后的基本原理。
运算放大器反相电压到电流转换器的再发明揭示了相反有源电路背后的基本原理。
电流到电压转换器介绍了电路的无源和有源版本。
电压到电流转换器介绍了“镜像”电路的无源和有源版本。
电气和电子工程师如何使用欧姆定律是关于电气属性之间关系的有趣故事。
电流到电压转换器的再发明是一个类似的电路故事,但结构更好,更易于浏览。
跨阻放大器的再发明是一个专门针对有源版本的 story。
我们如何构建一个运算放大器电流表?是关于更简单的有源版本类似的故事。
电阻器和 晶体管表明集电极电阻可以作为简单的电流到电压转换器(图解和动画效果很好)。
