电路理论/联立方程/示例 1

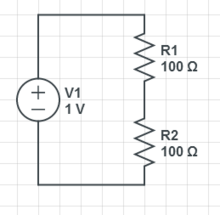
原始示例 1 电路

求解所有未知电压和电流。

标注

示例 1 电路，标注了电压和电流，1 个回路，无节点

目标是标记未知量和已知量。原始问题已创建符号 $V1,R1{\text{ and }}R2$ 并赋予它们值。它们似乎是已知量。此时标记的未知量为 $i_{1},v_{R1}{\text{ and }}v_{R2}$.

此处显示相关源方程。

回路

该电路中有一个回路。它以顺时针方向绘制，在直线上添加一个箭头，并在回路上添加符号 $L_{1}$。此符号将是来自此箭头的回路方程的名称。

接下来，在电阻器上添加与电压相关的 + 和 -，以指示电路中的极性关系（从绘制的回路开始）。

重要的是要记住，在这一点上，+ 和 - 以及回路都包含电路拓扑信息。它们不是对最终数值答案的“猜测”。

节点

该电路中没有节点。有三个微不足道的节点，但所有三个节点的电流都相同。此时选择电流方向。

此时选择电流方向。现在，在图纸上添加箭头以指示方向。它不是任意的。电流必须流入组件的 + 端并流出 - 端。

电压电源的 + 端的电流是流出还是流入并不重要，因为电压电源会根据电路的其余部分改变其电流。

方程计数

第一步是列出变量以及它们是已知量还是未知量。
$V_{1}=1volt$
$R_{1}=100ohm$
$R_{2}=100ohm$
$i_{1}=?amp$
$v_{R1}=?volt$
$v_{R2}=?volt$

因此，有三个未知量，需要三个方程。

端点方程

有两个器件可以写出端点方程
$TR1:v_{R1}=i_{1}*R_{1}$
$TR2:v_{R2}=i_{1}*R_{2}$

电源没有端点方程。

回路方程

只有一个回路方程
$L1:v_{R1}+v_{R2}-V_{1}=0$

电源电压为负，因为回路方向进入电源负极。

节点方程

没有节点，因此没有节点方程。如果要统计三个平凡节点，将会有三个电流：分别流过每个元件（两个电阻和电源）。这时需要写下三个平凡方程，说明它们彼此相等（取决于方向）。下一个例子将探索节点。

求解方程

三个方程为
${\begin{cases}TR1:{\text{ }}v_{R1}=i_{1}*R_{1}\\TR2:{\text{ }}v_{R2}=i_{1}*R_{2}\\L1:{\text{ }}v_{R1}+v_{R2}-V_{1}=0\end{cases}}$

代数

求解方案概述

• 将 TR:1 和 TR:2 代入 L1:，求解未知量 $i_{1}$
• 将电流解代入 TR:1 和 TR:2，求解未知量 $v_{R1}v_{R2}$
• 将已知值代入符号以获得数值解

代数符号解

• $i_{1}={\frac {V_{1}}{R_{1}+R_{2}}}$
• $v_{R1}={\frac {V_{1}*R_{1}}{R_{1}+R_{2}}}$
• $v_{R2}={\frac {V_{1}*R_{2}}{R_{1}+R_{2}}}$

代数数值解

• $i_{1}={\frac {1}{100+100}}={\frac {1}{200}}=0.005amp$
• $v_{R1}={\frac {1*100}{100+100}}={\frac {100}{200}}={\frac {1}{2}}=0.5volt$
• $v_{R2}={\frac {1*100}{100+100}}={\frac {100}{200}}={\frac {1}{2}}=0.5volt$

这是一个简单的例子。但我们的目标是练习所有数学工具。将来这些工具中的一种或多种可能会失效。我们的目标是现在体验使用这些工具的成功，这样我们就知道失败是什么样子的。

微分方程

在本例中没有微分方程，但本课程有四分之三时间在讨论这种复杂的电路，使用电容和电感代替电阻，并查看微分方程。

符号计算

Wolfram Alpha

File:Ex1wolf.png

Mathematica 对示例 1 的解决方案

点击上面的链接，进入 Wolfram 网站，查看输入的语法和答案。注意以下几点

• Wolfram Alpha 处理不了“i”，它可能认为它是一个虚数。所以需要切换到“k”。
• Wolfram Alpha 处理不了双下标，所以需要从 R1 切换到 2，从 R2 切换到 3。

一个不能解释我们符号的自然语言符号解释器有什么意义？如果我们必须将我们的符号映射到它理解的符号，为什么不直接使用 MatLab 矩阵（线性代数）呢？

Mathematica

Mathematica 与 Wolfram Alpha 有关（Alpha 表示非常早期的、粗略的草稿）。它可以工作。但看看解决方案

• 必须学习另一种标记语言
• 仍然存在下标问题

真正的问题是，用最少的按键、最少的错误、最少的符号组织或映射可以做些什么？

Mathematica 应该得到认可，因为它尝试了这种类型的符号解释和计算。其他软件包，如已停产的“TI Derive”，不支持任何下标。但 MathWorks 的符号（MuPAD）和数值（MatLab）目前提供了最佳的组合。Wolfram Alpha 为学生开始符号计算降低了门槛。这里的目标是找出它在哪里失效。本文将重点介绍 MathWorks 产品。

MuPad

File:Ex1matlab3.png

MathWorks MuPAD 解决方案 .. 点击 这里 获取可以剪切和粘贴的文本 .. MuPAD 解决方案包含变量解决方案、符号解决方案和数值解决方案

MatLab 具有一个添加符号支持的符号包。启动 MatLab，然后输入“MuPad”。上面的方程可以输入到 MuPAD 中，然后可以使用变量符号、精确常数和数值近似值（小数位数）来求解方程。

数值解

File:Ex1matlab4.png

Matlab 矩阵输入，用于求解三个方程三个未知数的线性代数问题 .. 点击 这里 剪切粘贴

File:Ex1mathematica2.png

Mathematica 矩阵输入和求解三个方程三个未知数的线性代数问题。点击 这里 剪切粘贴。

设置解决方案的步骤

• 将已知值代入方程

${\begin{cases}TR1:{\text{ }}v_{R1}=100*i_{1}\\TR2:{\text{ }}v_{R2}=100*i_{1}\\L1:{\text{ }}v_{R1}+v_{R2}-1=0\end{cases}}$

• 将方程整理，使未知数在列中，数字在等号的右侧

${\begin{cases}TR1:{\text{ }}v_{R1}+0-100*i_{1}=0\\TR2:{\text{ }}0+v_{R2}-100*i_{1}=0\\L1:{\text{ }}v_{R1}+v_{R2}+0=1\end{cases}}$

• 创建两个矩阵，一个是方阵，另一个是列向量，其中包含等号右侧的数字

${\begin{array}{|c|c|c||c|}v_{R1}&v_{R2}&i_{1}&=\\\hline 1&0&-100&0\\0&1&-100&0\\1&1&0&1\\\end{array}}$

$\Rightarrow$

${\begin{bmatrix}1&0&-100\\0&1&-100\\1&1&0\end{bmatrix}}$

$\bullet$

${\begin{bmatrix}V_{R1}\\V_{R2}\\i_{1}\end{bmatrix}}$

=

${\begin{bmatrix}0\\0\\1\end{bmatrix}}$

• 将矩阵输入到MatLab或类似的程序中

${\begin{bmatrix}V_{R1}\\V_{R2}\\i_{1}\end{bmatrix}}$

=

${\begin{bmatrix}0.5\\0.5\\0.005\end{bmatrix}}$

模拟

目标是在www.circuitlab.com中模拟。点击此链接，然后点击底部的模拟按钮。将笔移到电路周围。

电阻：电流为5ma，正如预测的那样。注意电流的符号。它在-和+ 5 ma之间变化。当电流进入电阻的顶部（A）时，看起来是正的，因为电压是正的。这使得电流为正。

电压相对于地。电源顶部的电压和电阻顶部的电压相同，因为它们是同一平凡结的一部分。电压为1伏，因为它是两个电阻之间的电压。底部电阻上的电压是预测的一半。

电源：电源的相反情况也是如此。电流从电源的顶部（A）流出，标记为负。从任何东西的+端流出的电流都是负的。

功率计算

电压和电流是恒定的。

• $P=i*v$
• $P_{source}+P_{R1}+P_{R2}=0$
• $(-.005)*1+(.005)*.5+(.005)*.5=0$

建立直觉

这是一个简单的电路，展示了物理学中涵盖的概念。

• 串联的等值电阻将它们之间的电压分配。
• 串联的电阻分配电压。
• 串联电阻相加。