电路理论/联立方程/示例 5

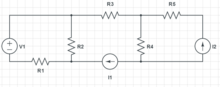
求解电流和电压。假设电源和电阻值已知。用符号解。

从实际角度来看，在一个电路中放置多个电源是不好的做法。几乎所有人都试图设计只使用一个电源的电路。

从建模的角度来看，晶体管在一级近似中是一种电源。因此，在一个电路中放置多个电源是一种实践或为更复杂的电路做准备。

标记

有一个电压源，串联一个电阻，以获取其电流： $i_{R1}$ 。两个电流源没有与它们并联的明确电阻，因此必须标记每个电流源的电压： $i_{I1}$ 和 $i_{I2}$ 。

回路

有三个回路。请记住，现在的 + 和 - 不是在猜测答案的极性，而是在捕捉电路的布局。

没有无意义回路（并联元件）。

节点

有两个无意义节点，串联元件共享相同的电流。一个是电压源和 $R_{1}$ 之间。另一个是电流源 $I_{2}$ 和 $R_{5}$ 之间。

有四个非无意义节点，请查看以不同颜色阴影显示的恒定 EMF 区域。

这意味着可以使用三个节点。选择哪三个并不重要。但是必须选择三个，然后将电流相对于电阻上的电压极性放置。电流源所在的两个分支不需要为它们创建额外的电流符号，就像电压源不需要为它创建电压符号一样。

方程计数

我们被告知电阻和电压源有值，因此应该被视为已知数。我们只是不知道具体的值是多少，所以我们必须用符号来解。

$R_{1}=\surd$
$R_{2}=\surd$
$R_{3}=\surd$
$R_{4}=\surd$
$R_{5}=\surd$
$I_{1}=\surd$
$I_{2}=\surd$
$V_{1}=\surd$
$i_{R1}=?$
$i_{R2}=?$
$i_{R3}=?$
$i_{R4}=?$
$v_{R1}=?$
$v_{R2}=?$
$v_{R3}=?$
$v_{R4}=?$
$v_{R5}=?$
$v_{I1}=?$
$v_{I2}=?$

共有 11 个未知数。由电阻可得 5 个方程，由回路可得 3 个方程，由节点可得 3 个方程。因此，该问题可显式求解。

端子方程

$v_{R1}=i_{R1}*R_{1}$
$v_{R2}=i_{R2}*R_{2}$
$v_{R3}=i_{R3}*R_{3}$
$v_{R4}=i_{R4}*R_{4}$
$v_{R5}=-I_{2}*R_{5}$
电流 $I_{2}$ 为负，因为它流入 $R_{5}$ 的负极。

当有多个电源时，方程式必须包含其电流方向或电源极性。

如果方向弄错了，通常答案的大小会正确，但符号会错误。关键是答案非常相似。问题通常是符号约定以某种方式弄乱了。

环路方程

$L_{1}:v_{R2}+v_{R1}-V_{1}=0$
$L_{2}:v_{R3}+v_{R4}+v_{I1}-v_{R2}=0$
$L_{3}:v_{R5}+v_{I2}-V_{R4}=0$

电流源的电压极性是任意选择的，但必须做出选择。必须在图纸上记录选择，然后反映在方程式中。否则无法检查方程式。

节点方程

$J_{1}:i_{R1}-i_{R2}-i_{R3}=0$
$J_{2}:i_{R3}+I_{2}-i_{R4}=0$
$J_{3}:i_{R4}-I_{2}-I_{1}=0$

求解方程组

代数

代数解法非常庞大、混乱，难以检查，而且不会激发任何人的兴趣。不会尝试它。

微分方程

这个问题中没有微分方程，但本课程四分之三的时间都在学习这种复杂电路，使用电容器和电感器而不是电阻器，并观察微分方程。

符号计算

Mathematica

文件：Ex5-6.png

Mathematica 解法。点击此处获取要输入 Mathematica 的文本。

无论方程的形式如何，Wolfram Alpha 都不支持超过 6 或 7 个方程。将在 Mathematica 中进行。然后在 MuPAD 中进行。然后比较答案。

MuPAD

文件：Ex5-7.png

MathWorks MuPAD 解法 .. 点击此处获取要剪切和粘贴的文本 .. MuPAD 解法包含变量解

MuPAD 的答案与 Mathematica 相匹配，但更复杂答案的格式截然不同。然后目标是使用某种简化命令，但可以使用替代符号来表达相同的答案。查看 $V_{I2}$ 答案。它们相同，但它们使用不同的符号。

事实上，还有一个答案

$V_{I1}={\frac {(R_{1}+R_{2})}{R_{1}*R_{2}}}*({\frac {V_{1}}{R_{1}}}-I_{1})-R_{3}*I_{1}-R_{4}*(I_{1}+I_{2})$

文件：Ex5-7r.png

使用简化命令简化的 Mathematica 解法 .. 看起来更接近 MuPAD 解法

使用简化和扩展命令进行一些操作会有所帮助。与简化命令相关的各种选项引入了符号计算的领域，这会使本课程的重点偏离。对于复杂表达式的求解，各软件包之间还没有达成一致意见。除 $V_{I1}$ 之外，所有内容的视觉检查都是匹配的。

唯一其他快速检查方法是代入一组随机数，看看两个解是否得出相同的数值解。但在这方面已经花费了足够的时间。

数值解

由于没有给出数字，所以不存在数值解。

模拟

没有数字，模拟是不可能的。

建立直觉

复杂的表达式没有符号计算一致同意的通用形式。因此，检查它们是一个代数过程，或者可以相信，插入数字并显示它们匹配意味着符号表达式是相同的。
当定义变量时，方向选择暗示 $V_{1}$ 正在向电路中注入能量。观察解，似乎 $I_{R1}$ ，即通过 $V_{1}$ 的电流是正的。因此，仍然是 $V_{1}$ 正在向电路中注入能量。
当定义变量时，方向选择暗示 $I_{2}$ 正在向电路中注入能量。观察解，似乎 $V_{I2}$ ，即跨过 $I_{2}$ 的电压是正的。因此，仍然是 $I_{2}$ 正在向电路中注入能量。
当定义变量时，方向选择暗示 $I_{1}$ 正在从电路中吸收能量并为其电池充电。然而，观察解，似乎 $V_{I2}$ ，即跨过 $I_{1}$ 的电压是负的。因此，看来实际上 $I_{1}$ 也正在向电路中注入能量。