电路理论/状态变量

需要新的技术来解决二阶及更高阶电路

• 符号解太复杂，仅仅比较答案也是一个练习
• 解析解法更加零散
• 常数、初始条件和电路布局之间的关系变得复杂

如果电路分析要

• 超越理想
• 考虑更复杂的电路
• 了解电路建模软件的局限性/近似值

解决方案是“状态变量”。在状态变量分析之后，通过消除对输出影响不大的项，可以简化创建符号解的过程。

状态空间

电路理论的 状态空间 方法放弃了电路分析的符号/解析方法。状态变量模型涉及以矩阵形式描述电路，然后使用 级数展开、辛普森规则 和 克莱姆法则 等工具进行数值求解。这是 matlab 的最初起点。

状态

“状态”表示电路能量存储元件的“条件”或“状态”。由于电阻器不会改变（理想情况下）并且不存储能量，因此它们不会改变电路的状态。状态是在时间上的一个快照，代表着电流和电压。 “状态空间”分析的目标是创建一种表示所有可能状态的符号。

状态变量

用于描述所有状态的符号应该尽可能简单。与其试图找到一个复杂的、高阶的微分方程，不如回到类似于 基尔霍夫分析 的东西，并只写端子方程。

状态变量是电容器两端的电压和电感器中的电流。这意味着纯电阻电路的 割集 被合并成单个电阻器，最终与电感器串联或与电容器并联。与其使用符号 v 和 i 来表示这些未知数，不如将它们都称为 x。使用基尔霍夫方程代替节点方程或回路方程。端子方程被代入基尔霍夫方程，这样剩余电阻的电流和电压就会与电感器和电容器共享。

状态空间模型

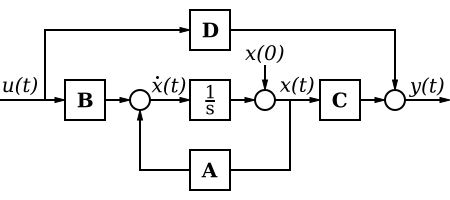
此状态空间模型描述了输入（阶跃函数 μ(t)、初始条件 X(0)）、输出 Y(t) 以及 A、B、C 和 D。A-B-C-D 是传递函数，它们以如下方式组合

${\frac {\mathbb {Y} }{\mathbb {\mu } }}=B(s)\left({\frac {1}{s-A(s)}}\right)C(s)+D(s)$

控制系统课程教导如何从所需的传递函数构建这些框图。积分“记忆”或累积过去状态的历史。导数预测未来状态，此外，当前状态可以分别进行缩放。“A”表示反馈。“D”表示前馈。还有很多东西要学。

不要试图弄清楚负号是如何出现在分母中的，以及附加项是如何出现的。上面是如何帮助我们预测电路中的电压和电流？让我们从定义术语并举一些例子开始。

• A 是一个方矩阵，表示电路元件（来自基尔霍夫方程）。
• B 是一个列矩阵或向量，表示源如何影响电路（来自基尔霍夫方程）。
• C 是一个行矩阵或向量，表示输出是如何计算的（可能是电压或电流）
• D 是一个单一数字，表示源的倍数...... 通常为零，除非源直接通过电阻器连接到输出。

A 和 B 一般描述电路。如果 X 是一个列矩阵（向量），表示所有未知的电压和电流，那么

${\boldsymbol {\dot {X}}}={\boldsymbol {A}}{\boldsymbol {X}}+{\boldsymbol {B}}{\boldsymbol {\mu }}$

此时，X 已知，表示时间函数的列。可以使用 C 和 D 从已知的 X 和原始阶跃函数 μ 推导出输出

$y={\boldsymbol {C}}{\boldsymbol {X}}+D*{\boldsymbol {\mu }}$

MatLab 实现

文件：MatLabSimulinkStateSpace.png

matlab 屏幕截图，带有 simulink 工具箱，显示如何获取用于维基教科书电路分析的状态空间块

如果没有像 MatLab 这样的工具，这将不会是一个进步。这些是相关的 MatLab 控制系统工具箱命令

• step(A,B,C,D) 假设初始条件为零
• initial(A,B,C,D,X(0)) 与 step 相同，但考虑了初始条件 X(0)

此外，还有一个名为“状态空间”的 simulink 块，可以用相同的方式使用。

视频介绍

• 来自 digilent corp 的 41 分钟介绍
• 5 分钟电路应用

进一步阅读

• 控制系统/状态空间方程
• matlab 帮助链接