数字信号处理/数字滤波器

数字信号处理

数字滤波器可以是非常复杂的设备，但它们必须能够映射到滤波器设计的差分方程。这意味着，由于差分方程只有有限数量的操作可用（加法和乘法），数字滤波器也只有有限的操作需要处理。数字滤波器只有少数几个基本组件，尽管这些组件可以以复杂的方式排列以创建复杂的滤波器。

数字滤波器类型

数字领域中有两种类型的滤波器：有限脉冲响应（FIR）滤波器和无限脉冲响应（IIR）滤波器。它们本质上截然不同。

FIR 滤波器

FIR 滤波器是采样系统的特有滤波器。连续时间系统中没有等效的滤波器。因此，只有非常特殊的模拟滤波器能够实现 FIR 滤波器。

如果我们将离散时间冲激函数定义为

\delta [n]={\begin{cases}1&n=0\\0&n\not =0\end{cases}}{\mbox{,}}

FIR 滤波器对 δ[n] 的响应，记为 h[n]，将在有限数量的样本后衰减为零。FIR 滤波器的传递函数只包含零点，或者没有极点，或者只有位于原点的极点。

具有对称系数的 FIR 滤波器保证提供线性相位响应，这在某些应用中非常重要。然而，FIR 滤波器的效率较低，要创建满足给定规格的 FIR 需要比等效 IIR 滤波器多得多的硬件。

IIR 滤波器（无限脉冲响应滤波器）

IIR 滤波器通常基于连续时间传递函数设计。IIR 滤波器不同于 FIR 滤波器，因为它们始终包含电路中的反馈元件，这使得传递函数更难处理。

IIR 滤波器的传递函数包含极点和零点。它的冲激响应永远不会衰减为零（尽管它可能非常接近零，以至于响应无法用系统中可用的位数表示）。

IIR 滤波器在计算方面提供了非凡的好处：IIR 滤波器的效率比等效 FIR 滤波器高一个数量级以上。尽管 FIR 滤波器更容易设计，但 IIR 滤波器可以用更少的组件完成相同的工作，更少的组件直接转化为更少的成本。

在 Octave/Sciplot 中对时间序列进行滤波

首先为时间序列创建一些点。在本例中，我们将创建以 44 kHz 采样的一秒钟随机数据。

sampling_t = 1/44000;
t = 0:sampling_t:1;
x = rand(size(t));

查看时间序列

plot(t,x);

查看它的频谱（它大多是均匀的，这是我们对噪声的预期结果）

specgram(x)

现在，我们将使用内置函数创建一个截止频率为 pi*0.1 弧度的三阶巴特沃斯低通滤波器

[b,a] = butter(3,0.1)

现在对时间序列进行滤波。

y = filter(b,a,x);

查看滤波后数据的首 100 个点。

 hold on
 plot(y(1:100))
 plot(x(1:100))
 hold off

检查它的频谱图

 specgram(y)

现在查看 FFT 的幅度

 plot(log(abs(fft(y))))

滤波器响应类型

高通和低通

高通和低通滤波器是最简单的数字滤波器形式，它们相对容易设计到规格。本页将讨论高通和低通传递函数，以及每种传递函数作为 FIR 和 IIR 设计的实现。

带通

带通滤波器就像高通滤波器和低通滤波器的组合。只有特定频带允许通过滤波器。过高或过低的频率将被滤波器抑制。

阻带

陷波滤波器是带通滤波器的补充，它只抑制特定窄频带的频率信息，并允许所有其他数据毫无问题地通过。

陷波

带通滤波器的直接补充称为带阻滤波器。陷波滤波器本质上是一个非常窄的带阻滤波器。

梳状滤波器

梳状滤波器顾名思义，看起来像一把梳子。它们有很多“齿”，本质上是在传递函数中信息被去除的陷波。这些陷波均匀地分布在整个频谱中，因此它们只对消除以规则频率间隔出现的噪声有用。

全通

全通滤波器是一个对所有频率具有单位幅度响应的滤波器。它不影响系统的增益响应。全通滤波器确实会影响系统的相位响应。例如，如果设计 IIR 滤波器以满足规定的幅度响应，系统的相位响应通常会变得非线性。为了校正这种非线性，将全通滤波器级联到 IIR 滤波器中，以便整体响应（IIR+全通）具有恒定的群延迟。

典型和非典型

正则滤波器是指传递函数的阶数与滤波器中延迟单元数量相同的滤波器。相反，非正则滤波器是指滤波器中延迟单元数量多于传递函数的阶数的滤波器。一般来说，FIR 滤波器是正则的。一些 IIR 滤波器实现是非正则的。

以下是一个 2 阶正则滤波器的例子。

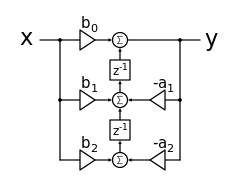
以下是一个 2 阶非正则滤波器的例子。

注意，在正则滤波器中，系统阶数（这里为 2）等于滤波器中的延迟单元数量（2）。在非正则版本中，系统阶数不等于延迟单元数量（4 个延迟单元）。两种滤波器执行相同的功能。正则版本在数字硬件上更小，因为它使用的延迟单元更少。然而，如果级联多个二阶 IIR 滤波器，这种缺点几乎消失，因为它们可以共享延迟单元。在这种情况下，唯一的“额外”延迟单元是第一级输入侧的那些。

符号

我们将使用一些基本符号。

ω_p 通带截止频率

ω_s 阻带截止频率

δ_p 通带纹波峰值幅度

δ_s 阻带纹波峰值幅度

← 快速傅里叶变换 (FFT) 算法

数字信号处理

FIR 滤波器设计 →