数字信号处理/FIR滤波器设计

数字信号处理

滤波器设计

设计过程通常从所需的传递函数幅度开始。拉普拉斯逆变换以采样值的形式提供冲激响应。

冲激响应的长度也称为滤波器阶数。

理想低通滤波器

理想（砖墙或sinc滤波器）低通滤波器的冲激响应形式为sinc函数

h(n)={\frac {\omega _{c}}{\pi }}{\frac {sin(\omega _{c}n)}{\omega _{c}n}}

此函数长度无限。因此它无法在实践中实现。但是它可以通过截断来近似。相应的传递函数在截止频率过渡阶跃的两侧波动。这被称为吉布斯现象。

窗函数设计法

为了平滑截止频率附近的传递函数波动，可以用连续函数（如汉明窗、汉宁窗、布莱克曼窗和更多形状）代替砖墙形状。这些函数也称为窗函数，也用于在处理之前平滑一组样本。

以下代码说明了汉明窗FIR的设计

#!/usr/bin/python3

import math
import numpy as np
import scipy.signal as sig
import matplotlib.pyplot as plt

# ------------------------------------------------------------------------------
# Constants
#
                                                                        # filter
signal_bit_nb = 16
coefficient_bit_nb = 16
sampling_rate = 48E3
cutoff_frequency = 5E3
filter_order = 100
                                                                   # time signal
input_signal_duration = 10E-3
frequency_1 = 1E3
amplitude_1 = 0.5
frequency_2 = 8E3
amplitude_2 = 0.25
                                                                       # display
plot_time_signals = False
plot_transfer_function = False
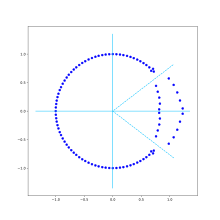
plot_zeros = True
input_input_signal_color = 'blue'
filtered_input_signal_color = 'red'
transfer_function_amplitude_color = 'blue'
transfer_function_phase_color = 'red'
locus_axes_color = 'deepskyblue'
locus_zeroes_color = 'blue'
locus_cutoff_frequency_color = 'deepskyblue'

#-------------------------------------------------------------------------------
# Filter design
#
Nyquist_rate = sampling_rate / 2
sampling_period = 1/sampling_rate
coefficient_amplitude = 2**(coefficient_bit_nb-1)

FIR_coefficients = sig.firwin(filter_order, cutoff_frequency/Nyquist_rate)
FIR_coefficients = np.round(coefficient_amplitude * FIR_coefficients) \
    / coefficient_amplitude

transfer_function = sig.TransferFunction(
    FIR_coefficients, [1],
    dt=sampling_period
)

# ------------------------------------------------------------------------------
# Time filtering
#
sample_nb = round(input_signal_duration * sampling_rate)
                                                                   # time signal
time = np.arange(sample_nb) / sampling_rate
                                                                  # input signal
input_signal = amplitude_1 * np.sin(2*np.pi*frequency_1*time) \
    + amplitude_2*np.sin(2*np.pi*frequency_2*time)
input_signal = np.round(2**(signal_bit_nb-1) * input_signal)
                                                               # filtered signal
filtered_input_signal = sig.lfilter(FIR_coefficients, 1.0, input_signal)
                                                                  # plot signals
if plot_time_signals :
    x_ticks_range = np.arange(
        0, (sample_nb+1)/sampling_rate, sample_nb/sampling_rate/10
    )
    y_ticks_range = np.arange(
        -2**(signal_bit_nb-1), 2**(signal_bit_nb-1)+1, 2**(signal_bit_nb-4)
    )

    plt.figure("Time signals", figsize=(12, 9))
    plt.subplot(2, 1, 1)
    plt.title('input signal')
    plt.step(time, input_signal, input_input_signal_color)
    plt.xticks(x_ticks_range)
    plt.yticks(y_ticks_range)
    plt.grid()

    plt.subplot(2, 1, 2)
    plt.title('filtered signal')
    plt.step(time, filtered_input_signal, filtered_input_signal_color)
    plt.xticks(x_ticks_range)
    plt.yticks(y_ticks_range)
    plt.grid()

#-------------------------------------------------------------------------------
# Transfer function
#
                                                             # transfer function
(w, amplitude, phase) = transfer_function.bode(n=filter_order)
frequency = w / (2*np.pi)
                                                        # plot transfer function
if plot_transfer_function :
    amplitude = np.clip(amplitude, -6*signal_bit_nb, 6)

    log_range = np.arange(1, 10)
    x_ticks_range = np.concatenate((1E2*log_range, 1E3*log_range, [2E4]))
    amplitude_y_ticks_range = np.concatenate((
        [-6*signal_bit_nb], 
        np.arange(-20*math.floor(6*signal_bit_nb/20), 1, 20)
    ))
    phase_y_ticks_range = np.concatenate((
        1E1*log_range, 1E2*log_range, 1E3*log_range
    ))

    plt.figure("Transfer function", figsize=(12, 9))
    plt.subplot(2, 1, 1)
    plt.title('amplitude')
    plt.semilogx(frequency, amplitude, transfer_function_amplitude_color)
    plt.xticks(x_ticks_range)
    plt.yticks(amplitude_y_ticks_range)
    plt.grid()

    plt.subplot(2, 1, 2)
    plt.title('phase')
    plt.loglog(frequency, phase, transfer_function_phase_color)
    plt.xticks(x_ticks_range)
    plt.yticks(phase_y_ticks_range)
    plt.grid()

#-------------------------------------------------------------------------------
# Zeros
#
(zeroes, poles, gain) = sig.tf2zpk(FIR_coefficients, [1])
#print(zeroes)
                                                       # plot location of zeroes

if plot_zeros :
    max_amplitude = 1.1 * max(abs(zeroes))
    cutoff_angle = cutoff_frequency/sampling_rate*2*math.pi
    cutoff_x = max_amplitude * math.cos(cutoff_angle)
    cutoff_y = max_amplitude * math.sin(cutoff_angle)
    plt.figure("Zeros", figsize=(9, 9))
    plt.plot([-max_amplitude, max_amplitude], [0, 0], locus_axes_color)
    plt.plot([0, 0], [-max_amplitude, max_amplitude], locus_axes_color)
    plt.scatter(
        np.real(zeroes), np.imag(zeroes),
        marker='o', c=locus_zeroes_color)
    plt.plot(
        [cutoff_x, 0, cutoff_x], [-cutoff_y, 0, cutoff_y],
        locus_cutoff_frequency_color, linestyle='dashed'
    )
    plt.axis('square')

#-------------------------------------------------------------------------------
# Show plots
#
plt.show()