IIR 滤波器 通常基于连续时间滤波器函数 来设计。一旦选择了传递函数,不同的滤波器结构允许实现滤波器,无论是在硬件中还是在软件中。
经典的设计技术是从一个众所周知的低通滤波器函数 开始,然后将其变换 为高通、带通或带阻函数(如果需要)。经典的传递函数是
传递函数 的一般形式由两个多项式的比率给出

最直接的数字滤波器实现将通过实现其差分方程来完成,该方程由
![{\displaystyle y\left[k\right]=b_{0}x[k]+b_{1}x[k-1]+\cdots +b_{M}x[k-M]-a_{1}y[k-1]-a_{2}y[k-2]-\cdots -a_{N}y[k-N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fda4160d2142f0dbf6c2d8167c1b7c619daa7159)
以下电路显示了 4 阶滤波器差分方程的一种可能的实现方式
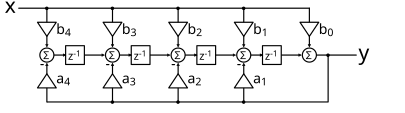 4 阶典范 IIR 滤波器
4 阶典范 IIR 滤波器
然而,这种形式在实践中并不使用。事实上,第一个尝试以这种方式实现滤波器的人发现该电路对系数值非常敏感:一个系数的微小变化可能会对滤波器传递函数的形状产生巨大影响。因此,将系数舍入为整数或定点 值会导致设计噩梦。正因为如此,工程师转向以下方法之一
- 模拟已被证明不会遭受这种严重敏感性的模拟滤波器结构
- 将总传递函数分解为二阶段链,对于偶数阶滤波器,再增加一个一阶段
全极点滤波器 限于低通器件。它们没有零点这一事实使其结构变得更加简单。事实上,它们的传递函数写成

一些基于模拟滤波器模拟的滤波器结构用于实现全极点滤波器。
巴特沃斯 和切比雪夫 I 型 函数都是全极点类型的。
带有反馈的积分器链 (CIF) 允许对全极点传递函数进行直接实现。
 四阶积分器链全极点滤波器
四阶积分器链全极点滤波器
此电路,其中  到
到  是乘法器输出,可以用以下方程描述
是乘法器输出,可以用以下方程描述

这可以通过迭代求解来得到






从这个式子中,可以从传递函数的系数中迭代地获取时间常数。
与模拟 CIF 相对应的数字结构在下图中给出
 模拟积分器链的 4 阶数字滤波器
模拟积分器链的 4 阶数字滤波器
如果采样率远高于时间常数,则可以从模拟域的 CIF 直接获取滤波器系数。否则,可以从采样系统传递函数中找到它们

其中  .
.
跳蛙滤波器 模拟 模拟梯形滤波器 的功能,并提供了全极点传递函数的稳健实现。可以证明,系数值的很大变化只会导致传递函数的小变化,特别是在通带内。
以以下 4 阶全极点低通梯形滤波器为例,
 4 阶集中元件梯形滤波器
4 阶集中元件梯形滤波器
可以写出以下方程

为了使左侧只有电压,重新编写这些方程

这组新方程表明,该滤波器可以使用 4 个积分器链来实现,积分器具有以下形式的
- 状态变量
 或
或 
- 时间常数 具有以下形式的
 或
或 
由此产生的电路是一个积分器链,其中每个积分器的输出都回馈到前一个积分器的输入。因此得名 leapfrog。

这种模拟设备可以通过用累加器替换模拟积分器来实现数字电路。

滤波器系数可以从表格中得出,表格提供  、
、 和
和  为所选的 滤波器函数 和采样周期
为所选的 滤波器函数 和采样周期  的值。一个有趣的点是系数的相对值决定了传递函数的形状 (巴特沃斯、切比雪夫 等),而它们的幅度决定了截止频率。将所有系数除以 2 会使截止频率降低一个倍频程,这对应于 2 的因子。
的值。一个有趣的点是系数的相对值决定了传递函数的形状 (巴特沃斯、切比雪夫 等),而它们的幅度决定了截止频率。将所有系数除以 2 会使截止频率降低一个倍频程,这对应于 2 的因子。
需要注意的是,用累加器替换模拟积分器是一种非常原始的设计技术。在信号处理方面,这对应于将 Z 变换简化为  ,这是 泰勒级数 的前两项
,这是 泰勒级数 的前两项  。然而,对于采样频率远高于信号带宽的滤波器,这种近似已经足够好。
。然而,对于采样频率远高于信号带宽的滤波器,这种近似已经足够好。
上述滤波器的 状态空间表示 可以写成

从这个方程组中,我们可以写出 A、B、C、D 矩阵为




有了这种表示,信号处理工具,例如 SciPy、Octave 或 Matlab,就可以绘制滤波器的 频率响应 或检查其 零点和极点。
一个特例是 巴特沃斯 3 级滤波器,其时间常数具有 1、1/2 和 1 的相对值。因此,这种滤波器可以在硬件中实现,无需任何乘法器,而是使用移位运算。
带有极点和零点的滤波器最适合以双二次单元链的形式实现,或者通过两个全通滤波器的并联连接实现。
二阶段,通常称为双二次,实现了一个二阶传递函数。滤波器的传递函数可以拆分成一系列传递函数的乘积,每个传递函数都与一对极点和可能的一对零点相关联。如果传递函数的阶数是奇数,则必须在链中添加一个一阶段。此部分与实极点和实零点(如果有)相关联。
二阶段的传递函数由下式给出

下面显示了最常见的双二次结构。
下图显示了直接形式 1 双二次
 直接形式 1 双二次
直接形式 1 双二次
下图显示了直接形式 1 转置双二次
 直接形式 1 转置双二次
直接形式 1 转置双二次
下图显示了直接形式 2 双二次
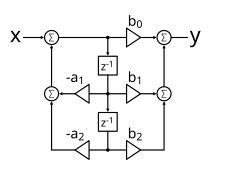 直接形式 2 双二次
直接形式 2 双二次
下图显示了直接形式 2 转置双二次
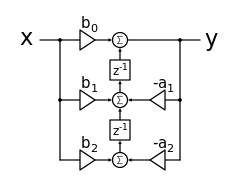 直接形式 2 转置双二次
直接形式 2 转置双二次
显然,相应的一阶段是通过去除系数  和
和  的乘法器以及相关的延迟元件来实现的。
的乘法器以及相关的延迟元件来实现的。
全通滤波器 用于修改信号频率分量的相位,而不改变其幅度。它们可用于补偿其他不需要的相移,例如在设计接近线性相位的 IIR 滤波器时。
此外,两个全通滤波器的并联连接允许实现任何类型的传递函数。事实上,在两个分支显示相同相移的频率处,输出将跟随输入,但在相对相移为 180° 的频率处,输出将为零。此功能的一个例子是在数字波滤波器 (WDFs) 系列中给出的。











![{\displaystyle y\left[k\right]=b_{0}x[k]+b_{1}x[k-1]+\cdots +b_{M}x[k-M]-a_{1}y[k-1]-a_{2}y[k-2]-\cdots -a_{N}y[k-N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fda4160d2142f0dbf6c2d8167c1b7c619daa7159)
































