离散数学/函数与关系

简介

本文考察了函数和关系的概念。

关系 是一个集合元素之间的任何关联或联系，这个集合被称为定义域（非正式地称为输入集），另一个集合被称为值域（或输出集）。有些人错误地将值域称为陪域，但正如我们将看到的，它实际上是指所有可能的输出，即使是关系实际上未使用的值。（注意：一些作者不使用陪域一词，而是使用值域来表示这个含义。这些作者使用像集 来表示我们称为值域的含义。因此，将值域或像集称为陪域是错误的，但将陪域称为值域并不一定是错误的。）

例如，如果定义域是集合 Fruits = {苹果，橙子，香蕉}，而陪域是集合 Flavors = {甜味，酸味，苦味}，那么这些水果的味道构成了一个关系：我们可以说苹果与两种味道（甜味和酸味）相关联，而橙子只与酸味相关联，香蕉只与甜味相关联。（我们可能略有不同意见，但这与本书主题无关。）注意，“苦味”虽然是 Flavors（陪域）中的一种可能味道，但实际上没有用于这些关系中的任何一个；因此它不是值域（或像集）{甜味，酸味}的一部分。

从另一个角度来看，我们可以说关系是有序对的子集，这些有序对从所有可能的有序对集合（两个其他集合的元素的有序对，我们通常称之为这些集合的笛卡尔积）中提取出来。形式上，R 是一个关系，如果

$R\subseteq X\times Y=\{(x,y)|x\in X,y\in Y\}$

对于定义域 X 和陪域 Y。R 的逆关系，写成 R^-1，是我们交换 X 和 Y 值时得到的结果

$R^{-1}=\{(y,x)|(x,y)\in R\}$

使用上面的例子，我们可以用集合符号写出关系：{(苹果，甜味)，(苹果，酸味)，(橙子，酸味)，(香蕉，甜味)}。逆关系，我们可以描述为“特定味道的水果”，是 {(甜味，苹果)，(甜味，香蕉)，(酸味，苹果)，(酸味，橙子)}。（这里，和其他地方一样，集合中元素的顺序没有意义。）

关系中一种重要的类型是函数。函数 是一种关系，对于定义域中的每个可能的输入，它都只有一个输出。（定义域不一定必须包含所有可能的给定类型的对象。事实上，我们有时有意使用受限定义域，以满足一些期望的性质。）上面讨论的关系（水果的味道和特定味道的水果）不是函数：第一个对于输入“苹果”有两个可能的输出（甜味和酸味）；第二个对于“甜味”（苹果和香蕉）和“酸味”（苹果和橙子）都有两个输出。

不允许对于同一个输入有多个输出的主要原因是，它让我们可以将同一个函数应用于同一个东西的不同形式，而不会改变它们的等价性。也就是说，如果 f 是一个在它的定义域中包含 a（或 b）的函数，那么 a = b 意味着 f(a) = f(b)。例如，z - 3 = 5 意味着 z = 8，因为 f(x) = x + 3 是一个对所有数字 x 定义明确的函数。

反之，f(a) = f(b) 意味着 a = b，并不总是成立。当它成立时，对于某个特定输出 y = f(x)，永远不会存在超过一个输入 x。这与函数的定义相同，但交换了 X 和 Y 的角色；因此这意味着逆关系 f^-1 也必须是一个函数。一般来说，无论原始关系是否是一个函数，逆关系有时是一个函数，有时不是。

当 f 和 f^-1 都是函数时，它们被称为一对一、单射或可逆函数。这是函数 f 可能（或可能不）拥有的两个非常重要的性质之一；另一个性质被称为满射或映射，这意味着，对于任何 y ∈ Y（在陪域中），都存在某个 x ∈ X（在定义域中），使得 f(x) = y。换句话说，一个满射函数 f 将映射到每个可能的输出至少一次。

一个函数可以是既不是一对一也不是满射，既是一对一又是满射（在这种情况下它也被称为双射或一一对应），或者仅仅是其中一个，而另一个不是。（作为既不是一对一也不是满射的例子，考虑 f = {(0,2)，(1,2)}。它是一个函数，因为它对于每个 x 值只有一个 y 值；但是对于输出 y = 2，存在多个输入 x；并且它显然没有“映射到”所有整数。）

关系

在上面关于函数及其性质的部分，我们注意到所有函数都必须具有的重要性质，即如果一个函数将值从其定义域映射到其陪域，它必须将该值映射到陪域中的唯一值。

用集合符号写出来，如果a 是某个固定值

|{f(x)|x=a}| ∈ {0, 1}

这个语句的字面意思是：对于某个固定值 a，集合 {f(x)|x=a} 的基数（元素数量）是集合 {0, 1} 的一个元素。换句话说，函数 f 在任何固定输入 a 处可能具有的输出数量要么为零（在这种情况下，它在该输入处未定义），要么为一（在这种情况下，输出是唯一的）。

然而，当我们考虑关系时，我们放宽了这种限制，因此一个关系可以将一个值映射到多个其他值。一般来说，关系是其定义域和陪域的笛卡尔积的任何子集。

那么，所有函数都可以被认为是关系。

符号

当一个值与另一个值相关联时，我们称这种关系为二元关系，我们将其写为

x R y

其中 R 是关系。

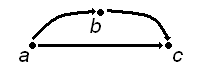
对于箭头图和集合符号，请记住，对于关系，我们没有函数的限制，我们可以画一个箭头来表示映射，对于集合图，我们只需要写下关系所采用的所有有序对：同样，举个例子

f = {(0,0),(1,1),(-1,1),(2,2),(-2,2)}

是一个关系而不是函数，因为 1 和 2 都映射到两个值（分别为 1 和 -1 以及 2 和 -2）例如，设 A=2,3,5；B=4,6,9 则 A*B=(2,4),(2,6),(2,9),(3,4),(3,6),(3,9),(5,4),(5,6),(5,9) 定义关系 R=(2,4),(2,6),(3,6),(3,9) 将函数和问题添加到彼此。

一些简单的例子

让我们考察一些简单的关系。

假设 f 由以下定义

{(0,0),(1,1),(2,2),(3,3),(1,2),(2,3),(3,1),(2,1),(3,2),(1,3)}

这是一个关系（而不是函数），因为我们可以观察到 1 映射到 2 和 3，例如。

小于，“<”，也是一种关系。许多数字可以小于某个固定的数字，因此它不能是函数。

属性

当我们查看关系时，我们可以观察到不同的关系可能具有一些特殊的属性。

自反

如果我们观察到对所有值 a

a R a

换句话说，所有值都与其自身相关联。

相等关系，“=” 是自反的。观察到，例如，对于所有数字 a（域为 R）

a = a

所以“=” 是自反的。

在自反关系中，我们有所有域中值的箭头指向自身

请注意，≤ 也是自反的（a ≤ a 对于 R 中的任何 a 成立）。另一方面，关系 < 不是（a < a 对于 R 中的任何 a 都是假的）。

对称

如果我们观察到对所有值 a 和 b

a R b 意味着 b R a

相等关系再次是对称的。如果 x=y，我们也可以写成 y=x。

在对称关系中，对于每个箭头，我们也都有一个相反的箭头，即 x 和 y 之间要么没有箭头，要么箭头从 x 指向 y，然后箭头从 y 指向 x

≤ 和 < 都不是对称的（2 ≤ 3 和 2 < 3 但 3 ≤ 2 和 3 < 2 都不成立）。

传递

如果对所有值 a、b、c

a R b 和 b R c 意味着 a R c

关系大于“>” 是传递的。如果 x > y 且 y > z，则 x > z 成立。当我们将发生的事情写成文字时，这变得更加清楚。x 大于 y 且 y 大于 z。所以 x 大于 y 和 z。

关系不等于“≠” 不是传递的。如果 x ≠ y 且 y ≠ z，那么我们可能会有 x = z 或 x ≠ z（例如 1 ≠ 2 且 2 ≠ 3 且 1 ≠ 3 但 0 ≠ 1 且 1 ≠ 0 且 0 = 0）。

在箭头图中，两个值 a 和 b 之间，以及 b 和 c 之间的每个箭头都有一个箭头直接从 a 指向 c。

反对称

如果我们观察到对所有值 a 和 b

a R b 和 b R a 意味着 a=b

请注意，反对称与“非对称”不同。

取关系大于或等于，“≥” 如果 x ≥ y 且 y ≥ x，则 y 必须等于 x。当且仅当 a∈A，(a,a)∈R 时，关系是反对称的

三等分

如果我们观察到对所有值 a 和 b，它都成立：aRb 或 bRa，则关系满足三等分。

关系大于或等于满足，因为对于给定的 2 个实数 a 和 b，a ≥ b 或 b ≥ a 成立（如果 a = b，则两者都成立）。

问题集

鉴于以上信息，确定哪些关系在以下方面是自反的、传递的、对称的或反对称的 - 可能存在多个特征。（答案如下。）x R y 如果

1. x = y
2. x < y
3. x² = y²
4. x ≤ y

答案

1. 对称、自反和传递
2. 传递、三等分
3. 对称、自反和传递（x² = y² 只是相等的一个特例，所以适用于 x = y 的所有属性也适用于这种情况）
4. 自反、传递和反对称（并满足三等分）

等价关系

我们已经看到，某些常见的关系，如“=” 和全等（我们将在下一节中讨论）遵守上述某些规则。我们将讨论的关系在离散数学中非常重要，被称为等价关系。它们本质上断言某种相等概念或等价性，因此得名。

等价关系的特征

对于关系 R 成为等价关系，它必须具有以下属性，即 R 必须是

• 对称的
• 传递的
• 自反的

（一个有用的助记符，S-T-R）

在前面的问题集中，您已经证明了相等，“=”，是自反的、对称的和传递的。所以“=” 是等价关系。

一般情况下，我们用 $x\sim y$ 来表示等价关系。

示例证明

假设我们被要求证明“=” 是等价关系。然后，我们依次证明上面的每个属性（通常，传递性的证明是最难的）。

• 自反：显然，a = a 对所有值 a 成立。因此，= 是自反的。
• 对称：如果 a = b，则 b = a 也成立。因此，= 是对称的
• 传递性：如果a = b 且 b = c，这意味着a 与b 相同，而b 又与c 相同。所以a 也与c 相同，所以a = c，因此 = 是传递的。

因此 = 是一个等价关系。

划分和等价类

当我们处理关系时，我们会发现很多值与一个固定值相关联，这是真的。

例如，当我们查看同余的性质时，该性质是指对于给定的一些数字a，与a 同余的数字是那些在被某个数字n 除后具有相同余数或模数的数字，与a 相同，我们写成

a ≡ b (mod n)

这与写成以下形式相同

b = a+kn，其中 k 是某个整数。

（我们将在后面详细介绍同余，但对这一概念的简单考察或理解将在其对等价关系的应用中很有趣）

例如，2 ≡ 0 (mod 2)，因为 2 除以 2 的余数实际上是 0，0 除以 2 的余数也是 0。

我们可以证明同余是一个等价关系（这留作练习，在下面的提示中使用上面描述的同余的等价形式）。

然而，更有趣的是我们可以将所有彼此等价的数字分组。

对于模 2 同余关系（即使用 n=2，如上），或者更正式地说

x ~ y 当且仅当 x ≡ y (mod 2)

我们可以将所有彼此等价的数字分组。观察

$0\equiv 2\equiv 4\equiv \ldots {\pmod {2}}$

$1\equiv 3\equiv 5\equiv \ldots {\pmod {2}}$

上面的第一个方程式告诉我们所有偶数在 ~ 下彼此等价，所有奇数在 ~ 下彼此等价。

我们可以用集合符号来表示。然而，我们有一个特殊的符号。我们写

[0]={0,2,4,...}

[1]={1,3,5,...}

我们称这两个集合为等价类。

根据定义，等价类中的所有元素彼此等价，因此请注意，我们不需要包含 [2]，因为 2 ~ 0。

我们将根据某个等价关系执行此“分组”的行为称为划分（或者更进一步地明确地根据关系 ~ 将集合 S 划分成等价类）。在上面，我们根据模 2 同余关系将Z 划分成了等价类 [0] 和 [1]。

问题集

鉴于上述内容，请回答以下有关等价关系的问题（答案在偶数编号的问题后面给出）

1. 证明同余如前所述是一个等价关系（见上面的提示）。
2. 将 {x | 1 ≤ x ≤ 9} 划分成等价关系下的等价类

$x\sim y\ {\mbox{iff}}\ x\equiv y{\pmod {6}}$

答案

2. [0]={6}, [1]={1,7}, [2]={2,8}, [3]={3,9}, [4]={4}, [5]={5}

偏序

我们还看到“≥”和“≤”服从上面的一些规则。这些也是特殊类型的关系吗，就像等价关系一样？是的，事实上，这些关系是我们将在此部分中描述的另一种特殊类型关系的具体例子：偏序。

顾名思义，这种关系对数字进行某种排序。

偏序的特征

为了使关系 R 成为偏序，它必须具有以下三个属性，即 R 必须是

• 自反的
• 反对称的
• 传递的

（一个有用的助记符，R-A-T）

我们一般用 $x\preceq y$ 表示偏序。

问题

1. 假设 R 是整数集 Z 上的关系，那么证明 R 是 Z 上的偏序关系当且仅当 a=b 的 r 次方。

示例证明

假设我们要证明“≤”是一个偏序。然后我们依次证明上面的每个属性（通常，传递性的证明是最难的）。

自反

显然，对于所有值 a，a ≤ a 都是成立的。所以 ≤ 是自反的。

反对称

如果a ≤ b 且 b ≤ a，那么a 必须等于b。所以 ≤ 是反对称的

传递

如果a ≤ b 且 b ≤ c，这意味着a 小于b 和c。所以a 小于c，所以a ≤ c，因此 ≤ 是传递的。

因此 ≤ 是一个偏序。

问题集

鉴于上述关于偏序的内容，请回答以下问题

1. 证明可除性 | 是一个偏序（a | b 表示 a 是 b 的因子，即在用 a 除 b 时，没有余数）。
2. 证明以下集合是一个偏序：（a, b) $\preceq$ (c, d) 意味着 ab≤cd，其中 a,b,c,d 是从 0 到 5 的整数。

答案

2. 简单的证明；证明的形式化是一个可选练习。

自反性：（a, b) $\preceq$ (a, b)，因为 ab=ab。

反对称性： (a, b) $\preceq$ (c, d) 且 (c, d) $\preceq$ (a, b) ，因为 ab≤cd 且 cd≤ab 意味着 ab=cd。

传递性： (a, b) $\preceq$ (c, d) 且 (c, d) $\preceq$ (e, f) 意味着 (a, b) $\preceq$ (e, f) ，因为 ab≤cd≤ef ，因此 ab≤ef

偏序集

偏序关系赋予了集合中元素某种“顺序”。例如，我们只知道 2 ≥ 1，这是因为偏序关系 ≥。

我们称在一个一般偏序关系 $\preceq$ 下有序的集合 A 为一个偏序集，简称为poset，并将其记为 (A, $\preceq$).

术语

一些特定的术语将有助于我们理解和可视化偏序关系。

当我们有一个偏序关系 $\preceq$，使得 a $\preceq$ b，我们写 $\prec$ 来表示 a $\preceq$ 但 a ≠ b。在这种情况下，我们说 a先于b，或者a是b的前驱。

如果 (A, $\preceq$) 是一个 poset，我们说 a 是 b 的直接前驱（或 a 直接先于 b），如果 A 中不存在 x 使得 a $\prec$ x $\prec$ b。

如果我们有相同的 poset，并且 A 中也存在 a 和 b，那么如果 a $\preceq$ b 或 b $\preceq$ a，我们说 a 和 b 是可比较的。否则，它们是不可比较的。

哈斯图

哈斯图是特殊的图，使我们能够可视化偏序关系的结构。它们使用上一节中的一些概念来绘制图。

poset (A, $\preceq$) 的哈斯图的构造方法是

• 将 A 的元素作为点放置
• 如果 a 和 b ∈ A，且 a 是 b 的直接前驱，则从 a 到 b 画一条线
• 如果 a $\prec$ b，将 a 的点放在 b 的点下方
• 不从 a 到 a 画环路（由于自反性，这在偏序关系中是假设的）

关系上的运算

在关系上可以执行一些有用的运算，这些运算可以更简洁地表达上面提到的某些性质。

反转

设 R 为一个关系，则其反转 R^-1 定义为

R^-1 := {(a,b) | (b,a) in R}.

连接

设 R 是集合 A 和 B 之间的关系，S 是集合 B 和 C 之间的关系。我们可以通过定义以下方式连接这些关系：

R • S := {(a,c) | (a,b) ∈ R 且 (b,c) ∈ S，对于 B 中的某个 b}

集合的对角线

设 A 是一个集合，我们定义 A 的对角线 (D) 为：

D(A) := {(a,a) | a ∈ A}

简短的记号

使用上面的定义，我们可以说（假设 R 是 A 和 B 之间的关系）：

R 是传递的当且仅当 R • R 是 R 的子集。

R 是自反的当且仅当 D(A) 是 R 的子集。

R 是对称的当且仅当 R^-1 是 R 的子集。

R 是反对称的当且仅当 R 和 R^-1 的交集是 D(A)。

R 是非对称的当且仅当 D(A) 和 R 的交集为空。

R 是一个函数当且仅当 R^-1 • R 是 D(B) 的子集。

在这种情况下，它是一个 A → B 的函数。假设 R 满足函数的条件，那么：

R 是单射的当且仅当 R • R^-1 是 D(A) 的子集。

R 是满射的当且仅当 {b | (a,b) ∈ R} = B。

函数

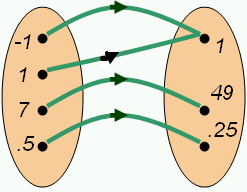
函数是两个数字集合之间的关系。我们可以将其视为一种映射；函数将一个集合中的一个数字映射到另一个集合中的一个数字。请注意，函数将值映射到一个且只有一个值。一个集合中的两个值可以映射到一个值，但一个值永远不能映射到两个值：这将是一个关系，而不是一个函数。

例如，如果我们将一个函数定义为：

$f(x)=x^{2}$

那么我们说：

'f of x 等于 x 的平方'

我们有：

$f(-1)=1$

$f(1)=1$

$f(7)=49$

$f(1/2)=1/4$

$f(4)=16$

等等。

这个函数 f 将数字映射到它们的平方。

值域和陪域

如果 D 是一个集合，我们可以说：

$f(D)=\{f(x)|\ x\in D\}$

这形成了 f 的值域，通常是更大集合的子集。这个集合被称为函数的陪域。例如，对于函数 f(x)=cos x，f 的值域是 [-1,1]，但陪域是实数集合。

符号

当我们有一个函数 f，其定义域为 D，值域为 R 时，我们写：

$f:D\longrightarrow R$

如果我们说，例如，x 映射到 x²，我们也可以添加：

$f:D\longrightarrow R;\ x\longmapsto x^{2}$

请注意，我们可以有一个函数将点 (x,y) 映射到一个实数，或者其他一些两个变量的函数 - 我们有一组有序对作为定义域。回想一下集合论，这是由笛卡尔积定义的 - 如果我们想表示所有实值有序对的集合，我们可以将实数与它自身进行笛卡尔积，以得到：

$\mathbb {R} \times \mathbb {R} =\mathbb {R} ^{2}=\{(x,y)|\ x\ {\mbox{and}}\ y\in \mathbb {R} \}$.

当我们有一个由n元组组成的集合作为域时，我们就说这个函数是n元的（对于数字n=1,2，我们分别称为一元和二元）。

其他函数表示法

函数可以用上面提到的方式写，但我们也可以用两种其他方式写。一种方式是使用箭头图来表示每个元素之间的映射关系。我们把域中的元素写在一侧，把值域中的元素写到另一侧，然后画箭头表示域中的元素映射到值域中的元素。

例如，对于函数f(x)=x³，域为{1,2,3}的箭头图将是：

另一种方法是使用集合符号。如果f(x)=y，我们可以用映射关系来表示函数。这个概念最好用例子来解释。

让我们取域D={1,2,3}，并且f(x)=x²。那么，f的值域将是R={f(1),f(2),f(3)}={1,4,9}。对D和R取笛卡尔积，我们得到F={(1,1),(2,4),(3,9)}。

因此，使用集合符号，函数可以表示为其域和值域的笛卡尔积。

f(x)

这个函数被称为f，它接受一个变量x。我们用某个值替换x，得到第二个值，也就是函数将x映射到的值。

函数的类型

函数可以是一对一（单射）、映上（满射）或双射。

单射函数是指域中的每个元素都映射到陪域中唯一的元素的函数。

满射函数是指陪域中的每个元素都被域中的某个元素映射的函数。

'双射 函数是指既是单射又是满射的函数。

---满射函数 从A到B的函数f是满射的，