离散数学/集合论/第 2 页

幂集

一个集合 A 的幂集 是所有子集的集合（包括它本身和空集）。它表示为 P(A)。

使用集合推导符号，P(A) 可以定义为

P(A) = { Q | Q ⊆ A }

示例 4

如果 A 是

(a) A = {1, 2, 3}

(b) A = {1, 2}

(c) A = {1}

(d) A =ø

解

(a) P(A) = { {1, 2, 3}, {2, 3}, {1, 3}, {1, 2}, {1}, {2}, {3},ø }

(b) P(A) = { {1, 2}, {1}, {2},ø }

(c) P(A) = { {1},ø }

(d) P(A) = {ø }

幂集的基数

看看示例 4 中四个集合的基数，以及它们相应幂集的基数。它们是

	| A |	| P(A) |
(a)	3	8
(b)	2	4
(c)	1	2
(d)	0	1

很明显，这里有一个简单的规律在起作用：用 2 的幂表示，幂集的基数分别是 2³、2²、2¹ 和 2⁰。

看起来我们发现了一个规律，如果 | A | = k，那么 | P(A) | = 2^k。但我们能看出原因吗？

好吧，A 的幂集的元素是 A 的所有可能的子集。任何一个这样的子集都可以通过以下方式形成

• 选择 A 的任何一个元素。我们可以决定将它包含在我们的子集中，也可以省略它。因此，处理 A 的第一个元素有 2 种方法。

• 现在选择 A 的第二个元素。和以前一样，我们可以将它包含在我们的子集中，也可以从我们的子集中省略它：同样是处理该元素的 2 种方法。

• ...就这样一直处理 A 的所有 k 个元素。

现在，组合学的基准原理告诉我们，如果我们能以 2 种方式完成 k 件事情中的每一件，那么依次完成所有事情的总方法数为 2^k。

这些 2^k 种决策组合中的每一种——包含元素或省略元素——都会给我们 A 的一个不同的子集。因此，总共有 2^k 个不同的子集。

所以，如果 | A | = k，那么 | P(A) | = 2^k。

集合论的基本规则

下面列出的定律 可以被称为集合论的基本规则。我们通过回到交集、并集、全集和空集的定义，并考虑给定元素是否在一个或多个集合中，来推导出这些定律。

幂等律

例如，我们将考虑“我第一次听到你”定律——更准确地说，被称为幂等律——它们指出

A ∩ A = A 并且 A ∪ A = A

如果你学习过逻辑，你可能对这条定律很熟悉。上述关系类似于重言式。

这些看起来很明显，对吧？对这些定律的交集部分的一个简单的解释是这样的

两个集合 A 和 B 的交集定义为仅包含在 A 中且在 B 中的元素。如果我们在该定义中用 A 代替 B，我们得到 A 和 A 的交集是包含仅在 A 中且在 A 中的元素的集合。显然，我们不需要重复说两次（我第一次听到你），所以我们可以简单地说 A 和 A 的交集是 A 中的元素的集合。换句话说

A ∩ A = A

我们可以用类似的方式推导出 A ∪ A = A 的解释。

德摩根定律

有两条定律，被称为德摩根定律，告诉我们如何去掉括号，当括号外面有一个补符号——′——时。其中一条定律是这样的

(A ∪ B) ′ = A ′ ∩ B ′

（如果你已经完成了练习 3，第 4 题，你可能已经从文氏图中发现了这条定律。）

仔细看看这条定律是如何工作的。括号后的补符号在括号被移除时会影响括号内的所有三个符号

A 变为 A ′

B 变为 B ′

而 ∪ 变为 ∩。

为了证明这条定律，首先注意到，当我们定义子集时，我们说如果

A ⊆ B 并且 B ⊆ A，那么 A = B

所以我们证明

(i) (A ∪ B) ′ ⊆ A ′ ∩ B ′

然后反过来

(ii) A ′ ∩ B ′ ⊆ (A ∪ B) ′

(i) 的证明是这样的

让我们随机选取一个元素 x ∈ (A ∪ B) ′。我们对 x 一无所知；它可以是一个数字，一个函数，甚至是一头大象。我们对 x 所知道的只是

x ∈ (A ∪ B) ′

所以

x ∉ (A ∪ B)

因为这就是补的含义。

这意味着 x 对你在 A 中吗？和你在 B 中吗？这两个问题都回答否（否则它将在 A 和 B 的并集中）。因此

x ∉ A 并且 x ∉ B

再次使用补运算，我们得到

x ∈ A ′ 并且 x ∈ B ′

最后，如果一个东西在两个集合中，它一定在它们的交集中，所以

x ∈ A ′ ∩ B ′

所以，我们从 (A ∪ B) ′ 中随机选取的任何一个元素肯定都在 A ′ ∩ B ′ 中。因此，根据定义

(A ∪ B) ′ ⊆ A ′ ∩ B ′

(ii) 的证明类似

首先，我们从第一个集合中随机选取一个元素，x ∈ A ′ ∩ B ′

使用我们对交集的了解，这意味着

x ∈ A ′ 并且 x ∈ B ′

所以，使用我们对补运算的了解，

x ∉ A 并且 x ∉ B

如果一个东西既不在 A 中也不在 B 中，它就不能在它们的并集中，所以

x ∉ A ∪ B

所以，最后

x ∈ (A ∪ B) ′

所以

A ′ ∩ B ′ ⊆ (A ∪ B) ′

我们现在已经证明了 (i) 和 (ii)，因此

(A ∪ B) ′ = A ′ ∩ B ′

这让你体验了这些定律背后的内容。所以，这里列出了所有定律。

集合定律

交换律

A ∩ B = B ∩ A

A ∪ B = B ∪ A

结合律

(A ∩ B) ∩ C = A ∩ (B ∩ C)

(A ∪ B) ∪ C = A ∪ (B ∪ C)

分配律

A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

幂等律

A ∩ A = A

A ∪ A = A

恒等律

A ∪ø= A

A ∩ U = A

A ∪ U = U

A ∩ø = ø

对合律 (A ′) ′ = A

补律

A ∪ A' = U

A ∩ A' =ø

U ′ =ø

ø′ = U

德摩根定律

(A ∩ B) ′ = A ′ ∪ B ′

(A ∪ B) ′ = A ′ ∩ B ′

对偶性与布尔代数

您可能注意到以上集合定律成对出现：如果在任何给定的定律中，您将∪替换为∩，反之亦然（并且，如果需要，交换U和ø)，您将得到另一条定律。每对中的“伙伴定律”被称为对偶，每条定律都是另一条定律的对偶。

• 例如，德摩根定律中的每一项都是另一项的对偶。

• 第一个补律，A ∪ A ′ = U，是第二个的对偶：A ∩ A ′ =ø.

• 等等。

这被称为对偶原理。实际上，这意味着您只需要记住这张表格的一半！

这组定律构成了布尔代数的公理。更多信息请参见 布尔代数。

使用集合定律的证明

我们可以使用这些定律 - 并且只有这些定律 - 来确定关于集合之间关系的其他陈述是真还是假。韦恩图可能有助于暗示这些关系，但只有基于这些定律的证明才会被数学家认为是严谨的。

示例 5

使用集合定律，证明集合 (A ∪ B) ∩ (A ′ ∩ B) ′ 实际上与集合A相同。仔细说明您在每个阶段使用的定律。

在开始证明之前，先说几个“做”和“不要”

做从单个表达式 (A ∪ B) ∩ (A ′ ∩ B) ′ 开始，目标是将其简单地更改为A。	不要从写下整个等式 (A ∪ B) ∩ (A ′ ∩ B) ′ = A 开始 - 这就是我们必须得到的最终结果。
做一次只改变表达式的其中一部分，一次只使用一个集合定律。	不要省略步骤，一次改变两件事。
做将等号彼此对齐。	不要让您的工作变得杂乱无章且布局混乱。
做说明您在每个阶段使用的定律。	不要认为即使是最简单的步骤也是理所当然的。

解

		使用的定律
(A ∪ B) ∩ (A ′ ∩ B) ′	= (A ∪ B) ∩ ((A ′) ′ ∪ B ′)	德摩根定律
	= (A ∪ B) ∩ (A ∪ B ′)	对合律
	= A ∪ (B ∩ B ′)	分配律
	= A ∪ø	补律
	= A	恒等律

我们现在已经证明了 (A ∪ B) ∩ (A ′ ∩ B) ′ = A，无论集合A和B包含什么。像这样的陈述 - 对A和B的所有值都为真的陈述 - 有时被称为恒等式。

证明提示

这些证明没有万无一失的方法 - 练习是最好的指导。但这里有一些一般性提示。

• 从等式中更复杂的一侧开始，目标是将其简化为另一侧。

• 寻找分配律会导致简化的位置（就像“普通”代数中的因式分解 - 请参阅上面的示例 5中的第三行）。

• 您可能需要使用德摩根定律来摆脱括号外的“符号”。

• 有时您可能需要“复杂化”一个表达式，然后才能对其进行简化，正如下一个示例所示。

示例 6

使用集合定律证明A ∪ (A ∩ B) = A。

看起来很容易，是吗？但是你可能会在这个问题上走很多弯路。（如果你喜欢，先尝试一下，然后再阅读下面的解决方案。）关键是首先“复杂化”它，将第一个A 写成A ∩ U（使用恒等律之一）。

解

		使用的定律
A ∪ (A ∩ B)	= (A ∩ U) ∪ (A ∩ B)	恒等律
	= A ∩ (U ∪ B)	分配律
	= A ∩ (B ∪ U)	交换律
	= A ∩ U	恒等律
	= A	恒等律

集合论练习 4

点击链接查看 集合论练习 4。

笛卡尔积

有序对

为了介绍这个主题，我们首先来看几个使用我们之前提到的组合原理的例子（参见 基数）；即，如果事件R可以发生r种方式，而第二个事件S然后可以发生s种方式，那么事件R和S依次发生的总方式数为r × s。这有时被称为r-s 原理。

示例 7

菜单

主菜

清蒸比目鱼

烤羊肉

蔬菜咖喱

千层面

甜点

新鲜水果沙拉

苹果派

蛋糕

从上面的菜单中可以选出多少种不同的套餐 - 主菜加甜点？

解

由于我们可以用四种方式选择主菜，然后用三种方式选择甜点来形成每次不同的组合，因此，使用r-s 原理，答案是共有 4 × 3 = 12 种不同的套餐。

示例 8

您正在准备出门。您有 5 条不同的（干净的！）内裤和两条牛仔裤可供选择。您可以用多少种方式选择穿一条内裤和一条牛仔裤？

解

使用r-s 原理，有 5 × 2 = 10 种方式可以依次选择这两件衣服。

在以上两种情况下，我们都有有序对的例子。顾名思义，有序对仅仅是一对以特定顺序排列的“事物”。通常，选择事物顺序是任意的 - 我们只需要决定一种约定，然后坚持下去；有时顺序实际上只有一种方式。

就套餐而言，大多数人选择先吃主菜，然后吃甜点。在穿着的衣服中，我们在牛仔裤之前穿上内裤。您完全可以违背惯例，先吃甜点，然后吃主菜 - 或者将内衣穿在裤子上 - 但如果您这样做，您将得到不同的有序对集。当然，您通常需要解释很多！

组成有序对的两个“事物”用圆括号括起来，并用逗号隔开；就像这样

(千层面，蛋糕)

如果您做过坐标几何，那么您之前就遇到过有序对。例如，(2, 3) 表示x轴上向右移动 2 个单位，y轴上向上移动 3 个单位的点。在这里，在数字的顺序中也存在着一种约定：我们使用字母顺序，将x坐标放在y坐标之前。（同样，您可以选择以相反的方式进行坐标几何，将y放在x之前，但是，您需要解释很多！)

因此，使用集合符号，我们可以像这样描述示例 7中的情况

M = {主菜}，D = {甜点}，C = {完整的套餐}。

那么C可以写成

C = { (m, d) | m ∈ M 且 d ∈ D }。

C被称为集合积或笛卡尔积M和D，我们写成

C = M × D

(读作“C 等于 M 叉乘 D”)

假设示例 7中的菜单扩展到包括开胃菜，可以是汤或果汁。现在可以选出多少种完整的套餐？

好吧，我们可以扩展r-s 原理以包含第三个选择，并得到 2 × 4 × 3 = 24 种可能的套餐。

如果S = {汤，果汁}，那么我们可以写成

C = S × M × D

此集合的元素是有序三元组：(开胃菜，主菜，甜点)。因此，请注意，这些项目在三元组中出现的顺序与它们被选择的集合的顺序相同：S × M × D 没有给我们与 M × D × S 相同的有序三元组集。

有序n元组

一般来说，如果我们有n个集合：A₁, A₂, ..., A_n，那么它们的笛卡尔积定义为

A₁ × A₂ × ... × A_n = { (a₁, a₂, ..., a_n) | a₁ ∈ A₁, a₂ ∈ A₂, ..., a_n ∈ A_n) }

而 (a₁, a₂, ..., a_n) 被称为 有序n元组。

符号

A₁ × A₂ × ... × A_n 有时写成

$\times _{i=1}^{n}$ A_i

笛卡尔平面

笛卡尔平面：图8

你可能已经知道用有序对来表示平面上的一个点的方式。图8中的图表说明了一个笛卡尔平面，显示了用有序对(5, 2)表示的点。

这些线被称为轴：x轴和y轴。它们相交的点被称为原点。点(5, 2)的位置如下：从原点开始；沿着x轴方向移动5个单位，然后沿着y轴方向移动2个单位。

使用集合符号

如果X = {x轴上的数字} 且 Y = {y轴上的数字}，那么

(5, 2) ∈ X × Y

而且，事实上，如果X = {所有实数} 且 Y = {所有实数}，那么X × Y作为一个整体代表了x-y平面中的所有点。

(这就是你有时会看到x-y平面被称为R²的原因，其中R = {实数}。)
示例9

据信，如果A, B, P和Q是B ⊂ A 且 Q ⊂ P的集合，那么

B × Q ⊂ A × P

使用仔细阴影和标记的笛卡尔图来研究这个命题。

解

考虑到我们上面提到的X × Y中的有序对对应于x-y平面中的点，如果我们想在图中表示A × P这样的笛卡尔积，我们需要分别在x轴和y轴上将A和P表示为点集。

表示笛卡尔积A × P的区域是由x和y坐标位于这些集合A和P内的点表示。像这样

笛卡尔平面：图9a

对于B和Q也可以说同样的话：B必须位于x轴上，Q必须位于y轴上。

此外，由于B ⊂ A，因此我们必须将B表示为从A的元素中选择的集合。类似地，由于Q ⊂ P，Q的元素必须位于P的元素内。

当我们在图中添加这些组件时，它看起来像这样

笛卡尔平面：图9b

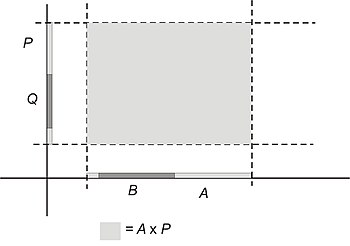
最后，当我们用一个矩形来表示集合B × Q，该矩形的限制由B和Q的限制决定，很明显，这个矩形将位于表示A × P的矩形内

笛卡尔平面：图9c

因此，命题B × Q ⊂ A × P似乎是正确的。

集合论习题5

点击链接以获取集合论习题5。