工程热力学/热力学系统
一般来说,系统是指一组物体,定义系统的方式很微妙,就像集合论一样。然而,在热力学中,它是一个更加直接的概念。
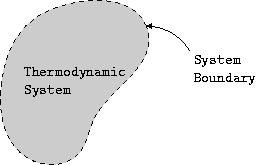
热力学**系统**是指占据一定体积并具有边界的空间区域或有限量。**环境**是指系统外部的任何事物。将系统与其环境隔开的虚线称为**边界**。边界定义了系统的范围。边界可以是固定的,也可以是移动的。系统及其环境一起构成了**宇宙**。
有时使用**控制体积**代替系统。在封闭系统的情况下,系统内部物质的质量保持不变,控制体积称为**控制质量**。控制体积被**控制面**包围。
接下来,通用术语系统将用于指代热力学系统。
孤立系统是不允许与环境交换质量或能量的系统。孤立系统根本不与其环境相互作用。系统的边界不允许质量或能量传递。
保温瓶是孤立系统的近似模型,它通过真空边界来减缓液体与外部空气之间的相互作用,从而保持液体的温度。唯一真正的孤立系统是宇宙。
封闭热力学系统是指允许与环境交换热量和功,但不允许任何质量跨越边界的系统。由于边界没有流动,因此这种类型的系统也称为非流动系统。带有气缸的往复式发动机的气缸和活塞是封闭系统的示例。另一个简单的例子是水壶,其中热量被供应到水壶,但其中包含的水量保持恒定。
开放热力学系统是指允许与环境交换质量和能量的系统。系统内部的质量会随时间变化。开放系统也称为控制体积。
空气压缩机是开放系统的示例,它从环境中吸入空气,将其压缩到高压,然后通过喷嘴从系统中释放。
绝热系统是指允许与环境交换功但不允许交换热的系统。系统通过热绝缘边界来实现这一点。
连续体是指包含连续物质分布的系统。连续体将系统中的物质视为均匀分布在空间中,并且不考虑单个原子或分子的作用。压力、温度和其他性质是许多原子和分子共同性质的平均值。
物质在其物理结构和化学组成上是均匀的,称为其相。最常见的相是固态、液态和气态。
均相系统仅由单一相组成。纯物质和均相混合物是均相系统的例子。
非均相系统由两种或多种不同相组成。
对性质的简单回顾将向学生介绍热力学的变量。物质的性质是指质量、温度、体积和压力等。性质用于定义物质的当前状态。热力学中存在几个其他性质来描述物质,但需要对理论有更深入的了解才能对其进行定义和应用。
性质可以是密集的,如果它们是点性质(对点有意义的性质)或广泛的,如果它们取决于系统中物质的数量。系统广泛性质的例子包括系统的质量、系统中物质的摩尔数以及系统的总体积或总积。这些性质取决于您测量系统的多少物质。密集性质的例子包括压力、温度、密度、每单位质量的体积、摩尔体积(即每摩尔的体积)以及平均分子量(或分子质量)。这些性质与您如何改变物质质量无关。
性质就像物质的变量,因为它们的值都通过一个方程相关联。性质之间的关系以方程的形式表达,称为状态方程。也许最著名的状态方程是理想气体定律。理想气体定律将理想气体的压力、体积和温度相互关联。
体积的 SI 单位为m3。
体积是一个广泛的性质,但每单位质量的体积和摩尔体积都是密集的性质,因为它们不依赖于系统测量的质量。体积保持恒定的过程称为等容(或等容)过程。
压力的 SI 单位为 Pa(帕斯卡),相当于。压力是一个密集的性质。压力保持恒定的过程称为等压过程。
温度,物体的冷热程度,被定义为。根据热力学第零定律,是热力学的基本概念。我们知道,温度高的物体将能量转移到温度低的物体。考虑两个温度不同的物体相互接触。净能量转移将从较热的物体转移到较冷的物体。在某一点,净能量转移将为零,并且物体被认为处于热平衡状态。处于热平衡状态的物体被定义为具有相同的温度。
经典热力学处理的是处于平衡状态的系统。平衡状态由系统中可观察量的值定义。这些被称为系统性质。
描述系统所需的最小变量数量取决于系统的复杂性或自由度。自由度是指在系统中可以相互独立改变的性质的数量。一些常见的系统变量是压力、温度和密度,尽管可以使用任何其他物理性质。
与学科发展的公理性质一致,许多物理性质之间的关系无法在没有进一步理论发展的情况下完全指定。经典热力学的好处是,这里陈述的许多公理可以使用统计热力学技术推导出。统计热力学在许多情况下给出了经典热力学无法给出结果的地方,例如在具有许多自由度的气体的比热中。在某种意义上,经典热力学与统计热力学之间的关系类似于经典力学与量子力学之间的关系,即,经典热力学在宏观极限情况下近似于统计热力学。
系统状态的变化称为过程。当过程的初始状态和最终状态相同时,该过程称为循环。如果一个过程可以反转运行而系统+环境没有发生变化,则该过程称为可逆过程。如果一个过程不可逆,则称为不可逆过程。
等温过程是指温度保持恒定的过程。请注意,一个过程是等温的并不意味着任何关于传递的热量或所做的功,即,在等温过程中可能会发生热量传递。等温过程意味着对于理想气体,体积和压力的乘积是恒定的。即 PV = 常数
如果系统A与另一个系统B以及第三个系统C处于热平衡状态,那么所有系统彼此都处于热平衡状态。这被称为热力学第零定律。这就是温度计的工作原理。如果将温度计放入物质中进行温度测量,温度计的玻璃会与物质达到热平衡。然后玻璃会与温度计内部的液体(汞、酒精等...)达到热平衡。因为物质与玻璃处于热平衡状态,而玻璃与内部液体处于热平衡状态,所以根据第零定律,物质和液体必须处于热平衡状态。并且因为它们热力学等效,所以它们必须具有相同的温度。
温度是通过观察系统随温度变化的某些性质来测量的。这样的性质称为测温性质,例如
- 大多数液体的体积随温度升高而增大。
- 金属棒的长度随温度升高而增大。
- 恒定体积气体的压力随温度升高而增大
建立一个温度刻度很有用,以便可以在不同温度下的各种系统之间建立基数关系。这是通过定义温度t作为测温性质X的函数来实现的,使得温度是X的线性函数,即,性质X的相等变化会导致温度的相等变化。这样的线性函数是t = a + b X,为此需要将任意温度分配给X的两个值以找到常数a和b的值。
例如,在摄氏刻度的情况下,测量基于水在沸点和熔点时的性质。假设测温性质的值对于正常沸点为Xb,对于正常熔点为Xm。则温度由t = 100 (X - Xm)/(Xb - Xm)给出,其中X是温度为t时的测温性质,我们选择了tm = 0 °C 和tb = 100 °C。正常熔点和沸点是在 1 个大气压压力下的熔点和沸点温度。
主要的温度刻度是摄氏 (°C)、华氏 (°F) 和开尔文 (K) 刻度。注意开尔文没有°符号——它不是开尔文度,而是开尔文,拼写时不使用大写字母,并使用英语的正常复数形式,该复数形式在开尔文作为修饰该单位的形容词时添加到度中。
不同的温度计用于不同的温度范围。正如读者可能现在已经猜到的那样,这意味着不同的温度计只会同意固定点。但是,已经仔细选择和校准了一组温度计,因此在实践中这不是一个大问题。
在这种情况下,标准是国际温标,该温标于 1927 年引入,并在 1948 年、1968 年和 1990 年进行了修订。最新的刻度用开尔文刻度的T90表示,从 0.65 K 向上定义。例如,在 0.65 K 到 5.0 K 之间,T90 是根据3He 和4He 的蒸气压温度关系来定义的。不同材料的范围重叠,任何有效的材料都可以在重叠区域用作标准。
回顾一下,热力学系统可能包含某种物质,其数量可以用质量或摩尔数来表示,并占据一定的体积。这些是系统的广延性质。如果物质在所讨论的体积内均匀分布,那么每物质量的体积值可以作为强度性质使用。例如,对于一个称为“摩尔”的量,每摩尔的体积通常被称为“摩尔体积”。类似地,某种物质的每单位质量的体积可能被称为比容。在这种情况下,状态方程可以用来联系三个强度性质:温度、压力和摩尔体积或比容。
一个简单但非常有用的状态方程是理想气体的状态方程。理想气体在热力学中是一个非常有用的概念,因为它是一个只依赖于两个独立性质的简单系统。理想气体是指在除与其他分子完全弹性碰撞之外,没有其他分子间相互作用的气体。对于包含理想气体的封闭系统,其状态可以通过给出压力、温度和摩尔体积中的任何两个值来确定。
考虑一个系统,一个封闭在容器中的理想气体。从初始状态 1 开始,气体的温度为 T1,通过恒压过程将温度改变为 T2,然后进行恒摩尔体积过程,则发现压力的比率与摩尔体积的比率相同。假设初始压力和摩尔体积的值分别为 p1 和 V1,最终压力和摩尔体积的值分别为 p2 和 V2。需要注意的是,我们还没有选择温度的特定标度(例如摄氏温标)。现在,假设我们选择一个标度,使得 T1/T2 = p1/p2,我们可以证明对于理想气体,pV/T 的值是恒定的,因此它遵循气体方程 pV = RT,其中 p 是绝对压力,V 是摩尔体积,R 是一个称为“普适气体常数”的常数。温度 T 是理想气体温标中的绝对温度,该温标与热力学温标一致。热力学温标将在热力学第二定律的陈述之后定义。
这个方程 pV = RT 被称为理想气体的状态方程,也被称为理想气体方程。大多数常见的气体在没有被压缩或冷却到极端状态的情况下,都遵循理想气体方程,因此这是一个非常有用的关系式。我们可以写一个类似的方程,其中对于特定类型的气体,使用比容代替摩尔体积,并使用特定气体常数代替普适气体常数。这样写成 pv = mrT。
在上图中,理想气体在两个不同压力 p1 和 p2 下的体积,针对摄氏温度进行了绘制。如果我们外推这两条直线图,它们会在温度轴上相交于一点 t0,其中 t0 = −273.15 °C。
通过实验,很容易证明热力学温度 T 与摄氏温度 t 之间的关系为:T = t + 273.15。热力学温标的零点是 0 K,当我们讨论热力学第二定律时,它的意义将变得清晰。