FHSST 物理/波/性质
我们已经讨论了一些我们需要了解的简单波的性质。这些只是描述了波具有的特性。现在我们可以继续讨论一些更有趣,也许也更不直观的波的性质。
当波撞击障碍物时,它们会反射。这意味着波会从物体上弹回。声波从墙壁上弹回,光波从镜子中弹回,雷达波从飞机中弹回,蝙蝠如何在夜间飞行并避开电话线等物体。反射的性质非常重要,也非常有用。
(备忘:获得一篇由空中交通管制员撰写的关于雷达的文章) (备忘:获得一篇关于声纳在捕鱼或潜艇中的使用的文章)
当波被反射时,反射过程具有一定的特性。如果波以直角撞击障碍物(备忘:需要图表),那么波会被直接反射回。
如果波以其他角度撞击障碍物,那么它不会被直接反射回。波到达的角度与反射波离开的角度相同。波到达或入射的角度等于波离开或反射的角度。入射角等于反射角
|
(2.1) |
: 入射角 : 反射角
在光学章节中,您将了解光是一种波。这意味着我们刚刚学习的所有性质也适用于光。用镜子很容易演示光的反射。您也可以很容易地证明入射角等于反射角。
如果你直接看进去,你会看到自己......
需要提到入射波、垂直于表面的法线和反射波都在同一个平面上。同样的规则也适用于表面上的折射。
当波从更密集的介质中反射时,它会发生相位变化。这意味着波峰和波谷会交换。
最简单的演示方法是将一根绳子系在某物上。将绳子拉直,然后轻轻弹动一次,使脉冲沿绳子移动。当脉冲(波中单个波峰)撞击绳子绑定的障碍物时,它会反射。反射的波将看起来像波谷,而不是波峰。这是因为脉冲发生了相位变化。固定端就像从更密集的介质中反射一样。
如果绳子的末端没有固定,也就是说它可以上下移动,那么波仍然会被反射,但它不会发生相位变化。
有时波会从一种介质移动到另一种介质。介质是指携带波的物质。在我们第一个例子中,这是水。当介质的特性发生变化时,它会影响波。
让我们从水波从一个深度移动到另一个深度的简单情况开始。波的速度取决于深度。如果波直接从一个介质移动到另一个介质,那么我们应该仔细观察边界。当波峰到达边界并穿过时,它必须在边界的另一侧保持为波峰。这意味着波峰在边界的两侧以相同的时间间隔通过。周期和频率保持不变!但我们说波的速度发生了变化,这意味着它在一个时间间隔内传播的距离不同,即波长发生了变化。
从一个介质到另一个介质,周期或频率不会改变,只有波长会改变。
现在,如果我们考虑一个水波以非 90 度的入射角向介质变化的方向移动,那么我们立即知道,不会有整个波到达。因此,如果一部分波到达并减速,而另一部分波在到达之前仍然以更快的速度移动,那么波前的角度将发生变化。这就是所谓的折射。当波从一种介质移动到另一种介质时,它会弯曲或改变方向。
如果它减速,它会转向垂直方向。
如果波在新的介质中加速,它会远离垂直于介质表面的方向。
当你看到一根从水中伸出的棍子时,它看起来是弯曲的。这是因为来自水面以下的光在离开水时会弯曲。你的眼睛将光线沿直线投影回来,因此物体看起来像是位于不同的位置。
如果两列波相遇,就会发生有趣的事情。波本质上是粒子的集体运动。因此,当两列波相遇时,它们都会试图将它们的集体运动强加于粒子。这会导致非常不同的结果。
如果两列相同的(波长、振幅和频率相同)波都试图形成波峰,那么它们就可以实现它们努力的总和。产生的运动将是一个波峰,其高度是两列波高度的总和。如果两列波都试图在同一个地方形成波谷,那么就会形成一个更深的波谷,其深度是两列波深度的总和。现在,在这种情况下,两列波试图做相同的事情,因此它们会叠加在一起,形成相长干涉。这被称为相长干涉。
如果一个波试图形成波峰,而另一个波试图形成波谷,那么它们就会相互竞争。在这种情况下,它们会互相抵消。波峰的高度减去波谷的深度就是最终的效果。如果波谷的深度与波峰的高度相同,那么什么都不会发生。如果波峰的高度大于波谷的深度,那么就会出现一个更小的波峰,如果波谷更深,那么就会出现一个不太深的波谷。这就是相消干涉。
当两个波以相反的方向穿过彼此移动时,就会发生相长干涉。如果这两个波具有相同的频率和波长,那么就会发生一种特定的相长干涉:驻波可以形成。
驻波是一种看起来不动的干扰,它们停留在同一个位置。让我们来演示一下这是如何发生的。想象一根长绳子,两端都有波沿着它传播。来自两端的波具有相同的振幅、波长和频率,如下图所示
为了避免混淆两个波,我们将左边的波用虚线表示,右边的波用实线表示。当两个波相互靠近时,当它们接触时,两个波的振幅都为零
如果我们等待一小段时间,两个波的末端会相互穿过,然后波会重叠。现在我们知道两个波重叠时会发生什么,我们将它们加在一起得到最终的波。
现在我们知道两个波重叠时会发生什么,我们将它们加在一起得到最终的波。在这张图片中,我们用点线表示两个波,重叠区域中两个波的总和用实线表示
需要注意的是,在这种情况下,有一些点,两个波总是在这些点上发生相消干涉,变成零。如果我们让两个波再移动一小段距离,我们会得到下面的图片
同样,我们必须将两个波在重叠区域加在一起,才能看到波的总和是什么样子。
在这种情况下,两个波已经相互移动了半个周期,但由于它们相位相反,所以它们完全抵消了。点 0 将始终为零,因为两个波相互移动。
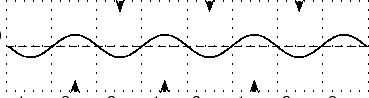
当两个波相互移动,以至于它们在很大区域重叠时,情况看起来就像一个波在原地振动。如果我们关注范围 -4, 4,一旦两个波移动到整个区域,为了更清楚地说明,图片顶部的箭头显示了最大正相长干涉发生的位置。图片底部的箭头显示了最大负干涉发生的位置。
随着时间的推移,波峰变得更小,波谷变得更浅,但它们不会移动。
在某个瞬间,整个区域看起来将完全平坦。
各个点以相同的方式继续运动。
最终,图片看起来像我们开始时的图像经过 x 轴完全反射
然后所有点都开始向后移动。线上的每个点都上下振动,振幅不同。
如果我们将波峰达到最大值和相同波达到最小值这两种情况叠加起来,我们可以看到各个点振动的轨迹。我们称之为驻波的包络线,因为它包含所有点的振动。节点是两个波完全抵消的地方,因为两个波在同一个地方发生相消干涉。反节点是两个波发生相长干涉的地方。
为了使包络线的概念更清楚,让我们画一些箭头来描述沿线的点运动。
包含驻波的介质中的每个点都会上下振动,振动的振幅取决于点的位移。用包络线来描述运动很方便。我们不能为每一个点都画出上下箭头!
如果波从固定端反射,例如将绳子的末端系到一根柱子上,然后沿绳子发送波。固定端将始终是节点。记住:从固定端反射的波会发生相位变化。
波的波长、振幅和速度不会影响这一点,固定端始终是节点。
如果波从可以自由移动的末端反射,它就是一个反节点。例如,将绳子的末端系到一个可以上下移动的环上,环绕在柱子周围。记住:沿绳子发送的波会反射,但不会发生相位变化。
如果发生干涉的波不完全相同,那么这些波将形成一个振幅不断变化的调制模式。振幅中的峰值被称为拍。如果你考虑两个发生干涉的声波,那么你会听到声音响度或强度突然发生拍。
最简单的说明是画出两个不同的波,然后将它们加在一起。你可以用数学方法计算并自己画出它们,看看出现的模式。
这是波 1
现在我们将它加到另一个波,波 2 上
当两个波相加时(用彩色虚线绘制),你可以看到最终的波形
为了更清楚地说明,下面绘制了不含虚线的最终波。注意,波峰之间的距离是相同的,但振幅发生了变化。如果你观察波峰,它们是调制的,也就是说,波峰振幅似乎以另一种波形振动。这就是我们所说的调制。
新波达到的最大振幅等于两个波的总和,就像相长干涉一样。当两个波达到最大值时,它们发生相长干涉。
最小振幅只是两个波振幅的差值,正好与相消干涉一样。
拍的频率等于两个相加波的频率差。这意味着拍频率由以下公式给出
|
(2.2) |
fB : 拍频率(Hz 或 s-1) f1 : 波 1 的频率(Hz 或 s-1) f2 : 波 2 的频率(Hz 或 s-1)
波最有趣的性质之一,也是最有用的性质之一是衍射。当波撞击带有孔的屏障时,只有部分波能穿过孔。如果孔的大小与波的波长相似,就会发生衍射。穿过孔的波不再看起来像直线波前。它会在孔的边缘弯曲。如果孔足够小,它就会像一个圆形波的点源。
这种在孔边缘的弯曲称为衍射。为了说明这种行为,我们从惠更斯原理开始。
惠更斯原理指出,波前上的每个点都像一个点源或圆形波。从每个点发射的波会发生干涉,形成另一个波前,在这个波前上每个点都形成一个点源。一长排以相同频率发射波的点会导致一个直线波前远离这些点移动。
为了理解这意味着什么,让我们考虑很多以相同方向移动的波峰。每条线代表一个波峰。
如果我们在运动方向上的下一波前选择三个点,并使它们各向同性地发射波(即所有方向都相同),我们将得到下面的草图。
我们所画的是,如果波前上的那三个点要发射与运动波前相同频率的波的情况。惠更斯原理说,波前上的每个点都各向同性地发射波,而这些波相互干涉形成下一个波前。
为了查看这是否可行,我们让更多点各向同性地发射波,得到下面的草图。
你可以看到,圆圈(波峰)的线开始重叠成直线。为了使这一点更加清楚,我们重新绘制了草图,用虚线显示将要形成的波前。我们的波前不是完美的直线,因为我们没有从每个点画圆圈。如果我们这样做了,就很难清楚地看到发生了什么。
惠更斯原理是一种应用于波传播问题的分析方法。它认识到,前进波前的每个点实际上都是一个新的扰动的中心,也是一个新的波列的源头,并且整个前进波可以被认为是已经穿过介质的点产生的所有次级波的总和。这种对波传播的看法有助于更好地理解各种波现象,例如衍射。
现在,如果我们让波前撞击一个有洞的屏障,那么只有波前上进入洞的点才能继续向前发射波 - 但是由于很多波前都被去掉了,所以洞边缘的点发射的波会绕着边缘弯曲。
撞击(撞击)墙壁的波前不能继续向前移动。只有进入间隙的点才能移动。如果你使用惠更斯原理,你可以看到效果是波前不再是直线。
Riaan 注:仍然找不到这张图片,必须从 pdf 中获取。
例如,如果两个房间通过一个敞开的门连接,在一个房间的远角发出声音,那么另一个房间里的人会听到声音,就好像声音是从门口发出的。就第二个房间而言,门口振动的空气是声音的来源。光线经过障碍物边缘也是如此,但由于可见光的波长很短,因此不容易观察到这一点。
这意味着当波穿过小孔时,它们似乎会绕着侧面弯曲,因为波前上没有足够的点形成另一个直波前。这种绕着侧面弯曲,我们称之为衍射。
色散是波的一种性质,其中波在介质中的速度取决于波长。因此,如果两个波进入相同的色散介质,并且具有不同的波长,那么它们在该介质中的速度将不同,即使它们都以相同的速度进入。