数学/几何/勾股定理著名定理

勾股定理：两条直角边上正方形的面积之和等于斜边上正方形的面积。

在一个直角三角形中，斜边的平方等于其他两边的平方和。符号上，对于直角三角形ABC，直角位于C，$AC^{2}+BC^{2}=AB^{2}$，或 $a^{2}+b^{2}=c^{2}$，其中c是斜边。

欧几里得的证明

此证明使用以下内容

• 直角的定义
• 平行的定义
• 正方形的定义
• 边长为x的正方形的面积为x²
• 正方形的所有角都是直角
• 在同一点上，同一侧与同一直线成直角的线段，在另一侧形成一条直线
• 所有直角都相等
• 如果两个三角形的两边和它们之间的角分别相等，则这两个三角形全等
• 全等三角形的面积相等
• 三角形的面积是同一平行线之间同底边平行四边形面积的一半

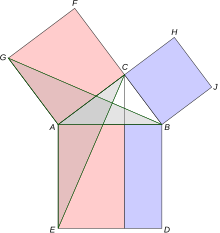
欧几里得在他的几何原本第一卷命题47中给出了勾股定理的证明。

设ABC为直角三角形，直角位于C。构造正方形ABDE、ACFG和BCHJ，以及垂直于AB和ED的直线CKL。

考虑三角形GAB和CAE。对于这两个三角形，边GA和CA相等，因为它们是正方形ACFG的边。同样，边AB和AE相等，因为它们是正方形ABDE的边。此外，角GAB和CAE相等，因为它们都包含角CAB加上正方形的一个直角。因此，三角形GAB和CAE全等。

三角形GAB的面积是正方形ACFG的一半，因为它们共用边GA，点B与正方形的对面FC共线。（这可以通过观察将GAB剪切产生GAC来更清楚地看到，GAC的面积明显是ACFG的一半，并且由于剪切保留面积，因此GAB的面积也是如此。）

同样，三角形CAE的面积是矩形AKLE的一半，因为它们共用边AE，点C与KL共线。

但GAB和CAE的面积相等。因此，正方形ACFG和矩形AKLE的面积相等。

用同样的论证，正方形BCHJ的面积等于矩形BKLD的面积。两个矩形AKLE和BKLD构成正方形ABDE，因此正方形ABDE的面积等于ACFG的面积加上BCHJ的面积。