分形/共形映射

共形映射

以下是共形映射应用于图片的例子。这种技术是域着色的推广，其中域空间不是由固定的无限色轮着色，而是由一个有限的图片平铺平面。教学上的意义在于有一个来自网络摄像头的图片流，允许更多的交互性和更丰富的反馈循环。

共形映射

一个钟表的图片。

一个钟表经过相似变换后的图片。

共形映射是保持角度的平面变换。平面可以用笛卡尔坐标系参数化，其中一个点表示为$(x,y)\in \mathbb {R} ^{2}$，但对于共形映射，最好将它理解为复平面，其中点表示为$x+i\,y\in \mathbb {C}$.

在复坐标系中，乘以一个实数r对应一个同质变换，乘以一个单位数$e^{i\theta }$对应一个角度为θ的旋转，乘以一个通用的复数$z=r\,e^{i\theta }$对应一个相似映射。

全纯函数是一个共形映射，因为它在局部是一个相似映射$f(z)=a\,(z-z_{0})+b+o(z-z_{0})$，其中$a=f'(z_{0})$是导数，$b=f(z_{0})$是f在z₀的值。导数是变换的局部缩放因子。

在相似性之后，相似性具有常数导数函数，多项式，特别是单项式$z\mapsto z^{k}$是最简单的全纯函数。它的导数是$z\mapsto k\,z^{k-1}$，它在原点为零；因此，相关的映射只有在远离原点时才是共形的。

我们面临的一个问题是，全纯函数通常不是单射的：例如，考虑单项式$z^{k}$，例如，k个不同的点被映射到同一个值。

考虑到用钟表图片平铺的平面，当平方时，它变成以下模糊的图片

一个钟表平方。注意每个点都被覆盖了两次。

我们看到，中心圆盘是全局保存的，被映射到自身，但每个点（除了零）都被覆盖了两次，使得图片变得模糊。例如，+1（在 3 点钟位置）和 −1（在 9 点钟位置）都被发送到 +1（在中间右侧），+i（中午）和 i（6 点钟位置）都被发送到 −1（在中间左侧）。

为了获得一个单射应用，我们可以将自己限制在例如正实半平面或负实半平面。

负实半平面平方。

正实半平面平方。

从更远的地方看，我们得到了整个平铺的相同大图。

• 
  负实半平面平方。
• 
  钟表平方：共形但不是单射。
• 
  正实半平面平方。

拉回

盐度被描绘成一个原像

为了获得一个漂亮的共形图片，考虑不是直接像而是原像会更容易更自然。

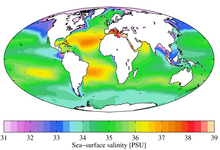
这正是许多地球信息被描绘的方式。例如，将温度值设置为每个点的地图可以通过将地球仪上的每个点用颜色绘制来描绘，该颜色指定该点温度函数的值。目标空间，即温度空间，从蓝色（较小值）到红色（较大值）被绘制。这里使用了相同的绘图技术，但目标空间不再是 1 维实数空间；它不是一条线，而是整个平面。

图片不再表示应用程序的域，而是它的目标空间。点 z 根据像素 f(z) 着色。

由 $z\mapsto z^{2}$ 进行的反向映射。

注意重复：点 z 和 −z 被着色相同，因为它们都被映射到同一个图像 z²。

一个 4 次多项式。注意它导数的零点。简单的零点看起来没什么特别。

由 $z\mapsto z^{3}$ 进行的反向映射。

同样，k 阶单项式将 k 个不同的点映射到同一个图像。

可以通过描绘它的反向映射来理解关于保角映射的许多有用信息。由于正向缩放因子是导数，反向缩放因子是导数的“逆”。因此，在函数导数的零点处发生了一些非常特殊的事情，缩放因子变得无穷大，并且它显示出来了。此外，零点的阶数可以通过特征围绕奇点的重复次数来读出。我们也注意到，当导数为实数且为正时，图片是“直立”的，而当导数为实数且为负时，图片是“倒置”的。当我们将自己限制在实轴上时，我们可以找出实函数图形的草图。我们也注意到拐点是缩放因子的最小值或最大值。

反演，极点

在全纯函数之后，局部保角映射还包括亚纯函数，并且它们的极点的位置和阶数可以读出。

反演 $z\mapsto 1/z$.

反演（详细视图）。

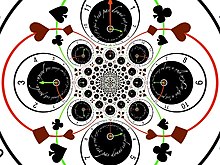
反演 $z\mapsto 1/z$ 在零点处有一个简单的极点。它是一个莫比乌斯变换 $z\mapsto {\frac {az+b}{cz+d}}$，其中 a、b、c 和 d 是四个复数，使得 $ad-bc\neq 0$，因此它将圆和线映射到圆和线。特别是，水平线和垂直线变成了过零点的圆。反演交换了单位圆的内部和外部。

两个极点在 ±1/2。

一个二阶极点 $z\mapsto 1/z^{2}$.

像零点一样，极点的阶数也可能高于简单极点。圆一般情况下只是无穷小地被保留。我们可以将高阶极点视为几个简单极点汇集在一起。

对数和指数

指数映射 $z\mapsto e^{z}$。注意同态和旋转不变性，对应于目标格子的水平（实数）和垂直（纯虚数）平移不变性。

对数映射 $z\mapsto \log(z)$。注意单位圆被垂直地解开。

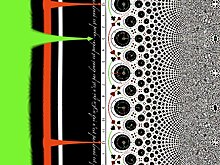
复分析和地图学中一个非常重要的映射是从直角坐标 (x,y) 到极坐标 (r,θ) 的变换。这个变换是由对数/指数函数对实现的，它们互为倒数 ($\log(\exp(z))=z$)。实际上，

$\log(r\,e^{i\theta })=\log(r)+i\theta$ 将 (r, θ) 映射到 (x = log(r), y = θ)，而 $\exp(x+i\,y)=\exp(x)\,e^{i\,y}$ 将 (x, y) 映射到 (r = exp(x), θ = y)。

在图中，对数将以原点为中心的圆展开成垂直线，并将射线映射到水平线。相反，指数将垂直线包裹成同心圆，并将水平线映射到通过原点的射线。请注意，对数在零处趋于无穷大，但其增长速度比反演慢得多。

改变格子的基底，可以得到螺旋变化。作为极点和零点，可以添加对数奇点。

• 
• 
• 
• 

本质奇点

本质奇点 $z\mapsto e^{1/z}$.

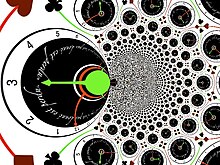
解析函数会遇到另一种类型的奇点，例如本质奇点 $z\mapsto e^{1/z}$ 在 $z=0^{-}$ 为零，并具有零点累积，在 $z=0^{+}$ 具有极点累积。

收敛半径

解析函数可以求和成幂级数。在给定点，其泰勒级数具有收敛半径。比较函数及其截断泰勒级数的反向映射，我们可以说明这个概念。

• 
  正切函数在每个 kπ/2 处有一个简单的极点。它在无穷远处有一个本质奇点。
• 
  它在 0 处的 7 阶泰勒级数在其收敛圆盘中是一个很好的近似。

程序

• Don Marshall 的 zipper
• ConformalMaps，Samuel S. Watson 在 Julia 中编写
• 使用 Zipper 算法数值逼近共形映射
• RoyWiggins 实现的 Julia 包，用于数值共形映射的 zipper 算法

外部链接

• 维基百科中的共形映射类别
• 这些图片使用以下方式变形 Java 小程序；另一个 版本 可用于 Mac OS X，它可以变形来自网络摄像头的视频流。java -d32 -jar ComplexMap.jar。这很有趣。使用 Java 实验数学工具 库。
• John H. Mathews 的共形映射模块
• 许多共形映射的交互式可视化
• 用于可视化共形映射的 Java 小程序
• 共形映射，Michael Trott，Wolfram 演示项目。
• Java 小程序，Jürgen Richter-Gebert 使用 Cinderella。
• 共形网络摄像头 基于 Cinderella。使用您的网络摄像头以交互方式绘制本页上的示例，使用您的网络摄像头馈送。
• conformal_map，Yue Liu 编写的

另请参见

• 对圆盘进行平方运算的解析方法
• 梅比乌斯变换