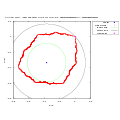
分形/复平面上的迭代/临界轨道

定义

正向轨道 的 临界点 被称为临界轨道。

重要性

临界轨道非常重要，因为每个吸引 周期轨道 都吸引一个临界点，因此研究临界轨道有助于我们理解 法图集 中的动力学。

$z_{0}=z_{cr}=0\,$

$z_{1}=f_{c}(z_{0})=c\,$

$z_{2}=f_{c}(z_{1})=c^{2}+c\,$

$z_{3}=f_{c}(z_{2})=(c^{2}+c)^{2}+c\,$

$...\,$

此轨道落入 吸引周期循环 中。

形状

形状类型和动力学之间的关系

• n 臂螺旋：吸引或排斥 n 周期轨道（循环）
• 闭合曲线：西格尔圆盘（旋转）
• n 臂星形 = 时期 n 抛物根

临界轨道的形状可以显示动力学的类型和周期

• 
  抛物 n 臂星形
• 
  西格尔圆盘（闭合曲线）
• 
  弱吸引不动点 = 长螺旋

水平集

临界轨道的点（包括临界点和不动点 = 有限吸引子）位于水平曲线上，就像乐谱上的音符（曲线上的点）。

如何计算吸引半径 (AR) 以获得这种效果？

• 
  周期 1 抛物线
• 
  周期 1 吸引
• 
• 
  周期 2 吸引

代码

"https://github.com/conanite/rainbow/blob/master/src/arc/rainbow/spiral.arc
 This software is copyright (c) Conan Dalton 2008. Permission to use it is granted under the Perl Foundations's Artistic License 2.0.
 This software includes software that is copyright (c) Paul Graham and Robert Morris, distributed under the Perl Foundations's Artistic License 2.0.
 This software uses javacc which is copyright (c) its authors
"
(def plot (plt c)
  (with (z 0+0i
         n 0
         repeats 0)
    (while (and (small z) (< n 10000) (< repeats 1000))
      (assign n       (+ n 1)
              z       (+ c (* z z))
              repeats (if (apply plt (complex-parts z))
                          (+ repeats 1)
                          0)))))

图片

• commons 上的临界轨道图片
• 作者：Mike Croucher
• Chris King
• Kerry Mitchel：心形边界轨道
• Anne M. Burns 撰写的《可视化曼德布洛特集中的逃逸路径》
• Stefan Zenker

列表

• 临界轨道
• Lori GardiThe Mandelbrot set and the fractal nature of light, the Universe, and everything by
• Lori Gardi 撰写的《曼德布洛特集作为准黑洞》
• Stefan Bion 撰写的《曼德布洛特 Z 轨道》
• Stefan Bion 撰写的《绘制列表中的轨道》
• Conan 使用 Rainbow 编写的图片
  • 简介
  • 示例
• Stefan Forcey 撰写的《曼德布洛特序列和轨道》
• P. Alcover 发表的 2017 年作品《曼德布洛特集轨道图中的莫尔干涉》

程序

• Geogebra（交互式）
  • Ben Sparks 撰写的《曼德布洛特迭代轨道》
  • Hüseyin KAVAK 撰写的《曼德布洛特集》
• Stefan Forcey 撰写的《Java 脚本》

视频

• Fractal Woman 撰写的《曼德布洛特集作为涡流发生器》

参见

• 在圆盘上散布点