分形/数学/群
这里可以找到分形和群之间关系的例子。[1]
"群论非常有用,因为它通过抽象的力量找到了不同事物之间的共同点。"[2]
自相似群的代数结构和多项式的动力学性质之间存在着重要的联系。
群论
- 几何的
- 组合的
- 计算的
字母表 它是一组有限的符号 x
自动机是顺序机器的基本抽象数学模型。 不同类型的自动机
- 识别自动机,
- 图灵机
- 摩尔机
- 米利机,
- 元胞自动机
- 下推自动机
自动机有两种视觉呈现
- 一个状态表,描述了到下一个状态的转换和输出,
- 一个状态图。
等价类 集合 X 中的元素 a 是集合 X 中所有与 a 等价的元素的子集
p-adic 数字是 0 到 p − 1(含)之间的自然数。
一个 p-adic 整数是一个 p-adic 数字的序列
数字的 n-adic 扩展[3]
二进制整数或二元整数或 2-adic 整数
其中 a 是二进制字母表 X ={0,1} = (0, .. ,2-1) 的一个元素
施赖尔图
自动机的摩尔图(或摩尔机的状态图)它是一个有向带标签的图,它有
- 顶点(节点)用自动机/基本群的生成元的状态来识别
- 边(带箭头的线)显示状态转换,
- 标签 : (输入, 输出) 是 X 中元素的有向对
"群是服从一组严格规则的物体集合,这些规则在操作作用于它们时适用。"[4]
一个群 是代数结构
, 其中
- 是一个非空集合
- 表示一个称为群运算的二元运算
它必须服从以下规则(或公理)
- 封闭性,
- 结合律
- 单位元
- 逆元
- 交换律[5]
单位元 : "群必须有一个元素充当单位元。单位元的特征是它与群运算下的任何其他成员组合时,都不会改变该成员。"[6]
逆元 : "群的每个成员或元素必须有一个逆元。当一个成员与它的逆元在群运算下组合时,结果是单位元"[7] 封闭性 : "这意味着每当两个群成员在群运算下组合时,结果都是群的另一个成员"[8]
结合律 : "如果我们取三个或更多群成员的列表并将其两个两个地组合,那么从列表的哪一端开始并不重要"[9]
自动机群 = 由自动机生成的群
FR = 泛递归群
IMG = 迭代单值群
[edit | edit source]其中顶点 通过边与 相连。
自相似群
[edit | edit source]机器
[edit | edit source]有限状态机[12]
- 米利机[13]
- 摩尔机
多项式
[edit | edit source]后临界有限多项式 : 临界点的轨道是有限的。当临界点是周期性的或前周期性的时,就会出现这种情况。[14]
关系
[edit | edit source]等价关系 ~ 在集合 X 上
- 它是在 X 上的一个二元关系,是自反的、对称的和传递的
- 它在集合 X[15] 上诱导出一个划分 P,划分为几个不相交的子集,称为等价类
序列
[edit | edit source]ks = 揉捏序列(s)
词语
[edit | edit source]在字母表 X 上的词语 w 是字母表 X 中的任何符号序列。词语可以是
- 无限的
- 有限
- 空词 = 长度为零的词:
表示以 开头的词。
"二次有理映射的迭代单梦群,其中后临界集的大小最多为 3,排列成表格。
大多数的代数结构尚未得到很好的理解。" [16]
| f(z) | 标准作用 | 核 | 机器 | 群 | 注释 |
|---|---|---|---|---|---|
| 加法机 | 二进制加法群 | ||||
| 巴西利卡群 | |||||
| 与切比雪夫多项式 T2 共轭 | |||||
| [17] | 汉诺塔群 | ||||
| 谢尔宾斯基三角形 | |||||
| 汤普森类群[18] | 中间增长 |
其中
- 是一个排列
Group Explorer 是抽象代数课堂的数学可视化软件。 [19]
/usr/share/gap/bin/gap.sh
如果系统无法加载包,请安装库、包并编译它们(nq、pargap、fr)。运行测试
Read( Filename( DirectoriesLibrary( "tst" ), "testinstall.g" ) );
加载 Laurent Bartholdi 的 fr 包 [22]
LoadPackage("fr");
运行 fr 测试
Read( Filename( DirectoriesLibrary( "pkg/fr/tst" ), "testall.g" ) );
GAP 和 fr 包可以使用 Mandel、ImageMagic、graphviz 或 rsvg-view 等外部程序绘制和显示图像。
绘制 [23]
Draw(NucleusMachine(BasilicaGroup));
- 创建 m(米利机或元素 m)的图描述。 它使用 graphviz 包 [24] 中的 dot 程序转换为 Postscript。
- 使用命令行程序 display(来自 ImageMagick)或 rsvg-view 在单独的 X 窗口中显示图像。 [25] 这在 UNIX 系统上有效。
可以右键单击图像以查看显示程序的本地菜单。
如果 Draw 函数的第二个参数(文件名)存在,则图将以 dot 格式保存到该文件名下。
Draw(NucleusMachine(BasilicaGroup),"a.dot");
将输出保存到 a.dot 文件。dot 文件是一个描述图的文本文件,以 dot 语言编写。
digraph MealyMachine {
a [shape=circle]
b [shape=circle]
c [shape=circle]
d [shape=circle]
e [shape=circle]
f [shape=circle]
g [shape=circle]
a -> a [label="1/1",color=red];
a -> a [label="2/2",color=blue];
b -> a [label="1/1",color=red];
b -> d [label="2/2",color=blue];
c -> a [label="1/1",color=red];
c -> e [label="2/2",color=blue];
d -> a [label="1/2",color=red];
d -> b [label="2/1",color=blue];
e -> c [label="1/2",color=red];
e -> a [label="2/1",color=blue];
f -> a [label="1/2",color=red];
f -> g [label="2/1",color=blue];
g -> f [label="1/2",color=red];
g -> a [label="2/1",color=blue];
}
This a.dot file can be converted to other formats using command line program dot. For example in ps file :
dot -Tps a.dot -o a.ps
或 png 文件
dot -Tpng a.dot -o a.png
或 svg
dot -Tsvg a.dot -o a.svg
外部角
[edit | edit source]来自 FR 包的函数
ExternalAngle(machine)
返回:识别机器的外部角。
如果机器是单临界多项式的 IMG 机器,则该函数计算落在临界值的外部角。
gap> z := Indeterminate(COMPLEX_FIELD,"z");
z
gap> r := P1MapRational(z^2-1); # Basilica Julia set
<P1 mapping of degree 2>
gap> m:=IMGMachine(r);
<FR machine with alphabet [ 1, 2 ] and adder FRElement(...,f3) on Group( [ f1, f2, f3 ] )/[ f2*f1*f3 ]>
gap> ExternalAngle(m);
{2/3}
Elements(last); # More precisely, it computes the equivalence class of that external angle under ExternalAnglesRelation
[ 1/3, 2/3 ]
另一个例子
gap> m:= PolynomialIMGMachine(2,[1/7]); # the machine descibing the rabbit : degree=2,
gap> ExternalAngle(m);
{2/7}
gap> Elements(last);
[ 1/7, 2/7 ]
机器
[edit | edit source]PolynomialIMGMachine
[edit | edit source]PolynomialIMGMachine(d, per[, pre[, formal]])
此函数创建一个 IMG 机器,它描述一个拓扑多项式。该多项式在外部角语言中以符号方式描述。
d 是多项式的次数。
per 是角度列表
pre 是预角度列表。
角度是理性数,以模 1 计。per 或 pre 中的每个条目都是一个理性数(解释为一个角度),或者是一个角度列表 [a1,...,ai],使得 da1 = ... = dai。per 中的角度是落在法图分量根部的角度,而 pre 中的角度落在 Julia 集的其他点上。
gap> m:=PolynomialIMGMachine(2,[1/3],[]); # the Basilica <FR machine with alphabet [ 1, 2 ] and adder FRElement(...,f3) on Group( [ f1, f2, f3 ] )/[ f3*f2*f1 ]> gap> Display(m); G | 1 2 ----+---------+---------+ f1 | f1^-1,2 f2*f1,1 f2 | f1,1 <id>,2 f3 | f3,2 <id>,1 ----+---------+---------+ Adding element: FRElement(...,f3) Relator: f3*f2*f1
gap> Display(PolynomialIMGMachine(2,[],[1/6])); # z^2+I G | 1 2 ----+---------------+---------+ f1 | f1^-1*f2^-1,2 f2*f1,1 f2 | f1,1 f3,2 f3 | f2,1 <id>,2 f4 | f4,2 <id>,1 ----+---------------+---------+ Adding element: FRElement(...,f4) Relator: f4*f3*f2*f1
PostCriticalMachine
[edit | edit source]PostCriticalMachine(f)
返回:f 的后临界轨道的米利机。该函数在字母表 [1] 上构建一个米利机 P,它描述了 f 的后临界集。
gap> z := Indeterminate(Rationals,"z");; gap> m := PostCriticalMachine(z^2); <Mealy machine on alphabet [ 1 ] with 2 states> gap> Display(m); | 1 ---+-----+ a | a,1 b | b,1 ---+-----+ gap> Correspondence(m); [ 0, infinity ]
它实际上是一个具有恒定出度的定向图 1。
Draw(m);
gap> m := PostCriticalMachine(z^2-1);; Display(m); Correspondence(m); | 1 ---+-----+ a | c,1 b | b,1 c | a,1 ---+-----+ [ -1, infinity, 0 ]
Kneading 序列
[edit | edit source]KneadingSequence(angle)
"此函数将理性角转换为 kneading 序列, [26] 用于描述二次多项式。 [27]"(来自 fr 文档)
KneadingSequence(1/7);
给出
[ 1, 1 ]
"如果角度在 [1/7, 2/7] 之间,并且设置了标记选项,则 kneading 序列将用 A、B、C 中的标记进行装饰。"(来自 fr 文档)
KneadingSequence(1/5:marked);
给出
[ "A1", "B1", "B0" ]
根点的射线
[edit | edit source]ExternalAnglesRelation(degree, n)
"此函数返回...所有落在度数乘以角乘法下共同周期点的所有外部角对。"(来自 fr 文档)换句话说,它给出了落在曼德布罗特集的周期 n 双曲分量的根点的外部射线转弯中的角度。 [28]
对于复二次多项式(度数 = 2)和周期 3
ExternalAnglesRelation(2,3); <equivalence relation on Rationals >
它需要一个额外的命令
EquivalenceRelationPartition(last);
并给出
[ [ 1/7, 2/7 ], [ 1/3, 2/3 ], [ 3/7, 4/7 ], [ 5/7, 6/7 ] ]
此列表有 4 个元素
- 3 对周期 3 角 i/7
- 1 对周期 2 角 i/3
内部地址
[edit | edit source]"此函数返回所有在角度加倍下周期最多为 n 的周期点的内部地址。这些内部地址描述了从着陆点到曼德布罗特集中的主心形路径上的突出双曲分量。"(来自 fr 文档)
将其与 **角度内部地址** [29] 进行比较
注意角度是分母为(奇数)的分数
其中 n 是周期,d 是分母
周期 2
[edit | edit source]
AllInternalAddresses(2); [ [ ], [ [ 1/3, 2/3, 2 ] ] ]
对于周期 1,列表为空。
[]
对于周期 2,它给出
[ [ 1/3, 2/3, 2 ] ]
其中包含一个子列表
[1/3, 2/3, 2]
它描述了曼德布罗特集的周期 2 双曲分量,外部射线 1/3 和 2/3 落在其根点上。 [30]
周期 3
[edit | edit source]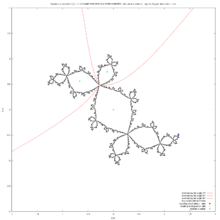

AllInternalAddresses(3); [ [ ], [ [ 1/3, 2/3, 2 ] ], [ [ 1/7, 2/7, 3 ], [ 3/7, 4/7, 3, 1/3, 2/3, 2 ], [ 5/7, 6/7, 3 ] ] ]
对于周期 3,我们有之前的周期 2 地址和周期 3 的新列表
[ [ 1/7, 2/7, 3 ], [ 3/7, 4/7, 3, 1/3, 2/3, 2 ], [ 5/7, 6/7, 3 ] ]
它有 3 个元素(子列表)。
第一个元素
[ 1/7, 2/7, 3 ]
描述了周期 3 双曲分量,射线 1/7 和 2/7 落在其根 c=0.64951905283833*%i-0.125 上,它位于主心形的边界上,内部角 = 1/3
第二个元素
[ 3/7, 4/7, 3, 1/3, 2/3, 2 ]
描述了周期 3 分量,射线 3/7 和 4/7 落在其根点上。要找到它,必须通过周期 2 分量。
因为对于醒着的 c 在 (3/7, 4/7) 中,动态射线 3/7 和 4/7 在一个排斥周期点处一起着陆,所以它也描述了飞机 Julia 集[31][32],其着陆角为 [1/3, 2/3],周期为 2。
第三个元素
[ 5/7, 6/7, 3 ]
描述周期为 3 的双曲分量,其射线 5/7 和 6/7 在其根点处着陆(它是 c=-0.64951905283833*%i-0.125,位于主心形边界上,内部角 = 2/3)。
蜘蛛算法
[edit | edit source]蜘蛛算法[33] 构造了具有指定组合学的多项式。
论文
- 蜘蛛算法 - John H. Hubbard 和 Dierk Schleicher 的论文[34]
- Claude Heiland-Allen 的在线文章[35]
- Yuval Fisher 的原始论文[36]
- Tore Moller Jonassen 的论文[37]
- Gregory A. Kelsey 的论文[38]
- SUZANNE HRUSKA BOYD 和 CHRISTIAN HENRIKSEN 的多项式匹配的 MEDUSA 算法
另请参阅程序
谷歌搜索:"蜘蛛算法" 多项式
有理函数
[edit | edit source]RationalFunction(m)
它返回一个有理函数 f,其关联的机器为 m,或者描述 f 可实现性的 Thurston 障碍的记录。
gap> m := PolynomialIMGMachine(2,[1/3],[]); # the basilica <FR machine with alphabet [ 1, 2 ] and adder FRElement(...,f3) on Group( [ f1, f2, f3 ] )/[ f3*f2*f1 ]> gap> RationalFunction(m); z^2-1.
gap> m:=PolynomialIMGMachine(2,[1/7]); # the rabbit <FR machine with alphabet [ 1, 2 ] and adder FRElement(...,f4) on Group( [ f1, f2, f3, f4 ] )/[ f4*f3*f2*f1 ]> gap> RationalFunction(m); z^2 + (-0.12256116687667946+I*0.74486176661942738)
Delaunay 三角剖分
[edit | edit source]gap> LoadPackage("fr");
gap> z := Indeterminate(COMPLEX_FIELD);
x_1
gap> f := z^2-1;
x_1^2-1.
gap> m := IMGMachine(f);
<FR machine with alphabet [ 1, 2 ] and adder FRElement(...,f3) on Group( [ f1,\ f2, f3 ] )/[ f2*f1*f3 ]>
gap> Spider(m);
<marked sphere on <triangulation with 6 vertices, 24 edges and 8 faces> marked by [ f1, f2, f3 ] -> [ f1^-1*f2^-1, f1, f2 ]>
gap> Draw(last:julia);
或者
gap> LoadPackage("fr");
gap>z := Indeterminate(COMPLEX_FIELD,"z");
gap> r := P1MapRational(z^2-1);
<P1 mapping of degree 2>
gap> IMGMachine(r); #I Post-critical points at [ P1Point("-1+0i"), P1Point("0+0i"), P1Point("P1infinity") ]
<FR machine with alphabet [ 1 .. 2 ] and adder FRElement(...,f3) on Group( [ f1, f2, f3 ] )/[ f2*f1*f3 ]>
gap> Spider(last);
<marked sphere on <triangulation with 6 vertices, 24 edges and 8 faces> marked by [ f1, f2, f3 ] -> [ f1^-1*f2^-1, f\ 1, f2 ]>
gap> Draw(last:julia);
在球体上绘制动态平面,并标记 Delaunay 三角剖分。可以用鼠标实时旋转球体。
参考文献
[edit | edit source]- ↑ 维基百科上的群论
- ↑ mathilluminated:第 6 单元 对称之美
- ↑ 维基百科:p-adic 数
- ↑ learner.org 课程:mathilluminated - 对称
- ↑ 初等群论
- ↑ learner.org 课程:mathilluminated - 对称
- ↑ learner.org 课程:mathilluminated - 对称
- ↑ learner.org 课程:mathilluminated - 对称
- ↑ learner.org 课程:mathilluminated - 对称
- ↑ 维基百科上的迭代单梦群
- ↑ 迭代单梦群简介 作者:Sébastien Godillon
- ↑ 计算机科学 Logo 风格 第 3 卷:超越编程 作者:Brian Harvey
- ↑ 维基百科:Mealy 机
- ↑ Alfredo Poirier:关于后临界有限多项式 第一部分:临界肖像
- ↑ 维基百科:等价关系
- ↑ 从分形群到分形集 作者:Laurent Bartholdi, Rostislav I. Grigorchuk, Volodymyr V. Nekrashevych
- ↑ 从自相似群到自相似集和谱 作者:Rostislav Grigorchuk, Volodymyr Nekrashevych, Zoran Sunic
- ↑ 树状 Julia 集的群 作者:Will Smith
- ↑ Explorer
- ↑ 维基百科上的 GAP 软件
- ↑ 维基百科上的 CAS
- ↑ Laurent Bartholdi 为 GAP CAS 编写的 FR 包
- ↑ Laurent Bartholdi 编写的 fr 包中的 Draw 函数
- ↑ graphviz - 图形可视化软件
- ↑ librsvg - 免费的开源 SVG 渲染库
- ↑ 单峰映射和揉捏理论 作者:Warren Weckesser
- ↑ 揉捏序列的可接受性和二次多项式的 Hubbard 树结构 作者:HENK BRUIN 和 DIERK SCHLEICHER
- ↑ Mandelbrot 集周期 p 分量的根点的参数射线
- ↑ Mandelbrot 集中的内部地址和多项式的不可约性 作者:Dierk Schleicher
- ↑ Mandelbrot 集周期 p 分量的根点的参数射线
- ↑ Julia 小矮人缩放。"飞机" 结构 作者:Evgeny Demidov
- ↑ n-Category Café 关于 Benoit Mandelbrot 的讨论
- ↑ 蜘蛛算法
- ↑ 算法 - John H. Hubbard 和 Dierk Schleicher 的论文
- ↑ 重现蜘蛛 作者:Claude Heiland-Allen
- ↑ Yuval Fisher 的原始论文
- ↑ Tore Møller Jonassen
- ↑ Gregory A. Kelsey 的论文
书籍



![{\displaystyle [a]_{X}=\{x\in X|x\sim a\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de7b4d1ef07c980cb62a2a568b3992d5502b8379)

























