本文描述了周期点 的某些复二次映射 。一个映射 是根据变量本身的先前值或值计算变量值的公式;一个二次 映射是涉及先前值被提升到幂 一和二的映射;一个复 映射是一个变量和参数都是复数 的映射。一个周期点 是指映射中变量的值,该值在固定长度的间隔后会重复出现。
这些周期点在法图 和朱利亚集 理论中发挥着作用。
让
f c ( z ) = z 2 + c {\displaystyle f_{c}(z)=z^{2}+c\,} 是复二次映射 ,其中 z {\displaystyle z} c {\displaystyle c} 复数 。
在符号上, f c ( k ) ( z ) {\displaystyle f_{c}^{(k)}(z)} k {\displaystyle k} 复合 的 f c {\displaystyle f_{c}} k {\displaystyle k} 导数 的 f c {\displaystyle f_{c}} f c . {\displaystyle f_{c}.} k 次迭代 之后的的值。因此
f c ( k ) ( z ) = f c ( f c ( k − 1 ) ( z ) ) . {\displaystyle f_{c}^{(k)}(z)=f_{c}(f_{c}^{(k-1)}(z)).} 复二次映射的周期 为 p {\displaystyle p} 动力学平面 上的点 z {\displaystyle z}
f c ( p ) ( z ) = z , {\displaystyle f_{c}^{(p)}(z)=z,} 其中 p {\displaystyle p} 整数 。
我们可以引入一个新函数
F p ( z , f ) = f c ( p ) ( z ) − z , {\displaystyle F_{p}(z,f)=f_{c}^{(p)}(z)-z,} 所以周期点是 零点 函数 F p ( z , f ) {\displaystyle F_{p}(z,f)}
F p ( z , f ) = 0 , {\displaystyle F_{p}(z,f)=0,} 这是一个 次数 为 2 p . {\displaystyle 2^{p}.}
描述周期点的多项式 F p ( z , f ) {\displaystyle F_{p}(z,f)} 次数 为 d = 2 p {\displaystyle d=2^{p}} 代数基本定理 它正好有 d = 2 p {\displaystyle d=2^{p}} 重数 。
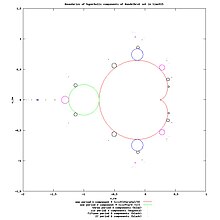
水平轴上周期点的稳定性指标 参数平面区域的边界,这些区域具有周期为 1-6 的吸引轨道 基于 复二次多项式 的离散动力系统的临界轨道。它趋向于弱 吸引 的 不动点 ,其中 abs(乘子) = 0.99993612384259 有理映射 f {\displaystyle f} z 0 {\displaystyle z_{0}} p {\displaystyle p} m ( f p , z 0 ) = λ {\displaystyle m(f^{p},z_{0})=\lambda }
m ( f p , z 0 ) = λ = { f p ′ ( z 0 ) , if z 0 ≠ ∞ 1 f p ′ ( z 0 ) , if z 0 = ∞ {\displaystyle m(f^{p},z_{0})=\lambda ={\begin{cases}f^{p\prime }(z_{0}),&{\mbox{if }}z_{0}\neq \infty \\{\frac {1}{f^{p\prime }(z_{0})}},&{\mbox{if }}z_{0}=\infty \end{cases}}} 其中 f p ′ ( z 0 ) {\displaystyle f^{p\prime }(z_{0})} f p {\displaystyle f^{p}} z {\displaystyle z} z 0 {\displaystyle z_{0}} 导数 。
由于乘数在给定轨道上的所有周期点处都相同,因此被称为周期 轨道 的乘数。
乘数为
一个复数;
在任何有理映射在其不动点处的共轭下是不变的;[ 1]
用于检查周期点(也包括不动点)的稳定性,其 **稳定性指数** 为 a b s ( λ ) . {\displaystyle abs(\lambda ).\,} 周期点[ 2]
当 a b s ( λ ) < 1 ; {\displaystyle abs(\lambda )<1;} 当 a b s ( λ ) = 0 ; {\displaystyle abs(\lambda )=0;}
当 0 < a b s ( λ ) < 1 ; {\displaystyle 0<abs(\lambda )<1;}
当 a b s ( λ ) = 1 ; {\displaystyle abs(\lambda )=1;} 当 λ {\displaystyle \lambda } 单位根 时,为有理中性点或抛物线点;
无理中性点 当 a b s ( λ ) = 1 {\displaystyle abs(\lambda )=1}
当 a b s ( λ ) > 1. {\displaystyle abs(\lambda )>1.} 周期点
是吸引点的,总是位于 Fatou 集 中;
是排斥点的,位于 Julia 集中;
是中性不动点的,可能位于其中一个或另一个。[ 3] solve these equations using numerical methods for solving polynomials - and even something simple such as Newton's method is going to converge a lot faster than finding the cycles just by iterating a single point (as is how bifurcations diagrams are usually made) under fc itself. Milo Brandt[ 4]
方法
首先,让我们找出经过一次应用 f {\displaystyle f} f c ( z ) = z {\displaystyle f_{c}(z)=z}
z 2 + c = z , {\displaystyle z^{2}+c=z,\,} 可以改写为:
z 2 − z + c = 0. {\displaystyle \ z^{2}-z+c=0.} 由于这是一个关于单个未知数的一般 二次方程 ,我们可以应用 标准二次方程求解公式
α 1 = 1 − 1 − 4 c 2 {\displaystyle \alpha _{1}={\frac {1-{\sqrt {1-4c}}}{2}}} α 2 = 1 + 1 − 4 c 2 . {\displaystyle \alpha _{2}={\frac {1+{\sqrt {1-4c}}}{2}}.} 因此,对于 c ∈ C ∖ { 1 / 4 } {\displaystyle c\in \mathbb {C} \setminus \{1/4\}} α 1 {\displaystyle \alpha _{1}} α 2 {\displaystyle \alpha _{2}}
由于
α 1 = 1 2 − m {\displaystyle \alpha _{1}={\frac {1}{2}}-m} α 2 = 1 2 + m {\displaystyle \alpha _{2}={\frac {1}{2}}+m} m = 1 − 4 c 2 , {\displaystyle m={\frac {\sqrt {1-4c}}{2}},} 我们有 α 1 + α 2 = 1 {\displaystyle \alpha _{1}+\alpha _{2}=1}
因此,不动点关于 z = 1 / 2 {\displaystyle z=1/2}
此图显示了不动点(均为排斥不动点)。 沿水平轴的 c 的不动点 F(z ) = z *z 的 Fatou 集 ,并标出了不动点 这里通常使用不同的符号:[ 5]
α c = 1 − 1 − 4 c 2 {\displaystyle \alpha _{c}={\frac {1-{\sqrt {1-4c}}}{2}}} λ α c = 1 − 1 − 4 c {\displaystyle \lambda _{\alpha _{c}}=1-{\sqrt {1-4c}}} 以及
β c = 1 + 1 − 4 c 2 {\displaystyle \beta _{c}={\frac {1+{\sqrt {1-4c}}}{2}}} λ β c = 1 + 1 − 4 c . {\displaystyle \lambda _{\beta _{c}}=1+{\sqrt {1-4c}}.} 我们再次得到
α c + β c = 1. {\displaystyle \alpha _{c}+\beta _{c}=1.} 不动点之间的距离
1 − Δ 2 < 1 2 < 1 + Δ 2 {\displaystyle {\frac {1-\Delta }{2}}<{\frac {1}{2}}<{\frac {1+\Delta }{2}}} 是 delta Δ {\displaystyle \Delta }
其中
Δ = 1 − 4 c {\displaystyle \Delta ={\sqrt {1-4c}}} 对于 c = 1 4 {\displaystyle c={\frac {1}{4}}} Δ ( 1 4 ) = 0 = 0 {\displaystyle \Delta ({\frac {1}{4}})={\sqrt {0}}=0}
对于 c = 0 {\displaystyle c=0} Δ ( 1 ) = 1 = 1 {\displaystyle \Delta (1)={\sqrt {1}}=1}
由于 关于 *z* 的导数 为
P c ′ ( z ) = d d z P c ( z ) = 2 z , {\displaystyle P_{c}'(z)={\frac {d}{dz}}P_{c}(z)=2z,} 我们有
P c ′ ( α c ) + P c ′ ( β c ) = 2 α c + 2 β c = 2 ( α c + β c ) = 2. {\displaystyle P_{c}'(\alpha _{c})+P_{c}'(\beta _{c})=2\alpha _{c}+2\beta _{c}=2(\alpha _{c}+\beta _{c})=2.} 这意味着 P c {\displaystyle P_{c}}
这些点通过以下事实来区分
β c {\displaystyle \beta _{c}} 角度为 0 时,外部射线 的着陆点,其中 c ∈ M ∖ { 1 / 4 } {\displaystyle c\in M\setminus \left\{1/4\right\}}
Julia 集的最排斥不动点。
位于右侧(当不动点在实轴 上不对称时),它是连接 Julia 集的最右端点(除花椰菜外)。[ 6] α c {\displaystyle \alpha _{c}} 几条射线的着陆点。
当 c {\displaystyle c}
在 Mandelbrot 集的肢体根点是抛物线的。
对于 c {\displaystyle c} 特殊情况
二次映射的一个重要情况是 c = 0 {\displaystyle c=0} α 1 = 0 {\displaystyle \alpha _{1}=0} α 2 = 1 {\displaystyle \alpha _{2}=1} 不动点 ,而 1 属于Julia 集 。
只有一个不动点
我们有 α 1 = α 2 {\displaystyle \alpha _{1}=\alpha _{2}} 1 − 4 c = 0. {\displaystyle 1-4c=0.} c = 1 / 4 , {\displaystyle c=1/4,} α 1 = α 2 = 1 / 2 {\displaystyle \alpha _{1}=\alpha _{2}=1/2} c = 1 / 4 {\displaystyle c=1/4} 实 值。
我们可以通过添加无穷大 将复平面 C {\displaystyle \mathbb {C} } 黎曼球面(扩展复平面) C ^ {\displaystyle \mathbb {\hat {C}} }
C ^ = C ∪ { ∞ } {\displaystyle \mathbb {\hat {C}} =\mathbb {C} \cup \{\infty \}} 并扩展 f c {\displaystyle f_{c}} f c ( ∞ ) = ∞ . {\displaystyle f_{c}(\infty )=\infty .}
那么无穷大 是
超吸引
f c {\displaystyle f_{c}} [ 7] f c ( ∞ ) = ∞ = f c − 1 ( ∞ ) . {\displaystyle f_{c}(\infty )=\infty =f_{c}^{-1}(\infty ).} 从周期 1 到 2 的分岔 复二次映射 fc(z)=z*z +c 中周期点从周期 1 到 2 的分岔 2 周期循环是两个不同的点 β 1 {\displaystyle \beta _{1}} β 2 {\displaystyle \beta _{2}} f c ( β 1 ) = β 2 {\displaystyle f_{c}(\beta _{1})=\beta _{2}} f c ( β 2 ) = β 1 {\displaystyle f_{c}(\beta _{2})=\beta _{1}}
f c ( f c ( β n ) ) = β n {\displaystyle f_{c}(f_{c}(\beta _{n}))=\beta _{n}} 对于 n ∈ { 1 , 2 } {\displaystyle n\in \{1,2\}}
f c ( f c ( z ) ) = ( z 2 + c ) 2 + c = z 4 + 2 c z 2 + c 2 + c . {\displaystyle f_{c}(f_{c}(z))=(z^{2}+c)^{2}+c=z^{4}+2cz^{2}+c^{2}+c.} 将此等式设置为z ,我们得到
z 4 + 2 c z 2 − z + c 2 + c = 0. {\displaystyle z^{4}+2cz^{2}-z+c^{2}+c=0.} 此方程是 4 次多项式,因此有四个(可能不不同的)解。但是,我们已经知道两个解。它们是 α 1 {\displaystyle \alpha _{1}} α 2 {\displaystyle \alpha _{2}} f {\displaystyle f} f {\displaystyle f}
因此,我们的 4 次多项式可以用两种方式分解
( z − α 1 ) ( z − α 2 ) ( z − β 1 ) ( z − β 2 ) = 0. {\displaystyle (z-\alpha _{1})(z-\alpha _{2})(z-\beta _{1})(z-\beta _{2})=0.\,} 这直接扩展为 x 4 − A x 3 + B x 2 − C x + D = 0 {\displaystyle x^{4}-Ax^{3}+Bx^{2}-Cx+D=0}
D = α 1 α 2 β 1 β 2 , {\displaystyle D=\alpha _{1}\alpha _{2}\beta _{1}\beta _{2},\,} C = α 1 α 2 β 1 + α 1 α 2 β 2 + α 1 β 1 β 2 + α 2 β 1 β 2 , {\displaystyle C=\alpha _{1}\alpha _{2}\beta _{1}+\alpha _{1}\alpha _{2}\beta _{2}+\alpha _{1}\beta _{1}\beta _{2}+\alpha _{2}\beta _{1}\beta _{2},\,} B = α 1 α 2 + α 1 β 1 + α 1 β 2 + α 2 β 1 + α 2 β 2 + β 1 β 2 , {\displaystyle B=\alpha _{1}\alpha _{2}+\alpha _{1}\beta _{1}+\alpha _{1}\beta _{2}+\alpha _{2}\beta _{1}+\alpha _{2}\beta _{2}+\beta _{1}\beta _{2},\,} A = α 1 + α 2 + β 1 + β 2 . {\displaystyle A=\alpha _{1}+\alpha _{2}+\beta _{1}+\beta _{2}.\,} 我们已经有两个解,只需要另外两个。因此问题相当于求解一个二次多项式。特别注意,
α 1 + α 2 = 1 − 1 − 4 c 2 + 1 + 1 − 4 c 2 = 1 + 1 2 = 1 {\displaystyle \alpha _{1}+\alpha _{2}={\frac {1-{\sqrt {1-4c}}}{2}}+{\frac {1+{\sqrt {1-4c}}}{2}}={\frac {1+1}{2}}=1} 以及
α 1 α 2 = ( 1 − 1 − 4 c ) ( 1 + 1 − 4 c ) 4 = 1 2 − ( 1 − 4 c ) 2 4 = 1 − 1 + 4 c 4 = 4 c 4 = c . {\displaystyle \alpha _{1}\alpha _{2}={\frac {(1-{\sqrt {1-4c}})(1+{\sqrt {1-4c}})}{4}}={\frac {1^{2}-({\sqrt {1-4c}})^{2}}{4}}={\frac {1-1+4c}{4}}={\frac {4c}{4}}=c.} 将这些加到上面,我们得到 D = c β 1 β 2 {\displaystyle D=c\beta _{1}\beta _{2}} A = 1 + β 1 + β 2 {\displaystyle A=1+\beta _{1}+\beta _{2}} f {\displaystyle f}
D = c β 1 β 2 = c 2 + c {\displaystyle D=c\beta _{1}\beta _{2}=c^{2}+c} A = 1 + β 1 + β 2 = 0. {\displaystyle A=1+\beta _{1}+\beta _{2}=0.} 由此,我们很容易得到
β 1 β 2 = c + 1 {\displaystyle \beta _{1}\beta _{2}=c+1} β 1 + β 2 = − 1 {\displaystyle \beta _{1}+\beta _{2}=-1} 从这里,我们构造一个以 A ′ = 1 , B = 1 , C = c + 1 {\displaystyle A'=1,B=1,C=c+1}
β 1 = − 1 − − 3 − 4 c 2 {\displaystyle \beta _{1}={\frac {-1-{\sqrt {-3-4c}}}{2}}} β 2 = − 1 + − 3 − 4 c 2 . {\displaystyle \beta _{2}={\frac {-1+{\sqrt {-3-4c}}}{2}}.} 仔细观察表明
f c ( β 1 ) = β 2 {\displaystyle f_{c}(\beta _{1})=\beta _{2}} f c ( β 2 ) = β 1 , {\displaystyle f_{c}(\beta _{2})=\beta _{1},} 这意味着这两个点是单个周期为 2 的循环上的两个点。
我们可以使用 多项式长除法 将因子 ( z − α 1 ) {\displaystyle (z-\alpha _{1})} ( z − α 2 ) , {\displaystyle (z-\alpha _{2}),} α 1 {\displaystyle \alpha _{1}} α 2 {\displaystyle \alpha _{2}}
( z 2 + c ) 2 + c − z = ( z 2 + c − z ) ( z 2 + z + c + 1 ) . {\displaystyle (z^{2}+c)^{2}+c-z=(z^{2}+c-z)(z^{2}+z+c+1).\,} 第一个因式的根是两个不动点。它们在主心形之外是排斥的。
第二个因式有两个根
− 1 ± − 3 − 4 c 2 . {\displaystyle {\frac {-1\pm {\sqrt {-3-4c}}}{2}}.\,} 这两个根,与第一种方法找到的相同,形成了周期为 2 的轨道。[ 8]
再次,让我们看看 c = 0 {\displaystyle c=0}
β 1 = − 1 − i 3 2 {\displaystyle \beta _{1}={\frac {-1-i{\sqrt {3}}}{2}}} β 2 = − 1 + i 3 2 , {\displaystyle \beta _{2}={\frac {-1+i{\sqrt {3}}}{2}},} 它们都是复数。我们有 | β 1 | = | β 2 | = 1 {\displaystyle |\beta _{1}|=|\beta _{2}|=1} c = − 1 {\displaystyle c=-1} β 1 = 0 {\displaystyle \beta _{1}=0} β 2 = − 1 {\displaystyle \beta _{2}=-1}
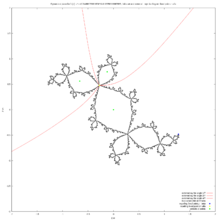
f (z ) = z *z −0.75 的周期为 6 的周期点作为 2 个隐式曲线的交点方程 f ( n ) ( z ) = z {\displaystyle f^{(n)}(z)=z} n
不存在 五次或更高次的多项式方程的 根式解 ,因此,一般情况下,周期大于 2 的循环上的点必须使用 数值方法 计算。但是,在周期为 4 的特定情况下,循环点具有根式解的冗长表达式。[ 9]
当 c = –2 时,所有周期的周期点都存在三角函数解。情况 z n + 1 = z n 2 − 2 {\displaystyle z_{n+1}=z_{n}^{2}-2} 逻辑斯谛映射 情况 r = 4: x n + 1 = 4 x n ( 1 − x n ) . {\displaystyle x_{n+1}=4x_{n}(1-x_{n}).} z = 2 − 4 x . {\displaystyle z=2-4x.} x 的 k 循环之一(所有循环都是排斥的)是
sin 2 ( 2 π 2 k − 1 ) , sin 2 ( 2 ⋅ 2 π 2 k − 1 ) , sin 2 ( 2 2 ⋅ 2 π 2 k − 1 ) , sin 2 ( 2 3 ⋅ 2 π 2 k − 1 ) , … , sin 2 ( 2 k − 1 2 π 2 k − 1 ) . {\displaystyle \sin ^{2}\left({\frac {2\pi }{2^{k}-1}}\right),\,\sin ^{2}\left(2\cdot {\frac {2\pi }{2^{k}-1}}\right),\,\sin ^{2}\left(2^{2}\cdot {\frac {2\pi }{2^{k}-1}}\right),\,\sin ^{2}\left(2^{3}\cdot {\frac {2\pi }{2^{k}-1}}\right),\dots ,\sin ^{2}\left(2^{k-1}{\frac {2\pi }{2^{k}-1}}\right).}
为了创建曼德布罗集的周期性分量,对于 f c ( z ) = z 2 + c {\displaystyle f_{c}(z)=z^{2}+c}
从 z 0 := 0 {\displaystyle z_{0}:=0} m := ∞ {\displaystyle m:=\infty }
对于每个 n = 1 , 2 , 3 , . . . {\displaystyle n=1,2,3,...}
计算 z n := f c ( z n − 1 ) {\displaystyle z_{n}:=f_{c}(z_{n-1})}
如果 | z n | < m {\displaystyle |z_{n}|<m} 设置 m := | z n | {\displaystyle m:=|z_{n}|}
使用 牛顿法 求解 w = f c ∘ n ( w ) {\displaystyle w=f_{c}^{\circ n}(w)} w ( 0 ) := z n {\displaystyle w^{(0)}:=z_{n}} n {\displaystyle n} w ( i + 1 ) := w ( i ) − f c ∘ n ( w ( i ) ) − w ( i ) f c ∘ n ′ ( w ( i ) ) − 1 {\displaystyle w^{(i+1)}:=w^{(i)}-{\frac {f_{c}^{\circ n}(w^{(i)})-w^{(i)}}{{f_{c}^{\circ n}}'(w^{(i)})-1}}}
计算循环的导数 λ := f c ∘ n ′ ( w ) {\displaystyle \lambda :={f_{c}^{\circ n}}'(w)}
如果 | λ | < 1 {\displaystyle |\lambda |<1} c {\displaystyle c} n {\displaystyle n}
λ {\displaystyle \lambda } w {\displaystyle w} n {\displaystyle n} 使用牛顿法是为了加速计算 w {\displaystyle w} f c {\displaystyle f_{c}} w {\displaystyle w} λ {\displaystyle \lambda } 1 {\displaystyle 1}
我没有关于正确性的完整证明(但这并不意味着我认为它是错误的;这些图像看起来合理)。它依赖于围绕给定周期的每个双曲分量的“原子域”。
它还依赖于牛顿法得到的循环与迭代得到的极限循环相同:这对于二次曼德布罗特集是正确的,因为它只有一个有限的临界点, 0 {\displaystyle 0} ∞ {\displaystyle \infty } https://math.stackexchange.com/a/3952801 >),这意味着最多只能有一个吸引或抛物线循环。
有关 C99 实现,请参见我的博客文章 <https://mathr.co.uk/blog/2014-11-02_practical_interior_distance_rendering.html >
心形/球体检查
int GivePeriod ( complex double c ){
if ( cabs2 ( c ) > 4.0 ) { return 0 ;} // exterior : out of first lemniscte
if ( cabs2 ( 1.0 - csqrt ( 1.0-4.0 * c )) <= 1.0 ) { return 1 ;} // main cardioid
if ( cabs2 ( 4.0 * c + 4 ) <= 1.0 ){ return 2 ;} // period 2 component
int period = GivePeriodByIteration ( c );
if ( period < 0 ) // last chance
{
iUnknownPeriod += 1 ;
//period = m_d_box_period_do(c, 0.5, iterMax_LastIteration); // not working good
}
// period > 0 means is periodic
// period = 0 means is not periodic = exterior = escaping to infinity
// period < 0 means period not found, maybe increase global variable iterMax_Period ( see local_setup)
return period ;
}