部分

克劳德·海兰德-艾伦为基于 CPU 的曼德勃罗集可视化设计的库和 c 程序^[1]
用于 Haskell 的 mandelbrot-prelude 库（终端中低分辨率图像，使用块图形字符）

安装

依赖项

共享库

ldd m-render
	linux-vdso.so.1 =>  (0x00007ffcae4e7000)
	libmandelbrot-graphics.so => /home/a/opt/lib/libmandelbrot-graphics.so (0x00007fb8f9a12000)
	libcairo.so.2 => /usr/lib/x86_64-linux-gnu/libcairo.so.2 (0x00007fb8f96df000)
	libmandelbrot-numerics.so => /home/a/opt/lib/libmandelbrot-numerics.so (0x00007fb8f94cf000)
	libpthread.so.0 => /lib/x86_64-linux-gnu/libpthread.so.0 (0x00007fb8f92b2000)
	libc.so.6 => /lib/x86_64-linux-gnu/libc.so.6 (0x00007fb8f8ee9000)
	libm.so.6 => /lib/x86_64-linux-gnu/libm.so.6 (0x00007fb8f8bdf000)
	libgomp.so.1 => /usr/lib/x86_64-linux-gnu/libgomp.so.1 (0x00007fb8f89bd000)
	libpixman-1.so.0 => /usr/lib/x86_64-linux-gnu/libpixman-1.so.0 (0x00007fb8f8715000)
	libfontconfig.so.1 => /usr/lib/x86_64-linux-gnu/libfontconfig.so.1 (0x00007fb8f84d1000)
	libfreetype.so.6 => /usr/lib/x86_64-linux-gnu/libfreetype.so.6 (0x00007fb8f8227000)
	libpng12.so.0 => /lib/x86_64-linux-gnu/libpng12.so.0 (0x00007fb8f8002000)
	libxcb-shm.so.0 => /usr/lib/x86_64-linux-gnu/libxcb-shm.so.0 (0x00007fb8f7dfd000)
	libxcb-render.so.0 => /usr/lib/x86_64-linux-gnu/libxcb-render.so.0 (0x00007fb8f7bf3000)
	libxcb.so.1 => /usr/lib/x86_64-linux-gnu/libxcb.so.1 (0x00007fb8f79d1000)
	libXrender.so.1 => /usr/lib/x86_64-linux-gnu/libXrender.so.1 (0x00007fb8f77c6000)
	libX11.so.6 => /usr/lib/x86_64-linux-gnu/libX11.so.6 (0x00007fb8f748c000)
	libXext.so.6 => /usr/lib/x86_64-linux-gnu/libXext.so.6 (0x00007fb8f727a000)
	libz.so.1 => /lib/x86_64-linux-gnu/libz.so.1 (0x00007fb8f705f000)
	librt.so.1 => /lib/x86_64-linux-gnu/librt.so.1 (0x00007fb8f6e57000)
	libmpc.so.3 => /usr/local/lib/libmpc.so.3 (0x00007fb8f6c3e000)
	libmpfr.so.4 => /usr/local/lib/libmpfr.so.4 (0x00007fb8f69db000)
	libgmp.so.10 => /usr/local/lib/libgmp.so.10 (0x00007fb8f6764000)
	/lib64/ld-linux-x86-64.so.2 (0x0000564eca780000)
	libdl.so.2 => /lib/x86_64-linux-gnu/libdl.so.2 (0x00007fb8f6560000)
	libexpat.so.1 => /lib/x86_64-linux-gnu/libexpat.so.1 (0x00007fb8f6336000)
	libXau.so.6 => /usr/lib/x86_64-linux-gnu/libXau.so.6 (0x00007fb8f6132000)
	libXdmcp.so.6 => /usr/lib/x86_64-linux-gnu/libXdmcp.so.6 (0x00007fb8f5f2b000)

objdump -p m-render | grep NEEDED
  NEEDED               libmandelbrot-graphics.so
  NEEDED               libcairo.so.2
  NEEDED               libmandelbrot-numerics.so
  NEEDED               libpthread.so.0
  NEEDED               libc.so.6

objdump -p m-stretching-cusps | grep NEEDED
  NEEDED               libmandelbrot-graphics.so
  NEEDED               libcairo.so.2
  NEEDED               libmandelbrot-numerics.so
  NEEDED               libm.so.6
  NEEDED               libgmp.so.10
  NEEDED               libpthread.so.0
  NEEDED               libc.so.6

git

git clone https://code.mathr.co.uk/mandelbrot-graphics.git

以及包含 mandelbrot-graphics 的目录中

 make -C mandelbrot-graphics/c/lib prefix=${HOME}/opt install
 make -C mandelbrot-graphics/c/bin prefix=${HOME}/opt install

然后运行

 export LD_LIBRARY_PATH=${HOME}/opt/lib

检查

echo $LD_LIBRARY_PATH

结果

 /home/a/opt/lib

或者

 export PATH=${HOME}/opt/bin:${PATH}

检查

    echo $PATH

要永久设置它，更改文件

.profile^[2]
/etc/ld.so.conf.d/*.conf^[3]

更新

git

从 mandelbrot-graphics 目录中打开的控制台中

 git pull

如果你进行了一些本地更改，你可以撤销它们

 git checkout -f

然后

 git pull

现在重新安装

重新编译新版本

bash 脚本

#!/bin/bash
cd ~
make -C mandelbrot-graphics/c/lib prefix=${HOME}/opt install
make -C mandelbrot-graphics/c/bin prefix=${HOME}/opt install
export LD_LIBRARY_PATH=${HOME}/opt/lib 
export PATH=${HOME}/opt/bin:${PATH}
cd /home/a/mandelbrot-graphics/c/bin

名称

m

前缀 m 来自 Mandelbrot

r/d

名称中的前缀 r 或 d 描述精度

d = 双精度
r = 任意精度

示例

 m_d_attractor(double _Complex *z_out, double _Complex z_guess, double _Complex c, int period, int maxsteps)
 m_r_attractor(mpc_t z_out, const mpc_t z_guess, const mpc_t c, int period, int maxsteps)

如何使用它？

序言

Haskell 程序

let c = nucleus 100 . (!! (8 * 2 * 100)) . exRayIn 8 . fromQ . fst . addressAngles . pAddress $ "1 7/12 5/9 100" ; r = 2 * magnitude (size 100 c) in putImage c r 10000

它提供

终端中低分辨率图像，使用块图形字符
中心、大小和迭代次数

-0.5664388911664133 + -0.4792791697756855 i @ 2.810e-8 (10000 iterations)

lib 目录中的过程

C 源代码应该*只*包含 #include <mandelbrot-numerics.h>
使用 pkg-config 编译和链接：参见 mandelbrot-numerics/c/bin/Makefile 作为示例
开始的最快方法是将你的文件放在 mandelbrot-numerics/c/bin 中，然后运行 make

m_d_transform_rectangular

 m_d_transform *rect = m_d_transform_rectangular(w, h, c, r); //

其中

w = 宽度（以像素为单位）
h = 高度（以像素为单位）
c = 图像的中心（复数）
r = 图像的半径（双精度数）

m_d_interior

找到曼德勃罗集的点 c，给定特定的双曲分量和所需的内部角度。它涉及在两个复变量中使用牛顿法来解决^[4]

${\begin{cases}F^{p}(z,c)=z\\{\partial \over \partial z}F^{p}(z,c)=b\end{cases}}$

其中

$F^{0}(z,c)=z$
$F^{q+1}(z,c)=F^{q}(F(z,c)^{2}+c)$
p 是目标分量的周期
$\theta$ 是所需的内部角度
r 是内部半径 $r\leq 1$ 。当 r = 1.0 时，点在边界上。当 r = 0 时，点位于分量中心（= 核心）
$b=re^{2\pi i\theta }$ 是点 c 的乘数

双曲线分量由以下描述

周期
核心

语法

 extern m_newton m_d_interior(double _Complex *z_out, double _Complex *c_out, double _Complex z_guess, double _Complex c_guess, double _Complex interior, int period, int maxsteps)

输入

z_guess
c_guess（通常是选定双曲线分量的核心）
interior（乘数）
周期
maxstep

输出

c 是点的坐标（c_out）
z 是周期点（z_out）
result（m_newton）描述牛顿算法如何结束：m_failed、m_stepped、m_converged。它在 ~/mandelbrot-numerics/c/include/mandelbrot-numerics.h 中定义

使用示例

 m_d_interior(&z, &half, nucleus, nucleus, -1, period, 64);
 m_d_interior(&z, &cusp, nucleus, nucleus, 1, period, 64);
 m_d_interior(&z, &third2, -1, -1, cexp(I * twopi / 3), 2, 64);

bin 目录中的程序

列表

~/mandelbrot-graphics/c/bin$ ls -1a *.c

结果

m-cardioid-warping.c   
m-render.c             
m-subwake-diagram-b.c
m-dense-misiurewicz.c  
m-stretching-cusps.c   
m-subwake-diagram-c.c
m-feigenbaum-zoom.c    
m-subwake-diagram-a.c

m-warped-midgets

./m-warped-midgets

结果

     4 -1.565201668337550256e-01 + 1.032247108922831780e+00 i @ 1.697e-02
     8 4.048996651751222142e-01 + 1.458203637665893004e-01 i @ 2.743e-03
    16 2.925037532341934199e-01 + 1.492506899834379792e-02 i @ 3.484e-04
    32 2.602618199285007261e-01 + 1.667791320926505921e-03 i @ 4.113e-05
    64 2.524934589775105209e-01 + 1.971526796077277045e-04 i @ 4.920e-06
   128 2.506132008410751344e-01 + 2.396932642510365294e-05 i @ 5.997e-07
   256 2.501519680089798192e-01 + 2.954962325906873815e-06 i @ 7.398e-08
   512 2.500378219137852631e-01 + 3.668242052764783887e-07 i @ 9.185e-09
  1024 2.500094340031833728e-01 + 4.569478652064606379e-08 i @ 1.144e-09
  2048 2.500023558032561377e-01 + 5.701985912706822671e-09 i @ 1.428e-10
  4096 2.500005886128087162e-01 + 7.121326948562671441e-10 i @ 1.783e-11
  8192 2.500001471109009610e-01 + 8.897814201389663379e-11 i @ 2.228e-12

周期性扫描

周期性扫描^[5]：用曼德布罗集分量的周期标记参数平面的图片可以提供对其更深层结构的洞察。

文件：m-period.scan.c

运行控制台程序

./m-period-scan

usage: ./m-period-scan out.png width height creal cimag radius maxiters mingridsize minfontsize maxfontsize maxatoms periodmod periodneq

示例

./m-period-scan out1.png 1500	1000 0.0	0.0 1.5  10000   100 	0.1	30.0     100  3 1

莫比乌斯

莫比乌斯变换

./moebius
find point c of component with period = 2 	 multiplier = -0.4999999999999998+0.8660254037844387	 located near c=  -1.0000000000000000+0.0000000000000000
find point c of component with period = 4 	 multiplier = -1.0000000000000000+0.0000000000000000	 located near c=  -1.3107026413368328+0.0000000000000000
find point c of component with period = 4 	 multiplier = -0.4999999999999998+0.8660254037844387	 located near c=  -1.3107026413368328+0.0000000000000000
find point c of component with period = 8 	 multiplier = -1.0000000000000000+0.0000000000000000	 located near c=  -1.3815474844320617+0.0000000000000000
find point c of component with period = 8 	 multiplier = -0.4999999999999998+0.8660254037844387	 located near c=  -1.3815474844320617+0.0000000000000000
find point c of component with period = 2 	 multiplier = -0.5000000000000004-0.8660254037844384	 located near c=  -1.0000000000000000+0.0000000000000000
find point c of component with period = 2 	 multiplier = -0.8090169943749476-0.5877852522924730	 located near c=  -1.0000000000000000+0.0000000000000000
find point c of component with period = 2 	 multiplier = -0.7071067811865477-0.7071067811865475	 located near c=  -1.0000000000000000+0.0000000000000000
find point c of component with period = 2 	 multiplier = -0.6548607339452852-0.7557495743542582	 located near c=  -1.0000000000000000+0.0000000000000000
find point c of component with period = 3 	 multiplier = -1.0000000000000000+0.0000000000000000	 located near c=  -1.7548776662466927+0.0000000000000000
find point c of component with period = 3 	 multiplier = 1.0000000000000000+0.0000000000000000	 located near c=  -1.7548776662466927+0.0000000000000000
find point c of component with period = 6 	 multiplier = -1.0000000000000000+0.0000000000000000	 located near c=  -1.7728929033816239+0.0000000000000000
find point c of component with period = 6 	 multiplier = -0.4999999999999998+0.8660254037844387	 located near c=  -1.7728929033816239+0.0000000000000000
find point c of component with period = 12 	 multiplier = -1.0000000000000000+0.0000000000000000	 located near c=  -1.7782668211110817+0.0000000000000000
find point c of component with period = 12 	 multiplier = -0.4999999999999998+0.8660254037844387	 located near c=  -1.7782668211110817+0.0000000000000000

m-furcation-rainbow

  For non-real C you can plot all the limit-cycle Z on one image, chances of overlap are small.  You can colour according to the position along the path.  
  In attached I have coloured using hue red at roots, going through yellow towards the next bond point in a straight line through the   interior coordinate space (interior coordinate is derivative of limit cycle).  
  I have just plotted points, so there are gaps.  Perhaps it could be improved by drawing line segments between Z values, but I'm not 100% sure if the first Z value found will always correspond to the same logical line, 
  and keeping track of a changing number of "previous Z" values isn't too fun either. Claude^[6]

运行

 /m-furcation-rainbow 13.png  "1/3" "1/3" "1/3"

m-dense-misiurewicz

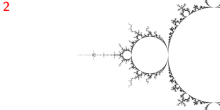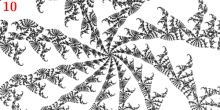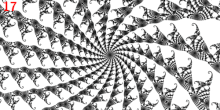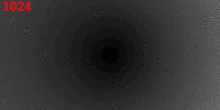
该程序基于 mandelbrot-graphics 中的 m-render.c。

它绘制一系列 png 图像

m-island-zoom

m-island-zoom

制作 150 张 png 图像，显示缩放至 3 个岛屿（尾流中最大的岛屿）

一个位于主天线（周期 3）上，中心 c = -1.754877666246693 +0.000000000000000 i，位于 1/2 尾流中
周期 4，中心 c = -0.156520166833755 +1.032247108922832 i，位于 1/3 尾流中
周期 5，地址为 1-> 2-(1/3)-> 6，中心 c = -1.256367930068181 +0.380320963472722 i

心形变形

曼德布罗集心形外部被变形以呈现旋转的外观。

变换由较小的组件组成，包括

心形映射到圆
圆到直线的莫比乌斯变换
线性平移（动画化）
线性平移的逆
圆到直线的莫比乌斯变换的逆

这些变换及其导数（用于距离估计着色）在此处描述：https://mathr.co.uk/blog/2013-12-16_stretching_cusps.html

用于渲染动画的程序是在 C 中使用此处找到的 mandelbrot-graphics 库实现的：https://code.mathr.co.uk/mandelbrot-graphics 该程序位于存储库中，为 c/bin/m-cardioid/warping.c https://code.mathr.co.uk/mandelbrot-graphics/blob/60adc5ab8f14aab1be479469dfcf5ad3469feea0:/c/bin/m-cardioid-warping.c

x 和内角之间有什么关系？

毛发

m-stretching-cusps

曼德布罗集主心形的展开

可以添加使用说明

if (! (argc == 7)) {
    printf("no input \n");
    printf("example usage :  \n");
    printf("%s re(nucleus) im(nucleus) period t_zero t_one t_infinity  \n", argv[0] );
    printf("%s 0 0 1 1/2 1/3 0  \n", argv[0] );
    return 1;
  }

示例用法

 m-stretching-cusps 0 0 1 1/2 1/3 0

输入

父分量
- re(核心)
- im(核心)
- 周期
3 个子分量的内角
- t0
- t1
- tinfinity

测试结果

 P0 = -7.5000000000000000e-01 1.2246467991473532e-16
 P1 = -1.2499999999999981e-01 6.4951905283832900e-01
 Pinf = 2.5000000000000000e-01 0.0000000000000000e+00

和图像 out.png

duble r = 0.5; // proportional to the number of components on the strip, 
 /*
  r = 0.5 gives 4 prominent components counted from period 1 to one side only 
  r = 1.0 gives 10 components
  r = 1.5 gives 15
  r = 2.0 gives 20 ( one can see 2 sides of cardioid ?? because it is near cusp)
  r = 2.5 gives 26
  r = 5.0 gives 50

它使用

行列式（来自 mandelbrot-numerics 库的 m_d_mat2）用于计算莫比乌斯变换的系数 a、b、c、d^[7]
由 3 个点定义的莫比乌斯变换的 m_d_transform_moebius3 函数

m-stretching-cusps 0 0 1 1/2 1/3 0
parent component with period = 1 and nucleus = 0.0000000000000000e+00 0.0000000000000000e+00
child component with with internal angle tzero = 1/2 and nucleus c = zero = -7.5000000000000000e-01 1.2246467991473532e-16  
child component with with internal angle tone = 1/3 and nucleus c = one = -1.2499999999999981e-01 6.4951905283832900e-01
child component with with internal angle tinfinity = 0 and nucleus c = infinity = 2.5000000000000000e-01 0.0000000000000000e+00
Moebius coefficients
	a = -0.5000000000000002 ; -0.8660254037844387
	b = 1.4999999999999998 ; -0.8660254037844390
	c = 0.5000000000000002 ; 0.8660254037844387
	d = 1.4999999999999998 ; -0.8660254037844388

image 1_0.500000.png saved
filename = period_r

m-misiurewicz-basins

m-misiurewicz-basins
usage: m-misiurewicz-basins out.png width height creal cimag radius maxiters preperiod period

m-render

它是其他程序的基础程序。

这段代码片段描述了如何使用它

int main(int argc, char **argv) {
  if (argc != 8) {
    fprintf(stderr, "usage: %s out.png width height creal cimag radius maxiters\n", argv[0]);
    return 1;
  }

示例

  m-render a.png 1000 1000  -0.75  0 1.5 10000

结果是使用 DEM 的曼德布罗集边界

m-render 1995.png 7680 4320 -0.5664388911664133 -0.4792791697756855 3e-8 10000 1

m-streching-feigenbaum.c

费根鲍姆拉伸，带有外部射线（周期倍增级联）

m-subwake-diagram-a

m-subwake-diagram-b

m-subwake-diagram-c

参见

词典

参考文献

[1] rot-graphics - 由 Claude Heiland-Allen 编写的基于 CPU 的 Mandelbrot 集可视化程序

[2] stackoverflow 问题：如何在 Linux 上永久设置路径

[3] ubuntu 环境变量

[4] Mandelbrot 集中的内部坐标，作者：Claude Heiland-Allen

[5] 周期性扫描，作者：Claude Heiland-Allen

[6] ractalforums.org : 三叉分岔及更多

[7] 维基百科中关于莫比乌斯变换的显式行列式公式

[1]

[2]

[3]

[4]

[5]

[6]

[7]