交通基础/水平曲线

水平曲线 是公路几何设计中两个重要的过渡元素之一（另一个是竖曲线）。水平曲线提供两段直线型路段之间的过渡，允许车辆以逐渐的速率而不是急转弯的方式完成转弯。曲线的設計依賴于道路的預期設計速度，以及其他因素，包括排水和摩擦力。这些曲线是半圆形，以提供驾驶员恒定的转弯速率，其半径由围绕向心力的物理定律确定。

水平曲线的基本特性

物理特性

挪威奥斯陆的水平曲线

除了动量之外，当车辆转弯时，还有两种力作用于它。第一种是重力，它将车辆拉向地面。第二种是离心力，而它的反作用力，即向心加速度，则需要使车辆保持在弯曲的路径上。对于任何给定的速度，对于更紧的转弯（半径较小）比更宽的转弯（半径较大），向心力需要更大。在水平表面上，侧向摩擦力 $f_{s}$ 作为对抗离心力的力量，但它通常提供非常少的阻力/力量。因此，车辆必须在水平面上画一个非常大的圆才能转弯。

鉴于道路设计通常受限于非常狭窄的设计区域，因此通常不鼓励进行宽转弯。为了解决这个问题，水平曲线的設計師會將道路傾斜一定的角度。这种倾斜被称为超高，或 $e$，即在给定一定行程的情况下，道路横截面角度的上升量，也称为坡度。超高在弯道上的存在使得一部分向心力可以由地面抵消，从而允许车辆以比平坦表面上允许的更快的速度完成转弯。超高在降雨事件中也起到另一个重要作用，它有助于排水，因为水流过道路而不是积聚在道路上。通常，超高限制在 14% 以下，因为工程师需要考虑弯道上停放的车辆，因为那里不存在向心力。

水平曲线的允许半径 $R$ 可以通过知道预期的设计速度 $V$、摩擦系数和弯道上的允许超高来确定。

$R={\frac {v^{2}}{g\left({e+f_{s}}\right)}}\,\!$

有了这个半径，从业人员就可以确定曲线的度数，以查看它是否在可接受的标准范围内。曲线的度数，$D_{a}$，可以通过以下公式计算，该公式以公制给出。

$\%R={\frac {1746}{D_{a}}}\%\,\!$

其中

• $D_{a}\,\!$= 曲线的度数 [30.5 米 (100 英尺) 弧线在水平曲线上的张角

超高应用

布里斯托尔赛车场

你会看到一个地方是汽车赛车场，那里有陡峭的倾斜。这些赛道不在冬季运营，因此可以避免冬季天气带来的倾斜问题。司机也特别熟练，不过事故并不少见。对于 NASCAR 粉丝来说，以下表格可能会有所帮助。

表：美国赛道上的倾斜

赛道	长度（英里）	倾斜（度）
芝加哥汽车赛车场	1	0.00
英菲尼昂赛车场	1.949
沃特金斯格伦国际赛道	2.45
波科诺赛车场	2.5	6.00
迈阿密-霍姆斯特德赛车场	1.5	8.00
印第安纳波利斯赛车场	2.5	9.00
孟菲斯赛车场	0.75	11.00
凤凰国际赛车场	1	11.00
拉斯维加斯赛车场	1.5	12.00
马丁斯维尔赛车场	0.526	12.00
新罕布什尔国际赛车场	1.058	12.00
加州赛车场	2	14.00
肯塔基赛车场	1.5	14.00
里士满国际赛车场	0.75	14.00
堪萨斯赛车场	1.5	15.00
密歇根国际赛车场	2	18.00
纳什维尔赛车场	0.596	18.00
北卡罗来纳赛车场	1.017	22.00
达灵顿赛车场	1.366	23.00
亚特兰大赛车场	1.54	24.00
多佛唐斯国际赛车场	1	24.00
Lowe's 汽车赛场	1.5	24.00
德克萨斯州汽车赛场	1.5	24.00
代托纳国际赛车场	2.5	31.00
塔拉迪加超级赛车场	2.66	33.00
布里斯托尔赛车场	0.533	36.00

来源: FSN的梦幻赛车区

几何属性

典型的水平曲线（平面视图）

水平曲线出现在两条道路交叉的地方，为两条道路之间提供平缓的过渡。两条道路的交点定义为切点交点（PI）。曲线的起点位置定义为曲线起点（PC），而曲线的终点位置定义为切点（PT）。PC 距离 PI 为 $T$，其中 $T$ 被定义为切线长度。切线长度可以通过找到曲线的中心角（以度为单位）来计算。该角度等于两条道路切线之间的内角的补角。

$T=R\tan \left({\frac {\Delta }{2}}\right)\,\!$

其中

• $T\,\!$= 切线长度（以长度单位为单位）
• $\Delta \,\!$= 曲线的中心角，以度为单位
• $R\,\!$= 曲线半径（以长度单位为单位）

PT 距离 PC 为 $L$，其中 $L$ 被定义为曲线长度。曲线长度可以使用半圆长度公式确定

$L={\frac {R\Delta \pi }{180}}\,\!$

PI 和曲线顶点之间的距离可以很容易地使用 $T$ 和 $R$ 的直角三角形属性来计算。取此距离并减去曲线半径 $R$，可以找到外部距离 $E$，这是曲线和 PI 之间的最小距离。

$E=R\left({{\frac {1}{\cos \left({\frac {\Delta }{2}}\right)}}-1}\right)\,\!$

其中

• $E\,\!$= 外部距离（以长度单位为单位）

类似地，可以找到中垂线$M$。中垂线是连接 PC 和 PT 的直线与曲线的最大距离。它位于曲线顶点和 PI 之间的直线上。

$M=R\left({1-\cos \left({\frac {\Delta }{2}}\right)}\right)\,\!$

其中

• $M\,\!$= 中垂线（长度单位）

类似地，弦长的几何公式可以找到$C$，它代表该曲线的弦长。

$C=2R\sin \left({\frac {\Delta }{2}}\right)\,\!$

视距特性

曲线视距受限

与直线平坦道路拥有很远清晰的视线不同，水平曲线带来了独特的挑战。曲线内侧的自然地形，例如树木、悬崖或建筑物，如果离道路太近，可能会阻挡驾驶员对前方道路的视线。因此，可接受的设计速度通常会降低，以应对视距限制。

计算给定曲线可接受视距时存在两种情况。第一种情况是视距被确定为小于曲线长度。第二种情况是视距超过曲线长度。每种情况都有各自的公式，根据几何特性得出视距。确定哪种情况是正确的，通常需要对两者进行测试，以找出哪一个是真实的。

给定某个视距$S$和已知的曲线长度$L$和内车道中心线半径$R_{v}$，视距障碍物可以离道路内缘的距离$M_{s}$可以根据以下公式计算。

$S<L:M_{s}=R_{v}\left({1-\cos {\frac {28.65S}{R_{v}}}}\right)\,\!$

$S>L:M_{s}=R_{v}\left({1-\cos {\frac {28.65L}{R_{v}}}}\right)+\left({\frac {S-L}{2}}\right)\sin \left({\frac {28.65L}{R_{v}}}\right)\,\!$

演示

• Flash 动画：路边净空区（Karen Dixon 和 Thomas Wall 制作）
• Flash 动画：超高（Karen Dixon 和 Thomas Wall 制作）

示例

示例 1：曲线半径

问题

问题

一条弯曲的公路设计速度为 110 公里/小时。在一条水平曲线处，超高设置为 6.0%，侧向摩擦系数为 0.10。确定提供安全车辆运行的最小曲线半径。

示例

解决方案

$R={\frac {v^{2}}{g\left({e+f_{s}}\right)}}={\frac {{(110*{(1000/3600))}}^{2}}{9.8\left({.06+0.10}\right)}}=595\ meters\,\!$

示例 2：确定里程

问题

问题

一个水平曲线设计为半径 600 米，已知切线长为 52 米。PI 位于里程 200+00。确定 PT 的里程。

示例

解决方案

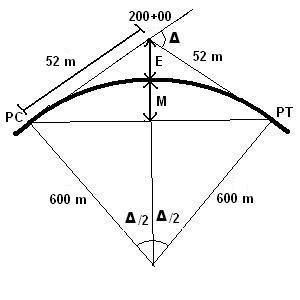本问题已知信息

$T=R\tan \left({\frac {\Delta }{2}}\right)\,\!$

$52=600\tan \left({\frac {\Delta }{2}}\right)\,\!$

${\Delta }=9.9\deg \,\!$

$L={\frac {R\pi \Delta }{180}}={\frac {600\pi 9.9}{180}}=104\,\!$

$PC=PI-T=200+00\ -\ 0+52\ =199+48\,\!$

$PT=PC+L=199+48\ +\ 1+04\ =200+52\,\!$

示例 3：停车视距

问题

问题

一条单向赛道上非常长的水平曲线，其中心线半径为 1750 米，两条车道宽 4 米，设计车速为 200 公里/小时。确定从赛道内侧边缘到观众可以停车的最近距离，而不会阻碍驾驶员所需的视距。假设视距小于曲线的长度，摩擦系数为 0.3，感知反应时间为 2.5 秒。

示例

解决方案

中心线半径为 1750 米，内侧车道中心线距离顶点 1748 米（1750 - (4/2)）。使用停车视距公式（参见 视距），计算得 SSD 为 664 米。由此，可以很容易地找到观众可以停车的位置距离赛道的距离。

$S<L:M_{s}=R_{v}\left({1-\cos {\frac {28.65S}{R_{v}}}}\right)=1748\left({1-\cos {\frac {28.65(664)}{1748}}}\right)=31.43\ meters\,\!$

这得出了到内侧车道中心的距离（31.43 米）。减去一半的车道宽度（在本例中为 2 米）即可得到到赛道边缘的距离，即 29.43 米。

示例问题

问题 (解答)

演示

• 视频：水平线形、水平过渡和超高

其他问题

• 作业
• 其他问题

变量

• $R$ - 中心线曲线半径
• $D_{a}$ - 曲线度 [水平曲线 30.5 米（100 英尺）弧长所对应的角度
• $T$ - 切线长（以长度单位表示）
• $\Delta$ - 曲线切线的偏转角。 也是曲线的中心角，以度为单位。
• $E$ - 外部。 曲线与PI之间的最小距离
• $M$ - 中垂线
• $L$ - 曲线长度
• $C$ - 弦长
• $S$ - 视距
• $M_{s}$ - 可接受的视线障碍物放置在道路内缘的距离，不会阻碍视线距离
• $R_{v}$ - 最内侧车道中心线的半径

关键术语

• PC: 曲线起点
• PI: 切线交点
• PT: 切线终点