小学几何/角

在本节中，我们将讨论角。

角

角（∠）由顶点（一个点）、两条边（射线）和一个弧组成。它们被排列起来，使得边的端点与顶点相同，弧从一边延伸到另一边。角的大小取决于边的张开程度，用度数来衡量。你可以用量角器放在顶点上，看看你的第二条边到达了多少度来测量它们。

小于90°的角称为锐角。90°角称为直角。介于90°和180°之间的角称为钝角。正好是180°的角称为平角。介于180°和360°之间的角称为优角，而360°角称为周角。

角通常以它包含的点来命名。格式如下

"∠" + 一条边上的一个点 + 顶点 + 另一条边上的一个点

但是，有时在该顶点上没有角，我们可以省略边上的点。实际上，当我们懒惰的时候，我们甚至可以用一个小写字母来代表一个特定的角。注意，在这种情况下，必须省略∠。虽然小写字母代表角的值，但所有这些名称都可以在方程中用作未知数。

邻角（adj. ∠s）是指

1. 它们的相对边重合（叠加）；
2. 它们的弧不重合（叠加）；
3. 它们的顶点重合（叠加）。

有时，两个角可能加起来等于90°或180°。它们分别称为余角和补角。由于许多角都具有这样的性质，这些性质在将来会非常有用。

点角

有时，两个或多个角共享一个公共顶点，并且它们的大小加起来等于360^o。它们称为点角（∠s at a pt.）。这在证明或找出角的时候非常有用。

例如，想象一下O是图形中的一个点。三个点A、B和C围绕点O，分别从O射出到A、B和C。已知∠AOB = 120°，∠BOC = 150°，

${\begin{aligned}\angle AOB+\angle BOC+\angle COA&=360^{\circ }(\angle s{\text{ at a pt.}})\\120^{\circ }+150^{\circ }+\angle COA&=360^{\circ }\\\angle COA&=360^{\circ }-120^{\circ }-150^{\circ }\\&=90^{\circ }\end{aligned}}$

直线上的邻角

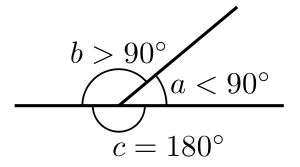
当邻角的大小加起来等于180°时，它们是直线上的邻角。它们用于找出其中一个角的值。（或者更多，当你有相等或相关的角时。）缩写adj. ∠s on st. line可以作为参考，表明这些角加起来等于180°。

以右边的图像为例。这里，b和a是互补的。b和a的和等于c。b和a是直线上的邻角。如果我们知道b的值，我们可以很容易地找出a的值。注意，a、b和c是点角。

对顶角

对顶角非常简单。如果两条直线相交，产生的相对角必须是对顶角（vert. opp. ∠s）。它们必须彼此相等。注意，你不能仅仅通过观察就假设某物是直线，所以在做任何事情之前，请确保它在题目中被提到。对顶角是一个非常常见的参考，在许多情况下会派上用场，所以在你遇到问题之前，先看看是否能找到一些对顶角。

看右边那张图。如图所示，D等于C，A等于B。这是因为它们是对顶角。注意，这里，D和A，A和C，C和B，以及D和B都是直线上的邻角对。此外，这四个角是点角。