小学几何/等边三角形的作图

小学几何
我们的工具：尺子和圆规	作图等边三角形	复制线段

引言

在这一章中，我们将向你展示如何画一个等边三角形。什么是“等边”？它仅仅意味着三角形的三条边长度相同。

任何顶点（点）为A、B和C的三角形写作： $\triangle ABC$ .

如果是等边三角形，它将看起来像图片中的那样。

在欧几里得《几何原本》中，相关内容可以在《几何原本》第一卷命题1的第31页找到，这是伊萨克·托德亨特在1872年的翻译中，为学校和大学使用的欧几里得几何原本。

使用你的尺子，画一条线段，长度任意，只要是你想要的三角形的边长即可。
将线段的一端称为A，另一端称为B。
现在你有一条名为 ${\overline {AB}}$ 的线段。
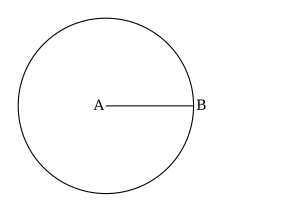
它应该看起来像下面的图画。
使用你的圆规，画圆 $\circ A,$ ，其圆心为A，半径为 ${\overline {AB}}$ 。
再次使用你的圆规画圆 $\circ B,{\overline {AB}}$ ，其圆心为B，半径为 ${\overline {AB}}$ 。
你能看到圆圈是如何相交（互相交叉）于两点的吗？
这些点在下图中用红色显示。
选择其中一个点并将其称为C。
我们选择了上面的点，但如果你喜欢，也可以选择下面的点。如果你选择下面的点，你的三角形会看起来“倒置”，但它仍然是一个等边三角形。
画一条线段，连接A和C，得到线段 ${\overline {AC}}$ 。
画一条线段，连接B和C，得到线段 ${\overline {BC}}$ 。
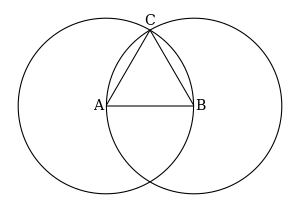
三角形 $\triangle ABC$ 的作图已完成。

三角形 $\triangle ABC$ 是一个等边三角形。

点B和C都在圆 $\circ A,{\overline {AB}}$ 的圆周上，点A在圆心。
因此，线段 ${\overline {AB}}$ 与线段 ${\overline {AC}}$ 的长度相同。它们都是圆 $\circ A$ 的半径，或者更简单地说， ${\overline {AB}}={\overline {AC}}$ 。
对另一个圆我们也做同样的事情。
点 **A** 和 **C** 都在圆 $\circ B,{\overline {AB}}$ 的圆周上，点 **B** 位于圆心。
所以我们可以说 ${\overline {AB}}={\overline {BC}}$ 。
我们已经证明了 ${\overline {AB}}={\overline {AC}}$ 和 ${\overline {AB}}={\overline {BC}}$ 。由于 ${\overline {AC}}$ 和 ${\overline {BC}}$ 的长度都等于 ${\overline {AB}}$ ，它们也必须彼此相等。这可以通过替换来证明。所以我们可以说 ${\overline {AC}}={\overline {BC}}$
因此，线段 ${\overline {AB}}$ ， ${\overline {AC}}$ 和 ${\overline {BC}}$ 都相等。 ${\overline {AB}}={\overline {AC}}={\overline {BC}}$
我们证明了 $\triangle ABC$ 的所有边都相等，所以根据定义，这个三角形是等边三角形。