Haskell/理解箭头

箭头，就像单子一样，表达了在特定上下文中发生的计算。但是，它们比单子更抽象，因此允许使用单子类无法实现的上下文。这两种抽象之间的本质区别可以概括为

正如我们将单子类型 m a 视为“提供 a 的计算”；我们也将箭头类型 a b c（即参数化类型 a 对两个参数 b 和 c 的应用）视为“具有 b 类型输入并提供 c 的计算”；箭头将对输入的依赖关系明确地表示出来。

——John Hughes，将单子泛化为箭头

本章主要分为两部分。首先，我们将考虑箭头计算与我们习惯的函子类所表达的计算的主要区别，并将简要介绍一些与箭头相关的核心类型类。其次，我们将研究 John Hughes 在箭头最初的介绍中使用的解析器示例。

Arrow 速查指南

箭头看起来很像函数

理解箭头的第一步是认识到它们与函数有多相似。与 (->) 一样，Arrow 实例的类型构造函数的种类是 * -> * -> *，也就是说，它接受两个类型参数——不像 Monad，它只接受一个。重要的是，Arrow 以 Category 作为超类。Category 大致来说是表示可以像函数一样组合的事物的类

class Category y where
    id  :: y a a                   -- identity for composition.
    (.) :: y b c -> y a b -> y a c -- associative composition.

函数具有 Category 的实例——事实上，它们也是 Arrow。

这种相似性的一个实际结果是，在查看充满 Arrow 运算符的表达式时，您必须以无点方式思考，例如 教程 中的这个示例

(total &&& (const 1 ^>> total)) >>> arr (uncurry (/))

否则，您将很快迷失在寻找应用事物的值的过程中。无论如何，即使以正确的方式查看此类表达式，也很容易迷失方向。这就是 proc 符号的意义所在：在使某些运算符隐式的情况下添加额外的变量名称和空格，以便 Arrow 代码更容易理解。

在继续之前，我们应该提到 Control.Category 还定义了 (<<<) = (.) 和 (>>>) = flip (.)，这非常常用，用于从左到右组合箭头。

Arrow 在 Applicative 和 Monad 之间滑动

尽管我们上面给出了警告，但箭头可以与 applicative 函子 和 单子 相比。诀窍是使函子看起来更像箭头，而不是相反。也就是说，您不应该将 Arrow y => y a b 与 Applicative f => f a 或 Monad m => m a 进行比较，而应该与

• Applicative f => f (a -> b)，静态态射的类型，即 (<*>) 左侧的值；以及
• Monad m => a -> m b，Kleisli态射的类型，即 (>>=) 右侧的函数 。

态射是可以具有 Category 实例的，事实上我们可以为静态态射和 Kleisli态射都编写 Category 的实例。这种小小的扭转足以进行合理的比较。

如果这个论证让您想起了关于 能力滑梯 的讨论，其中我们比较了 Functor、Applicative 和 Monad，那么这是一个表明您注意到了的迹象，因为我们正在遵循完全相同的路线。在那次讨论中，我们提到态射的类型限制了它们可以或不能创建的效果。单子绑定可以根据提供给 Kleisli态射的 a 值，对计算的效果进行近乎任意的更改，而 applicative 计算中函子包装器和函数箭头之间的隔离意味着 applicative 计算中的效果根本不依赖于函子中的值 。

从这个角度来看，箭头与之不同之处在于，在Arrow y => y a b中，上下文y与函数箭头之间不存在这种联系来严格确定可能性的范围。静态和 Kleisli 态射都可以被制成Arrow，反之，Arrow的实例也可以被制成像Applicative一样有限，或者像Monad一样强大。更有趣的是，我们可以使用Arrow来采取第三种选择，在一个上下文中同时拥有类似于应用函子的静态效果和类似于单子的动态效果，但它们彼此分离。箭头使我们能够微调如何组合效果。这是基于箭头的解析器经典示例的主要推动力，我们将在本章末尾对其进行研究。

Arrow可以多任务处理

这些是Arrow的方法

class Category y => Arrow y where
    -- Minimal implementation: arr and first
    arr    :: (a -> b) -> y a b                 -- converts function to arrow
    first  :: y a b -> y (a, c) (b, c)          -- maps over first component

    second :: y a b -> y (c, a) (c, b)          -- maps over second component
    (***)  :: y a c -> y b d -> y (a, b) (c, d) -- first and second combined
    (&&&)  :: y a b -> y a c -> y a (b, c)      -- (***) on a duplicated value

通过这些方法，我们可以对看起来像是线性箭头链的每一步进行多个计算。这是通过将用于独立计算的值作为（可能是嵌套的）对中的元素来保留，然后使用对处理函数在需要时访问每个值来完成的。例如，这允许保存中间值供以后使用，或者方便地使用具有多个参数的函数。

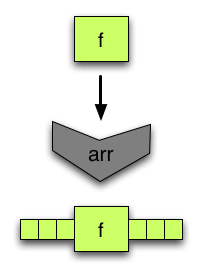
可视化可能有助于理解箭头计算中的数据流。以下是(>>>)和五个Arrow方法的说明

• 
  arr将函数转换为箭头，可以与其他箭头组合。当然，并非所有箭头都是以这种方式创建的。
• 
  (>>>)组合两个箭头。第一个箭头的输出被馈送到第二个箭头。
• 
  first并排接受两个输入。第一个使用箭头进行修改，而第二个保持不变。
• 
  相反，second接受两个输入，但只修改第二个。
• 
  (***)接受两个输入，并使用两个箭头对它们进行修改，每个输入一个箭头。
• 
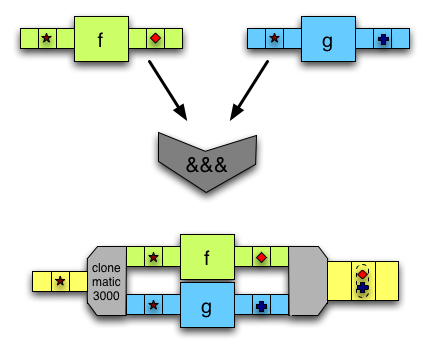
  (&&&)接受一个输入，将其复制，并使用不同的箭头修改每个副本。

来自教程的mean1箭头的数据流。矩形是箭头，圆角矩形是使用arr创建的箭头，圆圈是其他数据流拆分/合并点。其他组合器被隐含。对应代码

(total &&& (const 1 ^>> total))
    >>> arr (uncurry (/))

值得一提的是，Control.Arrow 将returnA = arr id 定义为一个不执行任何操作的箭头。箭头定律之一指出returnA必须等效于Category实例中的id。

ArrowChoice可以是坚决的

如果Arrow使多任务处理成为可能，那么ArrowChoice会强制执行对要执行的任务的决策。

class Arrow y => ArrowChoice y where
    -- Minimal implementation: left
    left  :: y a b -> y (Either a c) (Either b c)          -- maps over left choice

    right :: y a b -> y (Either c a) (Either c b)          -- maps over right choice
    (+++) :: y a c -> y b d -> y (Either a b) (Either c d) -- left and right combined
    (|||) :: y a c -> y b c -> y (Either a b) c            -- (+++), then merge results

Either提供了一种对值进行标记的方法，以便不同的箭头可以根据它们是否用Left或Right进行标记来处理它们。请注意，这些涉及Either的方法与Arrow提供的涉及对的方法完全类似。

来自教程的getWord示例片段中的数据流。蓝色表示Left标记，红色表示Right标记。请注意，proc表示法的if结构将True发送到Left，将False发送到Right。对应代码

proc () -> do
  firstTime <- oneShot -< ()
  mPicked <- if firstTime
    then do
      picked <- pickWord rng -< ()
      returnA -< Just picked
    else returnA -< Nothing
  accum' Nothing mplus -< mPicked

ArrowApply只是无聊的

顾名思义，ArrowApply使我们能够在箭头计算过程中直接将箭头应用于值。普通的Arrow不允许这样做——我们只能不停地组合它们。应用只发生在最后，一旦使用某种运行箭头函数从箭头中获得一个普通函数。

class Arrow y => ArrowApply y where
    app :: y (y a b, a) b -- applies first component to second

（例如，函数的app是uncurry ($) = \(f, x) -> f x。）

然而，app需要付出高昂的代价。将箭头作为箭头计算中的值构建，然后通过应用消除它，这意味着允许计算中的值影响上下文。这听起来很像单子绑定所做的事情。事实证明，只要遵循ArrowApply定律，ArrowApply就完全等效于某些Monad。最终的结果是，ArrowApply箭头无法实现Arrow允许但Monad不允许的任何有趣可能性，例如具有部分静态上下文。

箭头真正的灵活之处在于那些不是单子的箭头，否则它就只是一个更笨拙的语法。

——菲利帕·考德罗伊

箭头组合器出现在意想不到的地方

函数是箭头的琐碎示例，因此上面显示的所有Control.Arrow函数都可以与它们一起使用。因此，在与箭头无关的代码中看到箭头组合器是很常见的。以下是它们对普通函数的作用的总结，以及其他模块中可以以相同方式使用的组合器（如果您更喜欢备选名称，或者只是更喜欢对简单任务使用简单模块）。

组合器	它做什么 （专门用于(->)）	备选方案
(>>>)	flip (.)
first	\f (x, y) -> (f x, y)	first (Data.Bifunctor)
second	\f (x, y) -> (x, f y)	fmap; second (Data.Bifunctor)
(***)	\f g (x, y) -> (f x, g y)	bimap (Data.Bifunctor)
(&&&)	\f g x -> (f x, g x)	liftA2 (,) (Control.Applicative)
left	映射到Left情况。	first (Data.Bifunctor)
right	映射到Right情况。	fmap; second (Data.Bifunctor)
(+++)	映射到两种情况。	bimap (Data.Bifunctor)
(|||)	消除Either。	either (Data.Either)
app	\(f, x) -> f x	uncurry ($)

Data.Bifunctor模块提供了Bifunctor类，对和Either是它的实例。Bifunctor非常类似于Functor，只是有两个独立的方法可以将函数映射到它，分别对应于first和second方法。

练习
编写second、(***)和(&&&)的实现。只使用(>>>)、arr和first（加上任何普通函数）来实现second；之后，一旦您实现了它们，就可以使用其他组合器。 编写right的实现，用left表示。 实现liftY2 :: Arrow y => ‌(a -> b -> c) -> y r a -> y r b -> y r c

使用箭头

避免泄漏

箭头最初是由 Swierstra 和 Duponcheel发现的一种高效解析器设计所驱动。为了有一个参考点来讨论其设计的好处，让我们快速看一下单子解析器是如何工作的。

这是一个非常简陋的单子解析器类型的说明

newtype Parser s a = Parser { runParser :: [s] -> Maybe (a, [s]) }

Parser是一个函数，它接受一个输入流（此处为[s]类型的列表），并且根据它在输入中找到的内容，返回一个结果（[a]类型）和一个流（通常是输入流减去解析器消耗的一些输入），或者Nothing。当我们说解析器成功或失败时，我们指的是它是否产生了结果。虽然现实世界中的解析器类型，如来自 Parsec 的ParsecT，为了提供各种其他功能（尤其是失败时的信息性错误消息）可以复杂得多，但这个简单的Parser对于我们目前的用途已经足够了。

例如，这是一个字符串中单个字符的解析器

char :: Char -> Parser Char Char
char c = Parser $ \input -> case input of
    [] -> Nothing
    x : xs -> if x == c then Just (c, xs) else Nothing

如果输入字符串中的第一个字符是c，则char c成功，消耗第一个字符并给出c作为结果；否则，它失败

GHCi> runParser (char 'H') "Hello"
Just ('H',"ello")
GHCi> runParser (char 'G') "Hello"
Nothing

再次看一下Parser类型，它本质上是Maybe上的State [s]。因此，我们能够将其制成Applicative、Monad、Alternative等等的实例并不奇怪（您可能想尝试一下）。这给了我们一套非常灵活的组合器，用于从更简单的解析器构建更复杂的解析器。解析器可以按顺序运行...

isHel :: Parser Char ()
isHel = char 'H' *> char 'e' *> char 'l' *> pure ()

... 将它们的结果组合起来...

string :: String -> Parser Char String
string = traverse char

... 或者作为彼此的备选方案进行尝试

solfege :: Parser Char String
solfege = string "Do" <|> string "Re" <|> string "Mi"

通过最后一个例子，我们可以指出 Swierstra 和 Duponcheel 试图解决的问题。当 solfege 在字符串 "Fa" 上运行时，我们无法检测到解析器会失败，直到所有三个备选方案都失败。如果我们有更复杂的解析器，其中一个备选方案可能只有在尝试使用大量输入流后才会失败，那么我们就必须以同样的方式沿着解析器链向下遍历。所有可能被后面的解析器使用的输入都必须保留在内存中，以防其中一个解析器能够使用它。这会导致比你想象的更多空间使用——这种情况通常被称为“空间泄漏”。

可以做得更好吗？

Swierstra 和 Duponcheel（1996）注意到，在处理某些类型的解析任务时，一个更智能的解析器可以立即在看到第一个字符时失败。例如，在上面的 solfege 解析器中，第一个字母解析器的选择仅限于字母 'D'、'R' 和 'M'，分别代表 "Do"、"Re" 和 "Mi"。这个更智能的解析器还能够更快地进行垃圾回收，因为它可以向前查看其他解析器是否能够使用该输入，并丢弃无法使用的输入。这个新的解析器很像单子解析器，主要区别在于它导出了“静态”信息。它就像一个单子，但它也会告诉你它可以解析什么。

有一个主要问题。这与 Monad 接口不符。单子组合适用于 (a -> m b) 函数，以及函数本身。没有办法附加静态信息。你只有一个选择，输入一些内容，然后看看它是否通过或失败。

当时这个问题刚出现时，单子接口被宣称为函数式编程社区中一个完全通用的工具，因此发现有一些特别有用的代码无法适应该接口，这是一个挫折。这就是箭头出现的地方。John Hughes 的“将单子泛化为箭头”提出了箭头抽象作为一种新的、更灵活的工具。

静态和动态解析器

让我们从 Hughes 提出的箭头的角度，更详细地检查一下 Swierstra 和 Duponcheel 的解析器。解析器有两个部分：一个快速的静态解析器，它告诉我们输入是否值得尝试解析；以及一个缓慢的动态解析器，它完成实际的解析工作。

import Control.Arrow
import qualified Control.Category as Cat
import Data.List (union)

data Parser s a b = P (StaticParser s) (DynamicParser s a b)
data StaticParser s = SP Bool [s]
newtype DynamicParser s a b = DP ((a, [s]) -> (b, [s]))

静态解析器由一个标志组成，该标志告诉我们解析器是否可以接受空输入，以及可能的“起始字符”列表。例如，单个字符的静态解析器如下所示

spCharA :: Char -> StaticParser Char
spCharA c = SP False [c]

它不接受空字符串（False），可能的起始字符列表仅包含 c。

动态解析器需要更多剖析。我们看到的是一个从 (a, [s]) 到 (b, [s]) 的函数。从两个解析器的顺序的角度思考是有用的：每个解析器都使用前一个解析器的结果（a）以及输入流的剩余部分（[s]），对 a 做一些操作以生成自己的结果 b，使用一些字符串并返回“它”。因此，作为一个实际操作的例子，考虑一个动态解析器 (Int, String) -> (Int, String)，其中 Int 表示到目前为止解析的字符数。下表显示了如果我们将几个解析器组合在一起并在字符串“cake”上运行它们会发生什么。

	结果	剩余部分
之前	0	cake
第一个解析器之后	1	ake
第二个解析器之后	2	ke
第三个解析器之后	3	e

因此，这里要说明的是，动态解析器有两个任务：对前一个解析器的输出做一些操作（非正式地，a -> b），以及使用一部分输入字符串（非正式地，[s] -> [s]），因此类型为 DP ((a,[s]) -> (b,[s]))。现在，对于单个字符的动态解析器（类型为 (Char, String) -> (Char, String)），第一个任务是微不足道的。我们忽略前一个解析器的输出，返回我们解析的字符，并从流中使用一个字符

dpCharA :: Char -> DynamicParser Char a Char
dpCharA c = DP (\(_,_:xs) -> (c,xs))

这可能会让你提出一些问题。例如，如果我们只是要忽略前一个解析器的输出，那么接受它有什么意义呢？而且动态解析器不应该是通过测试 x == c 来确保当前流中的字符与要解析的字符匹配吗？第二个问题的答案是否定的——事实上，这是重点的一部分：这项工作并不必要，因为检查已经由静态解析器执行。当然，事情之所以如此简单，是因为我们只测试了一个字符。如果我们要编写一个解析多个字符的解析器，我们就需要实际测试第二个及后续字符的动态解析器；如果我们要通过链接多个字符解析器来构建一个输出字符串，那么我们就需要前一个解析器的输出。

现在将两个解析器组合在一起。这是我们针对单个字符的 S+D 风格的解析器

charA :: Char -> Parser Char a Char
charA c = P (SP False [c]) (DP (\(_,_:xs) -> (c,xs)))

为了实际使用解析器，我们需要一个 runParser 函数，该函数运行静态测试并将动态解析器应用于输入

-- The Eq constraint on s is needed so that we can use elem.
runParser :: Eq s => Parser s a b -> a -> [s] -> Maybe (b, [s])
runParser (P (SP emp _) (DP p)) a []
    | emp = Just (p (a, []))
    | otherwise = Nothing
runParser (P (SP _ start) (DP p)) a input@(x:_)
    | x `elem` start = Just (p (a, input))
    | otherwise = Nothing

请注意，runParser 如何输出一个类型为 [s] -> Maybe (b, [s]) 函数的函数，这本质上与我们之前演示的单子解析器相同。现在我们可以像之前使用 char 一样使用 charA。（主要区别在于作为哑参数传递的 ()。这在这里是有意义的，因为 charA 实际上不使用类型为 a 的初始值。但是，对于其他解析器，情况可能并非如此。）

GHCi> runParser (charA 'D') () "Do"
Just ('D',"o")
GHCi> runParser (charA 'D') () "Re"
Nothing

引入箭头组合器

完成初步的介绍之后，我们现在将为 Parser s 实现 Arrow 类，并通过这样做，让你了解箭头为何有用。所以让我们开始吧

instance Eq s => Arrow (Parser s) where

arr 应该将任意函数转换为解析箭头。在这种情况下，我们必须以非常宽松的意义来使用“解析”：生成的箭头接受空字符串，并且只接受空字符串（它的第一个字符集为 []）。它的唯一作用是获取前一个解析箭头的输出并对其进行操作。因此，它不会使用任何输入。

    arr f = P (SP True []) (DP (\(b,s) -> (f b,s)))

同样，first 组合器也比较简单。给定一个解析器，我们想要生成一个新的解析器，它接受一对输入 (b,d)。输入的第一个部分 b 是我们实际要解析的内容。第二部分保持原样传递

    first (P sp (DP p)) = P sp (DP (\((b,d),s) ->
        let (c, s') = p (b,s)
        in  ((c,d),s')))

我们还需要提供 Category 实例。id 非常明显，因为 id = arr id 必须成立

instance Eq s => Cat.Category (Parser s) where
    id = P (SP True []) (DP (\(b,s) -> (b,s)))
    -- Or simply: id = P (SP True []) (DP id)

另一方面，(.) 的实现需要更多思考。我们想要获取两个解析器，并返回一个组合的解析器，其中包含两个参数的静态解析器和动态解析器

    -- The Eq s constraint is needed for using union here.
    (P (SP empty1 start1) (DP p1)) .
      (P (SP empty2 start2) (DP p2)) =
        P (SP (empty1 && empty2)
              (if not empty1 then start1 else start1 `union` start2))
          (DP (p2.p1))

组合动态解析器很简单；我们只需进行函数组合即可。将静态解析器组合在一起需要一些思考。首先，组合的解析器只有在“两个”解析器都接受空字符串的情况下才能接受空字符串。很公平，现在如何处理起始符号？好吧，解析器应该是按顺序排列的，所以第二个解析器的起始符号实际上并不重要。如果一切都很简单，组合解析器的起始符号将只是 start1。唉，现实并非如此简单，因为解析器很可能会接受空输入。如果第一个解析器接受空输入，那么我们就必须通过接受第一个和第二个解析器的起始符号来考虑这种情况

那么，箭头带给我们什么呢？

如果你回顾我们的 Parser 类型并清空静态解析器部分，你可能会注意到这很像函数的箭头实例。

arr f = \(b, s) -> (f b, s)
first p = \((b, d), s) ->
            let (c, s') = p (b, s)
            in  ((c, d), s'))

id = id
p2 . p1 = p2 . p1

有一个奇怪的 s 变量在其中，这使得定义看起来有些奇怪，但例如 简单的 first 函数 的轮廓就在那里。实际上，你在这里看到的是 State 单子/Kleisli 态射的箭头实例（让 f :: b -> c、p :: b -> State s c 以及 (.) 实际上是 (<=<) = flip (>=>)）。

这很好，但我们可以很容易地在经典的单子风格中使用 bind 来做到这一点，将 first 变为一个奇特的辅助函数，可以用一些模式匹配轻松地编写。但请记住，我们的 Parser 类型不仅仅是动态解析器——它还包含静态解析器。

arr f = SP True []
first sp = sp
(SP empty1 start1) >>> (SP empty2 start2) = (SP (empty1 && empty2)
        (if not empty1 then start1 else start1 `union` start2))

这根本不是一个函数，它只是在操作一些数据类型，而且无法用单子形式表达。但 Arrow 接口也能很好地处理它。当我们将两种类型结合在一起时，我们得到了两全其美的结果：静态解析器数据结构与动态解析器一起使用。Arrow 接口使我们能够以透明的方式将两个解析器（静态和动态）组合在一起并作为单元进行操作，然后我们可以将其作为一个传统的统一函数运行。

Arrows 在实践中的应用

一些使用箭头库的例子

• Opaleye (库文档)，一个用于 SQL 生成的库。
• Haskell XML 工具箱 (项目页面 和 库文档) 使用箭头处理 XML。Haskell Wiki 上有一个页面，其中包含一个较为友好的 HXT 简介。
• Netwire (库文档) 是一个用于 函数式反应式编程 (FRP) 的库。FRP 是一个用于处理事件和随时间变化的值的函数式范式，其用例包括用户界面、模拟和游戏。Netwire 既有箭头接口，也有 applicative 接口。
• Yampa (Haskell Wiki 页面 库文档) 是另一个基于箭头的 FRP 库，是 Netwire 的前身。
• Hughes 的箭头风格解析器最初是在他的 2000 年论文中描述的，但直到 2005 年 5 月 Einar Karttunen 发布了 PArrows，才有了可用的实现。

参见

• 关于箭头的参考书目（haskell.org）

鸣谢

本模块使用来自 Shae Erisson 编写的 箭头入门 中的文本，最初为 The Monad.Reader 4 编写。