Haskell/Zippers

忒修斯与拉链

迷宫

"忒修斯，我们必须做点什么"，古希腊公司首席营销官荷马说。忒修斯将米诺陶洛斯™动作模型放回架子上，点了点头。"现在的孩子们不再对古老的神话感兴趣，他们更喜欢现代英雄，比如蜘蛛侠或海绵宝宝。"英雄。忒修斯很清楚，当年在克里特岛的迷宫里，他是多么的英雄。但那些"现代英雄"甚至没有试图表现得真实。是什么让他们如此成功？无论如何，如果即将到来的销售问题无法解决，股东肯定会为古希腊公司安排一条通往冥河的通道。

"尤里卡！忒修斯，我有一个主意：我们把你的故事与米诺陶洛斯的故事做成电脑游戏！你认为怎么样？" 荷马是对的。已经出版了几本书，史诗般的（而且打破排行榜的）歌曲，一部必看的电影三部曲，以及无数的忒修斯与米诺陶洛斯™小玩意，但就是没有电脑游戏。"完美，那就这样吧。现在，忒修斯，你的任务是实现这个游戏"。

作为一个真正的英雄，忒修斯选择 Haskell 作为语言来实现公司东山再起的产品。当然，探索米诺陶洛斯的迷宫将成为游戏的一大亮点。他沉思道："我们有一个二维迷宫，它的走廊可以指向多个方向。当然，我们可以从详细的长度和角度抽象出来：为了找到出路，我们只需要知道路径是如何分叉的。为了简化，我们将迷宫建模为一棵树。这样，在深入行走时，分叉的两支就无法再次连接，玩家也无法走回原路。但我认为迷路的机会已经足够了；这样，如果玩家足够耐心，他们就可以用左手法则探索整个迷宫。"

data Node a = DeadEnd a
            | Passage a (Node a)
            | Fork    a (Node a) (Node a)

一个示例迷宫及其树状表示。

忒修斯让迷宫的节点携带一个额外的类型为 a 的参数。稍后，它可能会包含游戏相关信息，比如节点所指地点的坐标、周围的环境、地板上的游戏物品列表或在该迷宫区域游荡的怪物列表。我们假设有两个辅助函数

get :: Node a -> a
put :: a -> Node a -> Node a

检索和更改存储在 Node a 每个构造函数的第一个参数中的类型为 a 的值。

练习
实现 get 和 put。get 的一个情况是 get (Passage x _) = x. 为了得到一个具体的例子，将图片中显示的迷宫写成类型为 Node (Int,Int) 的值。额外的参数 (Int,Int) 持有一个节点的笛卡尔坐标。

"嗯，如何表示玩家在迷宫中的当前位置？玩家可以通过选择左右分支来探索更深的地方，就像在"

 turnRight :: Node a -> Maybe (Node a)
 turnRight (Fork _ l r) = Just r
 turnRight _            = Nothing

"但用这种方式将当前迷宫的顶部替换为相应的子迷宫是不可能的，因为这样玩家就无法返回。"他沉思道。"啊，我们可以应用阿里阿德涅的线绳技巧来返回。我们只需要用玩家线绳经过的分支列表来表示玩家的位置，迷宫始终保持不变。"

data Branch = KeepStraightOn
            | TurnLeft
            | TurnRight
type Thread = [Branch]

用阿里阿德涅的线绳表示玩家的位置。

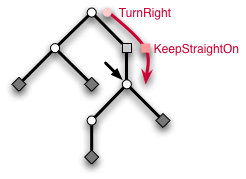
"例如，一条线绳 [TurnRight,KeepStraightOn] 表示玩家在入口处选择了右边的分支，然后直走了一条 Passage 来到达他们当前的位置。有了线绳，玩家现在可以通过延长或缩短线绳来探索迷宫。例如，函数 turnRight 通过将 TurnRight 附加到线绳上来延长线绳。"

turnRight :: Thread -> Thread
turnRight t = t ++ [TurnRight]

"要访问额外的数据，即游戏相关物品等等，我们只需要沿着线绳进入迷宫即可。"

retrieve :: Thread -> Node a -> a
retrieve []                  n             = get n
retrieve (KeepStraightOn:bs) (Passage _ n) = retrieve bs n
retrieve (TurnLeft      :bs) (Fork _ l r)  = retrieve bs l
retrieve (TurnRight     :bs) (Fork _ l r)  = retrieve bs r

练习
编写一个函数 update，它将类型为 a -> a 的函数应用于玩家位置的额外数据。

忒修斯对这种解决方案的满意并没有持续很久。"不幸的是，如果我们要延长路径或后退一步，我们必须更改列表的最后一个元素。我们可以将列表存储为反向，但即使这样，我们也必须反复沿着线绳走来访问玩家位置的迷宫中的数据。这两个操作都需要与线绳长度成正比的时间，对于大型迷宫来说，这将花费太长时间。有没有其他办法？"

阿里阿德涅的拉链

虽然忒修斯是一位技艺高超的战士，但他并没有在编程方面进行太多训练，也无法找到一个令人满意的解决方案。经过了激烈的但无果的思考后，他决定打电话给他的前爱人阿里阿德涅，向她寻求建议。毕竟，是她想出了线绳的主意。
"阿里阿德涅咨询。我能为您做什么？"
我们的英雄立刻认出了这个声音。
"你好阿里阿德涅，我是忒修斯。"
一阵令人不安的沉默暂停了对话。忒修斯清楚地记得，他曾在纳克索斯岛上抛弃了她，他知道她不会喜欢他的电话。但古希腊公司正走在通往冥府的道路上，他没有选择。
"嗯，亲爱的，... 你好吗？"
阿里阿德涅冷冷地反驳道：" 忒修斯先生，亲爱的的日子早就过去了。你想干什么？"
"嗯，我，呃……我需要一些关于编程问题的帮助。我正在编程一个新的忒修斯与米诺陶洛斯™电脑游戏。"
她嘲讽道，"又是为了美化你‘英勇存在’的另一件文物？你还想让我帮你？"
"阿里阿德涅，求求你了，古代极客公司正濒临破产。这款游戏是我们最后的希望！"
停顿了一会儿，她做出了决定。
"好吧，我会帮你。但你必须把古代极客公司的大部分股份转让给我。比如百分之三十。 "
忒修斯脸色苍白。但他又能怎么办呢？情况已经糟糕到无法挽回的地步，于是他同意了，但只在将阿里阿德涅的股份比例降至十分之一后才同意。

忒修斯告诉阿里阿德涅他心目中的迷宫表示后，她立即给出建议，
"你需要一个拉链。 "
"什么？这问题和我的拉链有什么关系？"
"没什么，它是一个由热拉尔·惠特首次发布的数据结构。 "
"哦。"
"更准确地说，它是一种纯粹的函数式方法，用于用一个焦点或指针增强树形数据结构（如列表或二叉树），该指针指向数据结构内部的子树，并允许在它所指的位置进行恒定时间更新和查找。在我们的案例中，我们希望玩家的位置处于焦点。 "
"我知道我自己想要快速更新，但我该怎么编写代码呢？"
"不要着急，你不能通过编码解决问题，你只能通过思考来解决问题。在纯粹的函数式数据结构中，我们能获得恒定时间更新的唯一位置是顶层节点。因此，焦点必须始终在顶部。目前，你迷宫中的顶层节点始终是入口，但你之前将迷宫替换为其子迷宫的想法确保了玩家的位置始终在顶层节点。 "
"但问题是，如何返回，因为所有那些玩家没有选择分支进入的子迷宫都丢失了。"
"你可以使用我的线，这样就不会丢失子迷宫。 "
阿里阿德涅享受着忒修斯的困惑，但在他抱怨已经用过她的线之前，她迅速继续说道，
"关键是将丢失的子迷宫粘贴到线上，这样它们实际上就不会丢失。目的是让线和当前的子迷宫互相补充形成整个迷宫。‘当前’子迷宫是指玩家所处位置的迷宫。拉链仅仅由线和当前的子迷宫组成。 "

type Zipper a = (Thread a, Node a)

拉链是阿里阿德涅的线和玩家所处位置的当前子迷宫的配对。主线是红色的，并有子迷宫连接到它，因此整个迷宫可以从配对中重建。

忒修斯什么也没说。
"你也可以将线视为上下文，当前的子迷宫就位于该上下文中。现在，让我们找出如何定义Thread a。顺便说一下，Thread必须接受额外的参数a，因为它现在存储了子迷宫。线仍然是一个简单的分支列表，但分支与以前不同。 "

data Branch a  = KeepStraightOn a
               | TurnLeft  a (Node a)
               | TurnRight a (Node a)
type Thread a  = [Branch a]

"最重要的是，TurnLeft和TurnRight都有一个子迷宫粘贴到它们上面。当玩家选择比如向右转时，我们用一个TurnRight扩展线，并将未选择的左分支附加到它上面，这样就不会丢失它。 "
忒修斯打断道："等等，我该如何将此行为实现为一个函数turnRight？TurnRight的第一个参数a类型是什么？啊，我明白了。我们不仅需要粘贴会丢失的分支，还需要粘贴Fork的额外数据，因为否则也会丢失。所以，我们可以通过一个初步的"来生成一个新的分支

branchRight (Fork x l r) = TurnRight x l

"现在，我们必须以某种方式用它来扩展现有的线。"
"确实。关于线的第二个要点是，它是反向存储的。要扩展它，你需要在列表前面添加一个新的分支。要返回，你需要删除最顶层的元素。 "
"啊哈，这使得扩展和返回只需要花费恒定时间，而不是像我之前的版本那样花费与长度成正比的时间。所以turnRight的最终版本是"

turnRight :: Zipper a -> Maybe (Zipper a)
turnRight (t, Fork x l r) = Just (TurnRight x l : t, r)
turnRight _               = Nothing

从入口处获取右子树。当然，线最初是空的。请注意，线是反向运行的，即最顶层的段是最新的段。

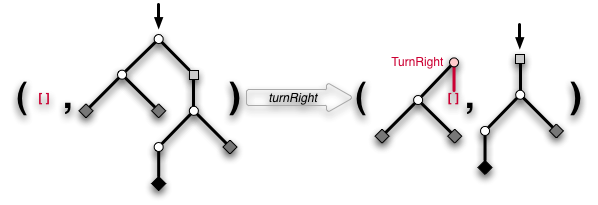
"这并不难。那么，让我们继续keepStraightOn，用于向下走过通道。这比选择分支更容易，因为我们只需要保留额外的数据："

keepStraightOn :: Zipper a -> Maybe (Zipper a)
keepStraightOn (t, Passage x n) = Just (KeepStraightOn x : t, n)
keepStraightOn _                = Nothing

现在向下走过通道。

练习
编写函数turnLeft。

他高兴地说："但有趣的部分是返回，当然。让我们看看……"

back :: Zipper a -> Maybe (Zipper a)
back ([]                   , _) = Nothing
back (KeepStraightOn x : t , n) = Just (t, Passage x n)
back (TurnLeft  x r    : t , l) = Just (t, Fork x l r)
back (TurnRight x l    : t , r) = Just (t, Fork x l r)

"如果线是空的，我们就已在迷宫的入口处，无法返回。在所有其他情况下，我们必须绕线。由于附加到线上的元素，我们实际上可以重建我们来自的子迷宫。"
阿里阿德涅评论道，"请注意，一个部分正确性测试是检查每个绑定变量（如x、l和r）在等号左侧是否只出现一次，在等号右侧也只出现一次。所以，当上下移动拉链时，我们只是在线和当前子迷宫之间重新分配数据。 "

练习
现在我们可以导航拉链了，编写函数get、put和update，这些函数对玩家位置的额外数据进行操作。 拉链绝不局限于具体的例子Node a，它们可以为所有树形数据类型构建。继续构建一个用于二叉树的拉链 data Tree a = Leaf a | Bin (Tree a) (Tree a) 首先考虑线可以采取的可能分支Branch a。探索树时，你需要将什么粘贴到线上？ 简单的列表也有拉链。 data List a = Empty | Cons a (List a) 它看起来像什么？ 编写一个基于忒修斯迷宫的完整游戏。

尤里卡！这就是忒修斯想要的解决方案，古代极客公司应该会成功，即使部分出售给了阿里阿德涅咨询公司。但还有一个问题
"为什么它被称为拉链？"
"嗯，我会称它为‘阿里阿德涅的珍珠项链’。但最有可能的是，它被称为拉链，是因为线类似于拉链的开口部分，而子迷宫类似于拉链的闭合部分。在数据结构中移动类似于拉开或合上拉链。 "
"‘阿里阿德涅的珍珠项链’，”他轻蔑地说。“就好像你的线在克里特岛上帮过什么忙一样。”
"就好像线的想法是你的，”她回答道。 "
"呸，我不需要线，”他否认了实际上确实需要线来编程游戏的事实。
令他惊讶的是，她同意了，"嗯，你确实不需要线。另一个观点是，用你的手指抓住树的焦点，将其举到空中。焦点将位于顶部，树的所有其他分支都垂下来。你只需要将得到的树分配一个合适代数数据类型，最可能的是拉链的类型。 "

用你的手指抓住焦点，将其举到空中，垂下的分支将形成一个新的树，你的手指位于顶部，准备通过一个代数数据类型进行结构化。

"哦。”他不需要阿里阿德涅的线，但他需要阿里阿德涅告诉他？这太过了。
"谢谢你，阿里阿德涅，再见。"
他看不见她，所以她并没有掩饰她狡黠的微笑。

练习
取一个列表，用你的手指固定中间的一个元素，然后将列表举到空中。你可以给得到的树赋予什么类型？

半年后，忒修斯停在一家商店的橱窗前，无视试图从他扣紧的夹克下钻进来的冰冷雨水。闪烁的字母宣告道

"蜘蛛侠：迷失在网络中"

- 在线的迷宫中找到你的出路 -
古代极客公司出品的伟大电脑游戏

他诅咒自己打电话给阿里阿德涅并将公司的一部分卖给了她那天。是她在策划由阿里阿德涅的丈夫狄俄尼索斯领导的WineOS公司的不友好收购吗？忒修斯看着雨滴沿着玻璃窗流下来。在生产线改变之后，再也没有人会生产忒修斯与米诺陶洛斯™商品了。他叹了口气。他的时代，英雄的时代，结束了。现在是超级英雄的时代了。

数据类型的区分

上一节介绍了拉链，一种用指针增强树形数据结构Node a的方法，该指针可以聚焦于不同的子树。虽然我们为特定的数据结构Node a构建了一个拉链，但可以通过手动方式轻松地将构建方法调整到不同的树形数据结构。

练习
从三叉树开始 data Tree a = Leaf a | Node (Tree a) (Tree a) (Tree a) 并推导出相应的Thread a和Zipper a。

机械微分

但也有一个完全机械的方式来推导出任何（适当规则的）数据类型的拉链。令人惊讶的是，“推导”必须从字面上理解，因为拉链可以通过数据类型的导数获得，这是科诺尔·麦克布莱德首次描述的发现。下一节将阐述这颗真正奇妙的数学宝石。

为了进行系统性构建，我们需要用类型进行计算。类型结构化计算的基础知识在单独的章节泛型编程中概述，我们将严重依赖这些材料。

让我们看一些例子，看看它们的拉链有什么共同点以及它们如何暗示差异。二叉树的类型是递归方程的固定点

${\mathit {Tree2}}=1+{\mathit {Tree2}}\times {\mathit {Tree2}}$.

当沿着树向下走时，我们迭代地选择进入左子树或右子树，然后将未进入的子树粘贴到阿里阿德涅的线。因此，我们线的分支类型为

${\mathit {Branch2}}={\mathit {Tree2}}+{\mathit {Tree2}}\cong 2\times {\mathit {Tree2}}$.

类似地，三叉树的线

${\mathit {Tree3}}=1+{\mathit {Tree3}}\times {\mathit {Tree3}}\times {\mathit {Tree3}}$

具有类型为

${\mathit {Branch3}}=3\times {\mathit {Tree3}}\times {\mathit {Tree3}}$

因为在每一步，我们可以在三个子树之间选择，并且必须存储我们没有进入的两个子树。这与导数${\frac {d}{dx}}x^{2}=2\times x$ 和 ${\frac {d}{dx}}x^{3}=3\times x^{2}$ 有惊人的相似之处吗？

解开这个谜团的关键是数据结构的单孔上下文的概念。想象一个数据结构，它以类型 $X$ 为参数，就像树的类型 ${\mathit {Tree}}\,X$。如果我们要从结构中删除一个类型 $X$ 的项，并以某种方式标记现在空的位置，我们就会得到一个带标记孔的结构。结果被称为“单孔上下文”，将类型 $X$ 的项插入孔中，就会得到一个完全填充的 ${\mathit {Tree}}\,X$。这个孔充当一个特殊的位置，一个焦点。这些图说明了这一点。

从 ${\mathit {Tree}}\,X$ 中删除一个类型为 $X$ 的值会在该位置留下一个空洞。

将 $X$ 插入到一个单洞上下文中，这是一个更抽象的图示。

当然，我们感兴趣的是给出单洞上下文类型的类型，也就是如何在 Haskell 中表示它。问题是如何有效地标记焦点。但正如我们即将看到，通过对我们想要获取单洞上下文的类型的结构进行归纳来寻找单洞上下文的表示方法，会自动导致高效的数据类型。因此，给定一个数据结构 $F\,X$，它有一个函子 $F$ 和一个参数类型 $X$，我们想要根据 $F$ 的结构计算单洞上下文的类型 $\partial F\,X$。正如我们选择的符号 $\partial F$ 已经揭示的那样，构造和、积和复合的单洞上下文的规则与莱布尼兹微分规则完全相同。

单洞上下文		图示
$(\partial {\mathit {Const_{A}}})\,X$	$=\,0$	在 $A={\mathit {Const_{A}}}\,X$ 中没有 $X$，因此它的单洞上下文的类型必须为空。
$(\partial {\mathit {Id}})\,X$	$=\,1$	在 $X={\mathit {Id}}\,X$ 中，$X$ 只有一个位置。删除一个 $X$ 不会在结果中留下任何 $X$。由于只有一个位置可以删除它，因此 ${\mathit {Id}}\,X$ 只有一个单洞上下文。因此，单洞上下文的类型是单例类型。
$\partial (F+G)$	$=\partial F+\partial G$	作为 $F+G$ 类型的一个元素，它要么是 $F$ 类型，要么是 $G$ 类型，一个单孔上下文也要么是 $\partial F$ 要么是 $\partial G$.
$\partial (F\times G)$	$=F\times \partial G+\partial F\times G$	一对中的单孔上下文的孔要么在第一个分量中，要么在第二个分量中。
$\partial (F\circ G)$	$=(\partial F\circ G)\times \partial G$	链式法则。组合中的孔是通过在封闭结构中创建一个孔，并将封闭结构填进去而产生的。

当然，填充孔的函数 plug 的类型是 $(\partial F\,X)\times X\to F\,X$.

到目前为止，语法 $\partial$ 表示函子的微分，即一种具有一个参数的类型函数。但还有一种方便的表达式导向符号 $\partial _{X}$ 更适合计算。下标表示我们要对其进行微分的变量。一般来说，我们有

$(\partial F)\,X=\partial _{X}(F\,X)$

一个例子是

$\partial ({\mathit {Id}}\times {\mathit {Id}})\,X=\partial _{X}(X\times X)=1\times X+X\times 1\cong 2\times X$

当然，$\partial _{X}$ 只是逐点式的，而 $\partial$ 是无点式。

练习
将一些规则改写成逐点式。例如，乘积法则的左边变成 $\partial _{X}(F\,X\times G\,X)=\dots$. 为了熟悉单孔上下文，对乘积 $X^{n}:=X\times X\times \dots \times X$ （正好有 $n$ 个因子）进行形式上的求导，并 убедите себя，结果确实对应于相应的单孔上下文。 当然，如果我们不能将类型 $X$ 的值代入单孔上下文，那么它们将毫无用处。写出对应于五个规则的 plug 函数。 为两个变量制定链式法则，并证明它会产生单孔上下文。你可以将双函子 $F\,X\,Y$ 看作是配对 $(X,Y)$ 中的普通函子。当然，你可能需要一个方便的符号来表示双函子的无点式偏导数。

通过求导实现拉链

上面的规则使我们能够为递归数据类型 $\mu F:=\mu X.\,F\,X$（其中 $F$ 是一个多项式函子）构建拉链。拉链是对大型树中特定子树（即类型为 $\mu F$ 的子结构）的关注点。就像上一章一样，它可以用我们想要关注的子树和线程来表示，也就是子树所在的上下文。

${\mathit {Zipper}}_{F}=\mu F\times {\mathit {Context}}_{F}$.

现在，上下文是一系列步骤，每一步都会选择 $F\,\mu F$ 中的特定子树 $\mu F$。因此，未选择的子树由单孔上下文 $\partial F\,(\mu F)$ 收集在一起。这个上下文的孔来自移除我们选择进入的子树。将这些内容放在一起，我们得到

${\mathit {Context}}_{F}={\mathit {List}}\,(\partial F\,(\mu F))$.

或者等效地

${\mathit {Context}}_{F}=1+\partial F\,(\mu F)\times {\mathit {Context}}_{F}$.

为了说明具体的计算过程，让我们系统地构建迷宫数据类型的拉链。

data Node a = DeadEnd a
            | Passage a (Node a)
            | Fork a (Node a) (Node a)

这种递归类型是不动点

${\mathit {Node}}\,A=\mu X.\,{\mathit {NodeF}}_{A}\,X$

函子的

${\mathit {NodeF}}_{A}\,X=A+A\times X+A\times X\times X$.

换句话说，我们有

${\mathit {Node}}\,A\cong {\mathit {NodeF}}_{A}\,({\mathit {Node}}\,A)\cong A+A\times {\mathit {Node}}\,A+A\times {\mathit {Node}}\,A\times {\mathit {Node}}\,A$.

导数为

$\partial _{X}({\mathit {NodeF}}_{A}\,X)\cong A+2\times A\times X$

我们得到

$\partial {\mathit {NodeF}}_{A}\,({\mathit {Node}}\,A)\cong A+2\times A\times {\mathit {Node}}\,A$.

因此，上下文为

${\mathit {Context}}_{\mathit {NodeF}}\cong {\mathit {List}}\,(\partial {\mathit {NodeF}}_{A}\,({\mathit {Node}}\,A))\cong {\mathit {List}}\,(A+2\times A\times ({\mathit {Node}}\,A))$.

与

data Branch a  = KeepStraightOn a
               | TurnLeft  a (Node a)
               | TurnRight a (Node a)
type Thread a  = [Branch a]

比较，我们看到两者完全相同，正如预期的那样！

练习
使用微分，为三叉树重新构建拉链。 构建一个列表的拉链。 关于之前练习的修辞问题：列表和栈有什么区别？

不动点的微分

数据类型不仅仅只有和与积，我们还有固定点运算符，它在微积分中没有直接对应关系。因此，表格中缺少一个微分规则，即如何对固定点进行微分 $\mu F\,X=\mu Y.\,F\,X\,Y$

$\partial _{X}(\mu F\,X)={?}$.

由于其公式涉及到两个变量的链式法则，我们将它留给练习。相反，我们将针对我们具体的示例类型 ${\mathit {Node}}\,A$ 进行计算。

${\begin{matrix}\partial _{A}({\mathit {Node}}\,A)&=&\partial _{A}(A+A\times {\mathit {Node}}\,A+A\times {\mathit {Node}}\,A\times {\mathit {Node}}\,A)\\&\cong &1+{\mathit {Node}}\,A+{\mathit {Node}}\,A\times {\mathit {Node}}\,A\\&&+\partial _{A}({\mathit {Node}}\,A)\times (A+2\times A\times {\mathit {Node}}\,A).\end{matrix}}$

当然，进一步展开 $\partial _{A}({\mathit {Node}}\,A)$ 是无用的，但我们可以将其视为一个固定点方程，从而得到

$\partial _{A}({\mathit {Node}}\,A)=\mu X.\,T\,A+S\,A\times X$

其中缩写为

$T\,A=1+{\mathit {Node}}\,A+{\mathit {Node}}\,A\times {\mathit {Node}}\,A$

以及

$S\,A=A+2\times A\times {\mathit {Node}}\,A$.

递归类型类似于元素类型为 $S\,A$ 的列表，只是空列表被类型为 $T\,A$ 的基本情况取代了。但鉴于列表是有限的，我们可以将基本情况替换为 $1$，并将 $T\,A$ 从列表中拉出来。

$\partial _{A}({\mathit {Node}}\,A)\cong T\,A\times (\mu X.\,1+S\,A\times X)=T\,A\times {\mathit {List}}\,(S\,A)$.

与我们在上一段推导出的拉链进行比较，我们发现列表类型是我们的上下文

${\mathit {List}}\,(S\,A)\cong {\mathit {Context}}_{\mathit {NodeF}}$

以及

$A\times T\,A\cong {\mathit {Node}}\,A$.

最后，我们有

${\mathit {Zipper}}_{\mathit {NodeF}}\cong \partial _{A}({\mathit {Node}}\,A)\times A$.

因此，对我们的具体示例 ${\mathit {Node}}\,A$ 相对于 $A$ 进行微分，会得到一个直到 $A$ 的拉链！

练习
使用二元链式法则，为不动点的微分建立一个规则。 也许您知道存在归纳的不动点 ($\mu$) 和共归的不动点 ($\nu$)。共归的不动点的规则是什么？

关于参数函数的微分

在查找单孔上下文的类型时，我们进行 d f(x)/d x。完全可以求解 d f(x)/d g(x) 之类的表达式。例如，求解 d x^4 / d x^2 得到 2x^2，即一个 4 元组的二孔上下文。推导过程如下：设 u=x^2 d x^4 / d x^2 = d u^2 /d u = 2u = 2 x^2。

拉链与上下文

然而，一般而言，拉链和单孔上下文表示不同的东西。拉链关注任意子树，而单孔上下文只能关注类型构造函数的参数。例如，数据类型

 data Tree a = Leaf a | Bin (Tree a) (Tree a)

是

${\mathit {Tree}}\,A=\mu X.\,A+X\times X$.

拉链可以关注顶端为 Bin 或 Leaf 的子树，但 ${\mathit {Tree}}\,A$ 的单孔上下文的孔，只能关注 Leaf，因为这是 $A$ 类型项所在的地方。 ${\mathit {Node}}\,A$ 的导数之所以恰好是拉链，是因为每个子树的顶端总是用 $A$ 进行修饰。

练习
令人惊讶的是，$\partial _{A}({\mathit {Tree}}\,A)\times A$ 和 ${\mathit {Tree}}\,A$ 的拉链，再次证明是相同的类型。进行计算并不困难，但您能解释一下为什么会出现这种情况吗？ 证明$\mu F$ 的拉链构造可以通过引入辅助变量$Y$，对$\mu X.\,Y\times F\,X$ 求导，然后重新代入$Y=1$。为什么这样有效？ 找到一个类型$G\,A$，其拉链不同于单孔上下文。

结论

我们以一个问题来结束本节：微积分中的规则是如何出现在离散环境中的？目前，没有人知道。但至少，存在一个离散的“线性”概念，即“恰好一次”。将类型$X$ 的项插入单孔上下文的孔中的函数的关键特征是该项恰好使用一次，即线性。我们可以将插入映射视为具有类型

$\partial _{X}F\,X\to (X\multimap F\,X)$

其中$A\multimap B$ 表示线性函数，即不会复制或忽略其参数的函数，如线性逻辑中所述。从某种意义上说，单孔上下文是函数空间$X\multimap F\,X$ 的表示，可以认为是对$X\to F\,X$ 的线性逼近。

另请参阅

• 拉链 在 haskell.org wiki 上
• 通用拉链及其应用
• 基于拉链的文件服务器/操作系统
• Scrap Your Zippers: A Generic Zipper for Heterogeneous Types