高中化学/量子数

我们在这章中花了大量时间谈论波，特别是电子波。虽然大多数人都知道普通水波是什么样子的，但很少有人了解电子波是什么样子的。在上一课中，我们谈论了电子密度，以及如何将电子波看作表示原子中任何空间点电子密度“雾”的厚度或薄度。我们考虑了氢原子中电子的概率模式。现在让我们考虑一些更复杂的原子。

课程目标

• 解释主量子数 n 的含义。
• 解释方位量子数 ℓ 的含义。
• 解释磁量子数 m_l 的含义。

薛定谔方程提供了三个整数，用于定义电子的能量状态和轨道

你应该记得，当电子被困在原子中时，它们会形成驻波。你应该还记得，在任何受限空间中，只允许存在某些驻波，因为只有某些驻波可以完美地适应该空间（记住，完美拟合要求波从盒子开始和结束的地方开始和结束）。在一个一维盒子中，很容易想象所有可以完美地适应盒子的波。在三维空间中，情况稍微复杂一些。不幸的是，当涉及原子中的电子时，除了电子波是三维的这一事实之外，还有一个额外的复杂性！事实证明，原子中的电子并不局限于漂亮的正方形或矩形盒子。相反，它们被限制在球形盒子中（这应该是有道理的，因为原子毕竟是微小的球体）。换句话说，原子内的电子波必须在球体的表面开始和结束。你可能拥有非常好的想象力，并且能够惊人地将物体描绘成三维空间，但对于大多数人来说，试图弄清楚这些球形三维波是什么样子可能是一个不小的挑战。

幸运的是，这就是电子波函数可以提供帮助的地方。电子波函数基本上描述了电子波可以采取的可能形状。我们不会真正担心波函数。相反，我们只会担心特定的数字，称为量子数。量子数始终是电子波函数的一部分，并且在确定概率模式的形状方面非常重要。

当电子波函数首次由一位名叫埃尔温·薛定谔（图 6.11）的人开发时，他的目标是展示如何使用电子的波状描述来理解电子在氢原子中的行为。为了做到这一点，薛定谔首先定义了氢原子本身的大小和球形形状。然后，薛定谔假设被困在氢原子中的电子形成了一个驻波，该驻波完美地适应了原子内部，没有“溢出”或“重叠”自身（事实证明，在圆形或球形盒子中，不匹配的波不会“溢出”那么多，而是“重叠”，如图 6.12 所示。最后，薛定谔假设电子波必须是连续的（记住，连续的东西没有间隙、空洞或跳跃）。

图 6.12：当波在圆形（或球形）上完美拟合时，它们会与自身相遇并形成一个闭环。然而，当波没有在圆形上完美拟合时，它们最终会自身“重叠”。

令人惊讶的是，薛定谔发现，为了满足他对电子波的关于拟合在原子内部和保持连续性的基本假设，电子波函数中的某些量必须是“整数”。每当薛定谔将一个整数分配给这些量时，他最终都会得到一个完美地适应氢原子的波。然而，每当他将一个小数分配给这些量时，他最终都会得到一个波函数，该函数要么“自身重叠”，要么是不连续的！必须分配整数的量很快就被称为量子数。在氢电子波函数中，始终存在三个量子数。第一个量子数 n 称为主量子数，第二个量子数 ℓ 称为方位量子数，第三个量子数 m_l 称为磁量子数。这三个量子数共同定义了电子的能量状态和轨道，但我们将在下一节中详细讨论它们的含义。

n = 主量子数（能级）

第一个量子数，称为主量子数，用符号 n 表示。为了描述一个有效的驻波，n 必须具有整数值，但对 n 还有额外的限制。n 的值必须是正整数值（n = 1, 2, 3, . . .）。换句话说，n 永远不能等于负整数。事实上，n 甚至不能等于 0！主量子数为你提供了关于电子波是什么样的两个不同的线索。首先，它告诉你当你远离原子的中心时，电子密度是如何扩散的。对于具有较低主量子数的电子波，例如 n = 1，电子密度在靠近原子中心的区域非常厚，然后随着你向外移动，它会迅速变薄。相反，对于具有较高主量子数的电子波，例如 n = 6，电子密度在原子中心的区域并不那么厚，而是向外扩散得更远。一般来说，主量子数越高，你就能检测到大量电子密度的距离就越远离原子核（图 6.13）。

当主量子数 n 很小时，大部分电子密度位于靠近原子核的地方。

但是，当主量子数很大时，电子密度会扩散得更远。

图 6.13

有时，你会听到人们说主量子数决定了电子波函数的“大小”。当人们这样说时，他们实际上并不意味着电子波的绝对或总“大小”。他们指的是根据大部分（通常约 90%）的电子密度集中在哪里，电子波看起来有多大或多小。在具有较低主量子数的电子波中，电子密度主要集中在靠近原子中心的区域。即使在远离原子核的距离处存在少量的电子密度，但数量如此之少，你几乎无法察觉到它。结果，具有较低主量子数的电子波看起来很小。另一方面，在具有较高主量子数的电子波中，电子密度扩散得更远，因此在远离原子中心的距离处也更厚。因此，具有较高主量子数的电子波看起来很大。

主量子数还描述了电子波包含的节点总数。什么是节点？节点是电子波绝对没有振幅或“高度”的地方。看看下面的图中的一维波。你能找到节点（部分 a.）吗？现在看看二维波（部分 b.）。你能找到节点吗？一个包含节点的三维波就像洋葱一样。想想洋葱是如何分层的，以及在不同层之间始终存在空隙或断裂。如果洋葱是一个三维波，那么洋葱层之间的断裂就像节点一样。主量子数 n 越高，电子波包含的节点就越多。

节点是波振幅或高度为零的任何地方。a. 和 b. 都说明了表示波的不同方式。在 a. 中，振幅对应于黄色线在黑色轴上方（或下方）的高度。当黄色波与黑色轴交叉时，波的振幅为零，因此存在节点。在 b. 中，波的振幅对应于蓝色云的厚度。当没有蓝色云时，波的振幅为零，因此存在节点。

主量子数极其重要，不仅因为它告诉你有关电子波的“大小”和电子波中的节点数量的信息，而且还因为它告诉你有关该波能量的信息。如果你回忆一下，你会记得负电子喜欢靠近正原子核，因为电子离正电荷越近，能量就越低。这在主量子数方面意味着什么？这意味着，具有较低主量子数的电子波，以及靠近原子核的电子密度，将具有较低的能量，而具有较高主量子数的电子波，以及远离原子核的电子密度，将具有较高的能量。

类似地，随着电子波中节点数量的增加，波的能量也会增加。想想跳绳实验。你还记得你如何在跳绳中制造驻波吗？你需要更多还是更少的能量才能让多条波在绳子上形成？你应该需要更多的能量才能制造更多波。这是因为在制造更多波的过程中，你同时也制造了更多节点，而节点总是与能量增加相关联。再次，让我们看看这在主量子数方面意味着什么。一个具有较低主量子数的电子波具有较少的节点，因此也将具有较低的能量。另一方面，一个具有较高主量子数的电子波具有更多的节点，因此将具有较高的能量。

请注意，随着n的增加，电子波的“大小”和节点数量也随之增加。因此，电子波的能量总是随着n的增加而增加。

1. n的值越大，能量越高。
2. n的值越小，能量越低。

由于主量子数决定了特定电子波的能量，因此n通常被认为是指电子的“能级”。“能级”这个词实际上来自玻尔的原子旧太阳系模型。然而，由于薛定谔及其波动方程，我们现在知道能级并不对应于原子核周围的特定轨道，而是对应于电子被困在原子内部时所采用的特定电子波。

角动量量子数（能级，s，p，d，f）（s=锐，p=主，d=弥散和f=基态）

第二个量子数，称为方位量子数，用符号ℓ表示。虽然主量子数告诉您电子波的“大小”和电子波中节点的数量，但方位量子数告诉您更多关于电子波的“形状”的信息。换句话说，由于电子密度在一个地方比另一个地方“更厚”，电子波所呈现的形状。您可能倾向于认为电子波的形状总是球形的，因为原子本身是球形的。然而，事实证明，虽然存在球形电子波，但也有看起来像哑铃的波，以及看起来像蝴蝶的波，以及看起来如此疯狂以至于几乎无法描述的波！下图显示了一些电子波的不同可能形状。

您可能想知道上面各种气球状形状。使用图纸来表示电子波的一个困难是，电子密度本身实际上是散布在原子中心周围的巨大空间区域。正如您之前所学到的那样，然而，对于许多电子波来说，几乎所有电子密度都靠近原子的原子核，只有极少量的电子密度在更远的地方。多年来，科学家已经开发出一种绘制电子波的标准方法。科学家通常不会尝试解释电子波中所有电子密度，而是只绘制围绕包含约 90% 电子波总电子密度的空间区域的“气球”。下图显示了科学家如何将电子密度云转换为气球。即使在卡通气球之外存在少量的电子密度（因此在气球之外找到电子的概率很小），大多数电子行为可以通过忽略卡通气球无法捕获的少量电子密度来理解。

代表电子波的卡通气球的精确形状由ℓ的值决定。换句话说，上面图像中的哑铃形气球有一个ℓ值，而蝴蝶形气球有另一个ℓ值。当然，科学家会厌倦说“哑铃形波”或“蝴蝶形波”之类的话，因此，他们使用字母表中的字母来命名不同的波。最常见的波形称为s，p，d和f。（如果您对不同的波形看起来像什么有更直观的记忆，科学家可能会给它们起一些很好的描述性名称，例如“哑铃波”或“蝴蝶波”，但这比s，p，d和f这样的枯燥名称更容易记住，但事实证明，这样的枯燥名称更方便）。

在下一课中，我们将更仔细地研究一些常见的波形。首先，我们必须考虑n和ℓ之间的关系。请记住，电子的波函数总是具有三个量子数。因此，为了完全描述电子波，您必须知道所有三个数字的值（n，ℓ和m_l）。现在您可能会认为，只要n，ℓ和m_l都是整数，它们所描述的波就会是一个非常好的电子波。但这不是它的工作方式。事实证明，对于特定的n值，只允许某些ℓ值。

对于实际上描述原子中电子的波函数，ℓ永远不小于 0，但也不大于n − 1（ℓ = 0, 1, 2, … n − 1）。以下示例将有助于澄清对ℓ的限制。

示例 1 对于n = 3 的电子波，ℓ的允许值是多少？ 解决方案: n = 3 1. 找到ℓ的最小值。 ℓ的最小值始终为 0。 2. 找到ℓ的最大值。 ℓ的最大值始终为n – 1 最大ℓ = n − 1 最大ℓ = 3 − 1 最大ℓ = 2 3. 列出从ℓ的最小值开始到ℓ的最大值结束的所有整数（没有小数！） ℓ = 0, 1, 2

示例 2 对于n = 1 的电子波，ℓ的允许值是多少？ 解决方案: n = 1 1. 找到ℓ的最小值。 ℓ的最小值始终为 0。 2. 找到ℓ的最大值。 ℓ的最大值始终为n − 1 最大ℓ = n − 1 最大ℓ = 0 3. 列出从ℓ的最小值开始到ℓ的最大值结束的所有整数（没有小数！） ℓ = 0

通常，科学家会将不同的ℓ值称为电子能级。在只有一个电子的氢原子中，ℓ的值对电子的能量没有影响。然而，在具有多个电子的原子中，ℓ的值确实对电子的能量有微小的影响。换句话说，主量子数n始终决定电子的总体能级，但该能级实际上根据ℓ的值被分成多个能级。所有这些能级在氢原子中具有相同的能量，因为氢原子只有一个电子。然而，对于具有多个电子的原子，不同的能级会分开，其中一些能级最终会比其他能级具有更多的能量。

m_l = 磁量子数（识别轨道）

第三个也是最后一个量子数，称为磁量子数，用符号m_l表示。请记住，主量子数告诉您电子波的“大小”和电子波中节点的数量，而方位量子数告诉您更多关于电子波的“形状”的信息。然而，磁量子数为您提供了更多关于电子波看起来像什么的信息。磁量子数告诉您电子波在空间中的方向。

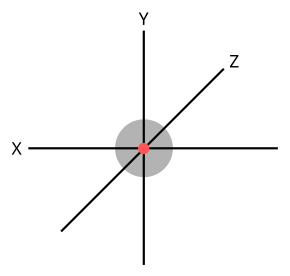
空间方向基本上是指电子波指向哪里。看看图 6.14 中显示的两个哑铃形电子波（在下一课中，您将了解到这些实际上是p轨道）。在第一个电子波中，波的叶瓣沿z轴“上下”指向，而在第二个电子波中，波的叶瓣沿x轴“进出”指向。这两个电子波在空间中的方向不同，因此m_l量子数的值也不同。

图 6.14：具有哑铃形状的电子波的两种可能方向。

现在将图 6.14 与图 6.15 进行比较。在这两个图中，电子波在空间中的方向不同，如红色箭头所示。但是，您注意到图 6.15 中电子波的方向有什么不同？它们看起来一样，不是吗？显然，对于球形电子波，方向并不重要。换句话说，因为球形电子波无论您如何旋转它看起来都一样，所以实际上只有一种方向。那么，一个具有球形形状的电子波应该有多少个不同的 ml 值（记住，m_l 值用于描述方向）？显然，具有球形形状的电子波应该只有一个 ml 值，因为它只有一种可能的方向。那么，具有哑铃形状的轨道呢？它应该有一个单独的 m_l 值，还是应该有几个不同的 ml 值？好吧，由于哑铃形波的不同方向实际上看起来不同，所以您可能希望哑铃形波有几个不同的 m_l 值，每个可能的方向对应一个值。事实上，哑铃形波实际上有三个可能的 m_l 值，因此它有三个可能的方向。（别担心为什么哑铃形波只有正好三个方向。我们将在下一课中稍微讨论一下，但完整的解释需要大量的数学知识，如果您决定学习量子物理学或量子化学，您将学习这些知识）。希望通过比较图 14 和 15，您应该相信波的形状（取决于ℓ）在确定可能方向的数量（或可能 m_l 值的数量）方面很重要。那么，对于给定的ℓ 值，如果您想得到一个有意义的、实际描述氢原子中电子的波函数，只有某些 ml 值是允许的就不足为奇了。

图 6.15：具有球形形状的电子波的两种可能方向。请注意，这些方向之间没有明显的区别。

对于ℓ 的特定值，只有 m_l 的某些值是允许的。

m_l 的规则是，对于任何ℓ 值，m_l 可以是任何从 −ℓ 开始到 +ℓ 结束的整数。m_l = −ℓ … +ℓ')。以下示例应该有助于阐明对 m_l 的限制。

示例 3 对于一个 ℓ = 2 的电子波，ml 的允许值是多少？ 解决方案: ℓ = 2 1. 找到 ml 的最小值。 ml 的最小值始终为 −ℓ。 最小 ml = −2 2. 找到 ml 的最大值。 ml 的最大值始终为 +ℓ 最大 ml = +2 3. 列出所有整数（不包括小数！），从 ml 的最小值开始，到 ml 的最大值结束。 ml = −2, −1, 0, 1, 2

示例 4 对于一个 ℓ = 0 的电子波，ml 的允许值是多少？ 解决方案: ℓ = 0 1. 找到 ml 的最小值。 ml 的最小值始终为 −ℓ。 最小 ml = 0 2. 找到 ml 的最大值。 ml 的最大值始终为 +ℓ 最大 ml = 0 3. 列出所有整数（不包括小数！），从 ml 的最小值开始，到 ml 的最大值结束。 ml = 0

现在我们已经讨论了所有三种不同的量子数，您应该对如何描述不同的电子波有了很好的理解。您可以使用主量子数 n 来描述电子波的“大小”和电子波中节点的数量。您可以使用方位量子数 ℓ 来描述电子波的形状。最后，您可以使用磁量子数 m_l 来描述电子波的方向。既然您知道如何描述一个通用的电子波，那么现在该看看一些特定电子波的示例了。这将是我们下一课要讨论的内容。

课程总结

• 薛定谔发现，为了使波函数描述一个连续的驻波，并且不会“反折”自身，波函数中的某些量必须具有整数值。
• 波函数中必须具有整数值的量称为量子数。
• 在氢的波函数中，有三个量子数。它们被称为主量子数 (n)、方位量子数 (ℓ) 和磁量子数 (m_l)。
• 主量子数只能取正整数值，(n = 1, 2, 3 …)。
• 主量子数决定了电子密度的大部分距离原子中心有多远。n 的值越高，您在原子核更远的地方检测到大量的电子密度的可能性就越大。
• 主量子数还决定了电子驻波中节点的数量。n 的值越高，电子波中的节点就越多。
• 主量子数越高，电子的能量就越大。因此，主量子数决定了电子的能级。
• 方位量子数 ℓ 决定了电子波的形状。ℓ 的值也称为电子能级。它们用字母 s、p、d、f、g、h 等表示。
• 对于实际上描述原子中电子的波函数，ℓ 始终不小于零，但也不大于 n − 1 (ℓ = 0, 1, 2 … n − 1)。
• 在具有多个电子的原子中，ℓ 对电子的能量有轻微的影响。
• 磁量子数 m_l 决定了电子波在空间中的方向。对于给定的 ℓ 值，m_l 可以是任何从 −ℓ 到 + ℓ 的整数 (m_l = −ℓ … +ℓ)。

1. 将每个量子数与它们描述的性质相匹配。

   (a) n	i. 形状
   (b) ℓ	ii. 空间方向
   (c) ml	iii. 节点数量

2. 电子波中电子密度为零的点称为_________。
3. 在以下语句中选择正确的词语。

   (a) n 的值(越高/越低)，电子驻波中的节点就越多。

   (b) n 的值(越高/越低)，电子的能量就越低。

   (c) 电子的能量(越高/越低)，其电子驻波中的节点就越多。

4. 填空。对于较低的 n 值，电子密度通常位于原子核的________，而对于较高的 n 值，电子密度通常位于原子核的________。
5. 圈出所有有意义的语句：薛定谔发现电子波方程中某些量必须是整数，因为当它们不是整数时，波方程描述的波...

   (a) 不连续

   (b) 太小

   (c) 太长太窄

   (d) 太短太胖

   (e) “反折”自身

6. 对于 n = 4 的电子驻波，ℓ 的允许值是多少？
7. 对于 n = 9 的电子驻波，ℓ 可能有多少个值？
8. 对于 ℓ = 3 的电子驻波，ml 的允许值是多少？
9. 对于 ℓ = 4 的电子驻波，可能有多少个不同的方向？
10. 对于 n = 2，m_l 的允许值是多少？

词汇表

方位量子数 (ℓ)

定义电子能级，并决定电子波的形状。

磁量子数 (m_l)

决定电子驻波在空间中的方向。

节点

电子波高度为零的地方。换句话说，它是没有电子密度的。

主量子数 (n)

定义电子的波函数的能级、电子的驻波的大小以及波中的节点数量。

量子数

分配给电子波函数中某些量的整数。因为电子驻波必须是连续的并且不能“反折”自身，所以量子数被限制为整数值。

此材料改编自可以在这里找到的原始 CK-12 书籍 here。这项工作是在知识共享署名 - 相同方式共享 3.0 美国许可下授权的