高中三角学/直角三角形三角学应用

在本课中，我们将回到直角三角形三角学。许多现实情况都涉及直角三角形。在你之前学习几何时，你可能已经使用直角三角形来解决涉及距离的问题，使用勾股定理。在本课中，你将使用你对角度和三角函数的知识，解决涉及直角三角形的问题。我们将首先解决直角三角形，这意味着要确定所有三个角的度数以及直角三角形所有三条边的长度。然后我们将转向几种类型的问题。

学习目标

解直角三角形。
解决需要你解直角三角形的现实世界问题。

解直角三角形

你可以使用你对勾股定理和六个三角函数的知识来解直角三角形。因为直角三角形是一个带有 90 度角的三角形，所以解直角三角形需要你找到另外一个或两个角的度数。你如何解决将取决于提供的信息量。以下示例展示了两种情况：一个缺少一条边的三角形，以及一个缺少两条边的三角形。

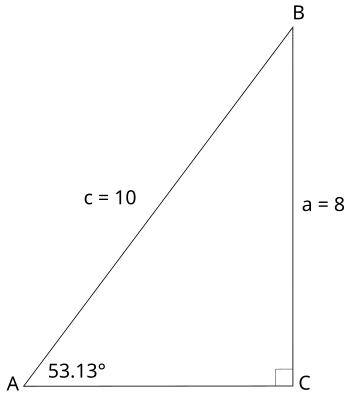
示例 1

解下图所示的三角形。

解答:

我们需要找到所有边的长度和所有角的度数。在这个三角形中，给出了三条边中的两条。我们可以使用勾股定理找到第三边的长度

$8^{2}+b^{2}=\,\!$	$10^{2}\,\!$
$64+b^{2}=\,\!$	$100\,\!$
$b^{2}=\,\!$	$36\,\!$
$b=\,\!$	$\pm 6\Rightarrow b=6\,\!$

(你可能也认识到“勾股定理三元组”，6、8、10，而不是执行勾股定理本身。)

你也可以使用三角比找到第三边。注意，缺失的边，b，与角A相邻，斜边已知。因此，我们可以使用余弦函数来找到b的长度

$\cos(53.13^{\circ })=\,\!$	${\frac {\text{adjacent side}}{\text{hypotenuse}}}={\frac {b}{10}}$
$0.6=\,\!$	${\frac {b}{10}}$
$b=\,\!$	$0.6(10)=6\,\!$

我们也可以使用正切函数，因为给出的是对边。你可能觉得用多种方法来找到缺失的边很混乱。然而，重点不是制造混乱，而是表明你必须查看哪些信息是缺失的，并选择一种策略。总的来说，当你需要识别三角形的一条边时，你可以使用勾股定理，或者使用三角比。

为了解决上述三角形，我们还需要确定所有三个角的度数。已知两个角：90 度和 53.13 度。我们可以使用三角形内角和公式来找到第三个角。

180 − 90 − 53.13 = 36.87°

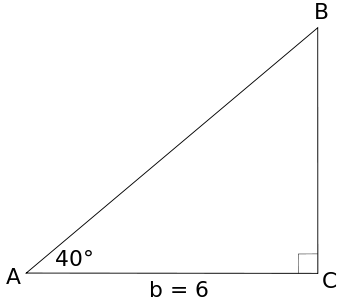
现在让我们考虑一个有两个边缺失的三角形。

示例 2

解下图所示的三角形。

解：在这个三角形中，我们需要找到两条边的长度。我们可以使用三角函数比来找到一条边的长度。然后，我们可以使用三角函数比或勾股定理来找到第三条边的长度。

我们已知角 A 的度数以及与角 A 相邻的边的长度。如果我们要找到斜边的长度 c，我们可以使用余弦比

$\cos(40^{\circ })=\,\!$	${\frac {\text{adjacent}}{\text{hypotenuse}}}={\frac {6}{c}}$
$\cos(40^{\circ })=\,\!$	${\frac {6}{c}}$
$c\cos(40^{\circ })=\,\!$	$6\,\!$
$c=\,\!$	${\frac {6}{\cos(40^{\circ })}}\approx 7.83$

如果我们要找到三角形另一条边的长度，我们可以使用正切比。（为什么这比使用正弦比更好？）

$\tan(40^{\circ })=\,\!$	${\frac {\text{opposite}}{\text{adjacent}}}={\frac {a}{6}}$
$\tan(40^{\circ })=\,\!$	${\frac {a}{6}}$
$a=\,\!$	$6\tan(40^{\circ })\approx 5.03\,\!$

现在我们知道这个三角形所有三条边的长度。在复习问题中，您将使用勾股定理验证 c 和 a 的值。在这里，为了完成三角形的求解，我们只需要找到角 B 的度数。

180 − 90 − 40 = 50°

请注意，在两个示例中，两个非直角中有一个是已知的。如果两个非直角都没有给出，您将需要新的策略来找到角度。您将在第 4 章学习这种策略。

仰角和俯角

如果您知道仰角或俯角，则可以使用直角三角形来找到距离。下图显示了这两种类型的角度。

仰角是水平视线与指向目标的视线之间的夹角。例如，如果您站在地面上向上看山顶，您可以测量仰角。俯角是水平视线与向下指向目标的视线之间的夹角。例如，如果您站在山顶或建筑物上，向下看某个物体，您可以测量俯角。您可以使用测角仪或经纬仪来测量这些角度。人们倾向于使用测角仪或经纬仪来测量树木和其他高大物体的高度。在这里，我们将解决几个涉及这些角度和距离的问题。

示例 3

您站在一棵树 20 英尺远的地方，您测量到的仰角为 38°。这棵树有多高？

解答:

解取决于您的身高，因为您是从视线水平测量仰角的。假设您身高 5 英尺。那么下图显示了您正在解决的三角形。

该图显示，一旦我们找到 T 的值，我们必须将 5 英尺加到这个值才能找到三角形的总高度。为了找到 T，我们应该使用正切值

$\tan(38^{\circ })=\,\!$	${\frac {\text{opposite}}{\text{adjacent}}}={\frac {T}{20}}$
$\tan(38^{\circ })=\,\!$	${\frac {T}{20}}$
$T=\,\!$	$20\tan(38^{\circ })\approx 15.63\,\!$
${\text{Height of tree}}\approx \,\!$	$20.63\ {\text{ft}}\,\!$

下一个例子展示了俯角。

例 4

你站在一栋大楼的顶端，看着远处的一个公园。俯角是 53°。如果你所站的大楼高 100 英尺，公园离你有多远？你的身高有影响吗？

解答:

如果我们忽略人的身高，我们解决下面的三角形

给定俯角为 53°，上图中角度 A 为 37°。我们可以使用正切函数来找到大楼到公园的距离

$\tan(37^{\circ })=\,\!$	${\frac {\text{opposite}}{\text{adjacent}}}={\frac {d}{100}}$
$\tan(37^{\circ })=\,\!$	${\frac {d}{100}}$
$d=\,\!$	$100\tan(37^{\circ })\approx 75.36\ {\text{ft}}\,\!$

如果我们考虑人的身高，这会改变邻边的值。例如，如果这个人高 5 英尺，我们就有不同的三角形

$\tan(37^{\circ })=\,\!$	${\frac {\text{opposite}}{\text{adjacent}}}={\frac {d}{105}}$
$\tan(37^{\circ })=\,\!$	${\frac {d}{105}}$
$d=\,\!$	$105\tan(37^{\circ })\approx 79.12\ {\text{ft}}\,\!$

如果你只是想估计一个距离，那么你可以忽略测量者的身高。但是，在距离或长度较小的场合，测量者的身高会更加重要。例如，在树高问题中，测量者的身高会比在建筑物问题中对结果的影响更大，因为树的高度更接近测量者，而不是建筑物。

直角三角形和方位角

我们也可以使用直角三角形，通过给定的方位角来寻找距离。在航海中，方位角是两个物体之间方向。在航空航海中，方位角是相对于正北方向，顺时针旋转的角度。下图显示了 70 度角

需要注意的是，导航问题中的角度测量方式与单位圆中的角度测量方式不同。此外，导航和测量中的角度也可能用北、东、南、西来表示。例如，N70° E 表示从北向东的角度，而 N70° W 表示从北向西的角度。N70° E 与上图中的角度相同。N70° W 将导致第二象限中的角度。

以下示例展示了如何使用方位角查找距离。

例 5

一艘船以 N50° E 的航线航行。该船航行直到它位于距离其出发港口正东 10 海里的港口正北方向。该船航行了多远？

解答:

与 d 相对的角度是 50° 的余角，即 40°。因此，我们可以使用余弦函数找到 d

$\cos(40^{\circ })=\,\!$	${\frac {\text{adjacent}}{\text{hypotenuse}}}={\frac {10}{d}}$
$\cos(40^{\circ })=\,\!$	${\frac {10}{d}}$
$d\cos(40^{\circ })=\,\!$	$10\,\!$
$d=\,\!$	${\frac {10}{\cos(40^{\circ })}}\approx 13.05\ {\text{nm}}$

直角三角形的其他应用

一般来说，您可以使用三角学来解决任何涉及直角三角形的难题。接下来的几个例子展示了可以使用直角三角形来查找长度或距离的不同情况。

例 6

在第 3 课中，我们介绍了以下情况：您正在建造一个斜坡，以便轮椅使用者可以进入建筑物。如果斜坡必须高 8 英尺，斜坡的角度必须约为 5°，那么斜坡必须多长？

已知我们知道斜坡的角度和与角度相对边的长度，我们可以使用正弦比来查找斜坡的长度，即三角形的斜边

$\sin(5^{\circ })=\,\!$	${\frac {8}{L}}$
$L\sin(5^{\circ })=\,\!$	$8\,\!$
$L=\,\!$	${\frac {8}{\sin(5^{\circ })}}\approx 91.8\ {\text{ft}}$

这看起来可能是一个很长的斜坡，但实际上，5° 的斜坡角度是美国残疾人法案 (ADA) 要求的。这解释了为什么许多斜坡由几个部分组成，或者有转弯。需要额外的距离来弥补小的坡度。

直角三角形三角学也用于测量实际上无法测量的距离。下一个例子展示了月球和太阳之间距离的计算。此计算要求我们知道地球到月球的距离。在第 5 章中，您将学习正弦定理，这是计算地球到月球距离所必需的公式。在以下示例中，我们假设此距离，并使用直角三角形来查找月球和太阳之间的距离。

例 7

地球、月球和太阳在月相为上弦月时形成一个直角三角形。地球到月球的距离约为 240,002.5 英里。太阳和月球之间的距离是多少？

解答:

令 d = 太阳和月球之间的距离。我们可以使用正切函数来求 d 的值

$\tan(89.85^{\circ })=\,\!$	${\frac {d}{240,002.5}}$
$d=\,\!$	$240,002.5\tan(89.85^{\circ })=91,673,992.71\ {\text{miles}}$

因此，太阳和月亮之间的距离远大于地球和月亮之间的距离。

课程总结

在本课中，我们回到了直角三角形三角函数的主题，以解决涉及直角三角形的现实世界问题。为了找到长度或距离，我们使用了仰角、俯角、导航方位角以及其他产生直角三角形的实际情况。在后面的章节中，您将扩展本章的工作：您将学习使用三角函数比找到缺失的角度，并且您将学习如何确定非直角三角形的角度和边。

思考点

在哪些情况下自然会出现直角三角形？
是否存在无法求解的直角三角形？

三角函数可以解决天文尺度上的问题，也可以解决地球上甚至分子或原子尺度上的问题。为什么这是真的？

复习题

求解三角形
两位朋友正在写练习题来为三角函数考试做准备。萨姆为他的朋友安娜写了以下问题来解决
在直角三角形ABC中，角C的度数为90度，边c的长度为8英寸。求解该三角形。

安娜告诉萨姆这个三角形无法求解。萨姆说她错了。谁是对的？解释你的想法。
使用勾股定理来验证例2中三角形的边。
从地面到旗杆顶部的仰角测得为53°。如果测量距离为15英尺，那么旗杆有多高？
从山顶到一座房子的俯角测得为14°。如果山高30英尺，那么房子距离山顶多远？
一架飞机从城市A起飞，以100°的方位角飞行。城市B位于城市A的正南方。当飞机位于城市B的东边200英里时，飞机飞行了多远？城市A和城市B相距多远？
下图所示的现代建筑采用了一个外墙（左侧所示），它与地板不呈90度角。右侧的墙垂直于地板和天花板。

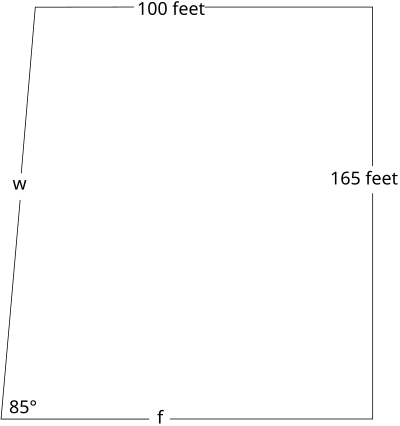
倾斜的外墙w的长度是多少？主地板f的长度是多少？
一位测量员正在测量一个池塘的宽度。她在池塘的另一边选择了一个地标，并测量了从距离原点50英尺的地方到这个地标的角度。池塘有多宽？
求边x的长度