高中三角学/测量旋转

在本课中，您将学习关于旋转角，它们存在于许多不同的现实现象中。例如，考虑一个使用转盘玩的游戏。当你旋转转盘时，它转了多少？

您可以用多种方式回答这个问题。您可以说类似“转盘转了三圈”。这意味着转盘做了三个完整的旋转，然后回到了它开始的位置。

我们也可以用度数来测量旋转。在上一课中，我们处理了三角形中的角度，用度数来测量。您可能还记得几何学中，一个完整的旋转是 360 度，通常写成 360°。那么，半旋转是 180°，四分之一旋转是 90°。这些测量结果在这节课以及本章的其余部分将非常重要。

学习目标

确定一个角是锐角、直角、钝角还是平角。
用度、分和秒表示角度的度数。
用十进制度表示角度的度数。
识别和绘制标准位置的旋转角。
识别象限角。
识别终边相同的角。

锐角、直角、钝角和平角

一般来说，角度按大小分类。下表总结了这些类别，您可能在上一课中已经熟悉。

表 1.8
名称	描述
锐角	度数小于 90 度的角。
直角	度数正好为 90 度的角。
钝角	度数大于 90 度，但小于 180 度的角。
平角	度数正好为 180 度的角。

您应该确保能够直观地确定一个角属于哪个类别。

示例 1

确定该角是锐角、直角、钝角还是平角。

a.

b.

c.

解决方案:

a. 此角是锐角。

如果难以直观地对角度进行分类，您可以将其与直角进行比较。这样做将有助于您看到该角度小于直角。

b. 此角是钝角。

同样，如果需要，您可以将该角度与直角进行比较。

c. 此角是直角。

需要注意的是，直角通常用一个小方块标记。

还需要注意的是，您可以使用量角器来确定一个角的度数。当然，这种测量结果只是一个近似值，因为没有量角器是完美的，测量的人也无法完美地对准量角器或保持其稳定。

示例 2

使用量角器来测量示例 1a 中的角。

解决方案:

该角度约为 50°。

在处理用度数测量的角度时，我们经常使用小数来表示答案，例如 78.5°。但是，在某些情况下，角度是用分数来测量的。

测量角度

示例 3

两个轮子直接接触。一个轮子的半径为 0.5 米，另一个轮子的半径为 1 米。较小的轮子旋转了四圈。较大的轮子旋转了多少圈？较大的轮子旋转了多少度？

解决方案:

每次小轮子旋转一次，它的整个周长都会沿着大轮子移动，C = 2π(.5)。由于大轮子的周长是 2π(1)，所以大轮子旋转了半圈。因此，如果小轮子旋转了 4 圈，即 360 · 4 = 1440°，那么大轮子旋转了 2 圈，即 360 · 2 = 720°。

我们可以用与测量时间相同的方式来测量角度。一分是 ${\tfrac {1}{60}}$ 度。一秒是 ${\tfrac {1}{60}}$ 分，因此它也是 ${\tfrac {1}{360}}$ 度。例如，48°20′45″ 是我们用来表示 48 度、2 分和 45 秒的方式。我们可以用分数记法以及小数记法来表示这个角度

48^{\circ }20'45''=48+{\frac {20}{60}}+{\frac {45}{360}}=48+{\frac {1}{3}}+{\frac {1}{8}}=48{\frac {11}{24}}=48.458{\overline {3}}\approx 48.4583^{\circ }

我们也可以用度、分和秒来表示十进制度。例如，我们可以重新写 125.88°，如果我们将小数部分写成分数

0.88={\frac {88}{100}}={\frac {x}{60}}

现在解出 x

${\frac {88}{100}}=$	${\frac {x}{60}}$
${\frac {44}{50}}=$	${\frac {x}{60}}$
$44\times 60=\,\!$	$50x\,\!$
$2640=\,\!$	$50x\,\!$
$x=\,\!$	$52.8\,\!$

现在我们有 125.88° = 125°52.8′。我们需要将 0.8 分钟转换为秒。

${\frac {0.8}{60}}=$	${\frac {s}{360}}$
$0.8\cdot 360=$	$60x\,\!$
$288=\,\!$	$60s\,\!$
$s=\,\!$	${\frac {288}{60}}$
$s=\,\!$	$4.8\,\!$

所以 125.88° = 125°52′4.8″。

注意，角度 125.88° 是一个钝角。它的度数小于 180°。大于 180° 的角度看起来像什么？大于 360° 呢？

接下来，您将学习一种特定的角度表示方法，使您可以表示 180°、360° 或任何其他角度。

标准位置的旋转角度

我们可以利用我们对绘图的了解来表示任何角度。下图显示了一个处于所谓的标准位置的角度。

标准位置的角度的初始边始终位于正的x轴上。终边始终与初始边在原点处相遇。注意，旋转方向为逆时针。这意味着如果我们顺时针旋转，我们将产生一个负角度。以下是标准位置中几个角度的示例。

90 度角是四个象限角之一。象限角是指其终边位于轴上的角。除了 90° 之外，0°、180° 和 270° 也是象限角。

这些角度被称为象限角，因为每个角度都定义了一个象限。注意，如果没有箭头指示旋转，270° 看起来就像 90°，定义了第四象限。另外注意，360° 看起来就像 0°。区别在于旋转的动作。这个两个角度实际上是同一个角度的想法将在下一节讨论。

同界角

考虑标准位置中的 30° 角。

现在考虑 390° 角。我们可以将这个角度看作是完整的旋转 (360°)，再加上额外的 30 度。

注意，390° 看起来与 30° 相同。形式上，我们说这些角度共享相同的终边。因此，我们称这些角度为同界角。不仅这两个角度是同界角，而且还有无数个与这两个角度同界角的角度。例如，如果我们再旋转 360°，我们就会得到 750° 角。或者，如果我们在负方向 (顺时针) 产生角度，我们就会得到 −330 角。因为我们可以在任一方向旋转，并且可以旋转任意多次，所以我们可以不断地产生与 30° 同界角的角度。

示例 3

哪些角度与 45° 同界角？

a. -45°

b. 405°

c. -315°

d. 135°

解决方案:

b. 405° 和 c. -315° 与 45° 同界角。

注意，第一个角度 −45° 的终边在第四象限。最后一个角度 135° 在第二象限。因此，这两个角度都不与 45° 同界角。

现在考虑 405°。这是一个完整的旋转，再加上额外的 45 度。因此，这个角度与 45° 同界角。−315° 角可以通过顺时针旋转产生。为了确定终边的位置，使用象限角作为标记可能会有所帮助。例如，如果您顺时针旋转 90 度 3 次 (总共 270 度)，则该角度的终边位于正的y轴上。对于总的顺时针旋转 315 度，我们还需要旋转 315 − 270 = 45 度。这使得该角度的终边与 45° 相同。

课程总结

在本课程中，我们根据角度的大小对角度进行了分类，并且扩展了我们对角度的了解，使其包含旋转角度。我们定义了角度处于标准位置的含义，并观察了标准位置中的角度，包括象限角。我们还定义了同界角的概念。本课程中的所有概念都将在下一节中使用，以定义本章的重点内容——三角函数。

需要考虑的点

一个角度如何与另一个角度看起来完全相同？
您在现实生活中在哪里可能看到旋转角度？

复习问题

确定该角是锐角、直角、钝角还是平角。
(a)

(b)
估计该角度的度数。解释您的估计方法。
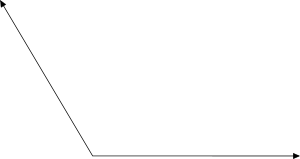
将每个角度的度数、分和秒重写。
(a) 85.5°

(b) 12.15°

(c) 114.96°
将每个角度的度数重写为小数形式。
(a) 54°10'25"

(b) 17°40'5"
确定在给定时间钟表指针之间的夹角大小。
(a) 6:00

(b) 3:00

(c) 1:00
从凌晨 12:00 到凌晨 1:00，钟表的分钟指针旋转了多少角度？
一辆汽车在赛道上行驶，经过了一个 90 度的圆形弯道。汽车轮子的直径为 0.6 米，两个轮子之间的距离为 2 米。汽车行驶的弯道半径为 100 米，以最靠近赛道的一侧的轮子测量。汽车外侧轮子旋转的圈数与内侧轮子旋转的圈数相差多少？
说明一个与 90° 终边相同的角的度数。
说出两个与 120° 终边相同的角。
(a) 一个负角。

(b) 一个大于 360° 的角。
一辆赛车在赛道上经过了一个 180 度的圆形弯道，弯道半径为 120 米。赛车的前后轮直径不同。前轮直径为 0.6 米，后轮直径更大，为 1.8 米。前后轮轴长为 2 米。哪一个轮子在经过弯道时旋转的圈数更多？这个轮子比旋转圈数最少的轮子多旋转了多少度？