高中三角函数/基本函数

本章将向您介绍一个特殊的函数族——三角函数，它是本书的基础。在本第一课中，我们将回顾一般函数的基本特征：什么是函数，函数的图形是什么样的，以及几个函数族的特征。虽然本课不会定义三角函数，但我们将考虑它们的基本特征之一，以及这些函数的一些重要应用。

学习目标

确定一个关系是否为函数。
说明函数的定义域和值域。
根据函数族对函数进行分类。
识别函数的关键特征，包括周期函数的概念。

函数的基础

考虑下面方框中所示的两种情况

情况1：您的汽车以 55 英里/小时的速度行驶，每加仑汽油可以行驶 30 英里。您每增加一英里/小时的速度，汽车每加仑汽油的行驶里程就会减少半英里。

情况2：您从您班上的几位学生那里收集了他们的年龄和身高（英寸）数据

年龄	18	17	18	18	17
身高	65"	64"	67"	68"	66"

在第一种情况下，令变量x表示汽车的速度，令y表示汽车使用一加仑汽油可以行驶的英里数。如果您以x英里/小时的速度行驶，那么您将在一加仑汽油的驱动下行驶y = 30 − .5 (x − 55)英里。例如，如果您以 60 英里/小时的速度行驶，那么您将在一加仑汽油的驱动下行驶 30 − .5(60 − 55) = 27.5 英里。请注意，您可以使用您的速度来“预测”一加仑汽油可以行驶多远。

现在考虑第二种情况。您可以使用这些数据来“预测”身高，前提是知道学生的年龄吗？

在第二种情况下并非如此。例如，如果一名学生 18 岁，那么该学生可能有多种身高。

这两种情况都是关系。关系仅仅是两组数字或数据之间的关系。例如，在第二种情况下，我们通过将每个学生的资料写成有序对，建立了学生年龄和身高之间的关系。在第一种情况下，汽车的速度与其一加仑汽油的使用效率之间存在关系。第一个例子与第二个例子不同，因为它表示一个函数：每个 x 只与一个 y 配对。一些关系在数学上很重要。例如，圆和椭圆是x和y坐标之间重要关系的图形表示，但对于每个x坐标，并非都有唯一的y坐标。由于每个x都有唯一的y，因此函数在数学和科学中发挥着重要作用。

我们可以用多种方式表示函数。一些最常见的表示函数的方式包括：有序对集、方程和图形。下图显示了用每种表示法描绘的函数

表 1.1：函数示例
表示法	示例
有序对集	(1,3), (2,6), (3,9), (4,12)（此函数的有序对子集）
方程	y = 3x
图形	y=3x

相反，下图所示的关系不是函数

表 1.2：非函数示例
表示法	示例
有序对集	(4,2), (4,-2), (9,3), (9,-3)（此函数的有序对子集）
方程	x = y²
图形	x=y^2

为了验证此关系不是函数，我们必须证明至少有一个x值与多个y值配对。如果您查看第一个表示法（有序对集），您可以看到 4 与 2 和 -2 配对。同样，9 与 3 和 -3 配对。因此，该关系不是函数。如果我们查看上面的图形，我们可以看到，除了x = 0之外，关系的x值都与两个y值配对。因此，上述关系不是函数。

快速确定一个关系是否为函数的一种方法是执行垂直线测试，这意味着您在图形上画一条垂直线。例如，如果我们在x = y²的图形上画一条x = 4的线，则该线将与图形相交两次。这意味着该关系不是函数。

示例1

确定关系是否为函数。

a. (2,4), (3,9), (5,11), (5,12)

b.

解答:

a. 此关系不是函数，因为 5 与 11 和 12 配对。如果您绘制这些点，则x = 5的线将与关系中的 2 个点相交。

b. 此关系是函数，因为每个x都只与一个y配对。

一旦您能够确定一个关系是否为函数，那么您应该能够说明定义函数的x值集和y值集。

函数的定义域定义为函数定义的所有x值的集合。例如，函数y = 3x的定义域是所有实数的集合，通常写成 $\mathbb {R}$ 。这意味着x可以是任何实数。其他函数具有受限的定义域。例如，函数 $y={\sqrt {x}}$ 的定义域是所有大于或等于零的实数的集合。此函数的定义域之所以受到限制，是因为负数的平方根不是实数。因此，定义域被限制为非负的x值，以便函数值被定义。

通常可以通过 (1) 考虑可能存在的限制和 (2) 查看图形来轻松确定函数的定义域。

示例2

说明每个函数的定义域。

a. y = x²

b. $y={\tfrac {1}{x}}$

c. (2, 4), (3, 9), (5, 11)

解答:

a. 此函数的定义域是所有实数的集合。没有限制。

b. 此函数的定义域是所有实数的集合，除了 x ≠ 0。定义域之所以受到此限制，是因为分母为零的分数是未定义的。

c. 此函数的定义域是x值的集合 {2, 3, 5}。

变量x通常称为自变量，而变量y通常称为因变量。我们这样谈论x和y，因为函数的y值取决于x值是什么。这就是为什么我们也说“y是x的函数”。例如，函数y = 3x中y的值取决于我们正在考虑的x值。如果x = 4，我们可以很容易地确定y = 3(4) = 12。

当我们使用方程形式的函数时，有一种特殊的符号可以用来强调y是x的函数这一事实。例如，方程y = 3x也可以写成f(x) = 3x。务必记住，f(x)表示y值或函数值，字母f**不是**变量。也就是说，f(x)并不意味着我们将数字f乘以另一个数字x。可以将函数想象成一台机器，它接收一个数字x，并输出另一个数字。在表达式f(x)中，f是机器，括号()是输入x进入机器的地方。f(x)是机器使用输入x产生的输出。例如，假设你的机器对输入加5。那么f(3) = 8，或者更一般地，f(x) = x + 5。

现在我们已经考虑了函数的定义域，我们将转向函数的**值域**，它是函数定义的所有y值的集合。就像我们对定义域所做的那样，我们可以检查一个函数并确定它的值域。同样，考虑可能存在的限制以及函数的图形是什么样子通常很有帮助。例如，考虑函数y = x²。

此函数的值域是所有大于或等于零的实数的集合。这是因为每个y值都是一个x值的平方。如果我们对正数和负数进行平方，结果将始终为正。如果x = 0，则y = 0。如果我们查看y = x²的图形，我们也可以看到值域。

一些函数有突然的跳跃。考虑将数字舍入到最接近的整数的“舍入”函数（如果数字正好位于两个整数之间，则向上舍入）。因此，此函数的一些值为 (2, 2)、(1.4, 1)、(3.9, 4)、(5.5, 6) 和 (−5.5, −5)。此函数的定义域是所有实数，但函数的值域是整数。

另一个跳跃函数来自出租车通常的收费方式。假设出租车前2英里收费5.00美元，然后每增加1英里或部分英里收费1美元。考虑一个函数，其中行驶距离作为输入，出租车费作为输出。因此，此函数的一些值为 (1, 5)、(1.9, 5)、(2.1, 6)、(10, 13)。此函数的定义域是非负实数（因为你不能乘坐出租车行驶负距离）。此函数的值域是所有大于或等于 5 的正整数：{5, 6, 7, 8, ...}。

示例 3

指出函数 $y={\tfrac {2}{x}}$ 的定义域和值域。

解答:

对于此函数，我们可以选择任何x值，除了x ≠ 0。因此，函数的定义域是所有实数的集合，除了x ≠ 0。

值域也限于非零实数，但原因不同。因为分数的分子是2，所以分子永远不可能等于零，因此分数永远不可能等于零。

现在我们已经定义了关系是什么是函数，并且我们已经定义了函数的定义域和值域，我们可以查看一些特定函数及其图形的示例。

函数族

我们迄今为止看到的示例包括几种不同类型的函数。根据您之前使用方程和图形的经验，您可能已经对方程形式与图形外观之间的关系建立了联系。在这里，我们将检查几个函数“族”。函数族是一组方程形式相似的函数。“母函数”是指族中最简单的形式的方程。例如，y = x²是其他函数（如y = 2x² − 5x + 3）的母函数。下表总结了几个函数族的关键方面。

表 1.3：函数族
函数族	母函数	关键方面
线性函数	y = x	线性函数的图形是一条直线，通常根据其斜率和y截距来识别。直线的斜率是系数 ${\tfrac {1}{2}}$ ，y截距是常数 1。
二次函数	y = x²	这些函数的最高指数为 2。图形是抛物线，它有一个顶点，该顶点是图形的全局最大值或最小值。顶点是点 (1, -1)。图形关于直线x = 1 对称。
三次函数	y = x³	这些函数的最高指数为 3。图形的两端具有相反的行为。三次函数的图形要么有一个局部最大值和最小值，如右侧图形所示，要么没有局部最大值或最小值，如y = x³。
指数函数	y = 2^x、y = 3^x 等。	指数函数的指数是变量。图形具有水平渐近线。当x接近 $-\infty$ 时，函数值接近x轴 (y = 0)。
有理函数	$y={\tfrac {1}{x}},$ 等。	这些函数包含分子和分母中都有多项式的分数。图形具有水平和垂直渐近线。当x接近 $\pm \infty$ 时，y值接近 0 (x轴)。当x接近 1 时，y值接近 $\pm \infty$ 。

所有这些函数都可以用来表示真实情况。例如，线性函数y = 3x在上面用于表示你销售每块 3.00 美元的糖果棒能赚多少钱。这种情况称为**正比例关系**。我们说你赚的钱与你卖出的糖果棒的数量成正比。两个变量之间的正比例关系将始终由形式为y = mx的线性函数建模。直线的斜率m是比例常数。请注意，直线的y截距为 0；也就是说，直线包含点 (0, 0)。从卖糖果的角度来看，这是有道理的：如果你卖 0 块糖果棒，你就赚 0 美元。

其他情况可以用不同类型的线性函数建模。考虑以下情况：一家餐厅正在举行促销活动：一个大奶酪比萨饼 8.00 美元，每个配料 2.00 美元。比萨饼的成本可以用函数c(x) = 2x + 8 建模，其中x是比萨饼上的配料数量。直线的斜率为 2，因为每个配料都会使价格增加 2 美元。y截距为 8：如果你不选择任何额外的配料，比萨饼的成本为 8.00 美元。

二次、三次和其他多项式函数可以用来模拟许多类型的情况。另一个重要的函数族是有理函数，或多项式的商，例如

f(x)={\frac {3x}{x^{2}+1}}

f(x)={\frac {1}{x}}

例如，可以使用有理函数来模拟两个变量之间的反比例关系。反比例关系意味着两个变量的乘积是常数：xy = k。如果我们解出此方程以求得y，则有 $y={\tfrac {k}{x}}$ ，这是一个有理函数。以下示例展示了实际情况中的反比例关系

示例 4

有时你开车上班，有时你骑自行车上班。昨天你以平均 40 英里/小时的速度开车，用了 15 分钟。今天你以 20 英里/小时的速度骑自行车，用了半小时。

写出一个方程，表示你的速度和你上班所需时间之间的关系。

解答:

y={\frac {10}{x}}

，其中x 是你的速度（英里/小时），y 是你上班所需的时间（小时）。

首先，请注意家和工作地点之间的距离为 10 英里

{\text{40 miles per hour}}\times {\frac {1}{4}}hr={\text{10 miles}}

{\text{20 miles per hour}}\times {\frac {1}{2}}hr={\text{10 miles}}

我们知道，一般来说

{\text{rate}}\cdot {\text{time}}={\text{distance}}

{\text{time}}={\frac {\text{distance}}{\text{rate}}}

因此，如果你以x 英里/小时的速度开车或骑车，那么你上班需要y 小时： $y={\frac {10}{x}}$ 。

一般来说，函数可以用来模拟许多环境中的真实现象，包括科学、商业、经济等不同领域。可以用来模拟特定情况的函数类型取决于函数的关键方面，这些关键方面将与情况的关键方面相匹配。许多情况的一个方面在我们迄今为止看到的函数类型中没有体现，但将在本章中你将学习到的三角函数中体现。例如，考虑下表，它显示了 1971 年至 2000 年马萨诸塞州波士顿市每月平均最高和最低气温。（来源：rssweather.com）

表 1.4：马萨诸塞州波士顿市的月平均最高/最低气温
月份	最低	最高
一月	22.1°F	36.5°F
二月	24.2°F	38.7°F
三月	31.5°F	46.3°F
四月	40.5°F	56.1°F
五月	50.2°F	66.7°F
六月	59.4°F	76.6°F
七月	65.5°F	82.2°F
八月	64.5°F	80.1°F
九月	56.8°F	72.5°F
十月	46.4°F	61.8°F
十一月	37.9°F	51.8°F
十二月	27.8°F	41.7°F

下图显示了平均低温。

请注意，该图包含一整年的数据，然后以 12 月（第 12 个月）结束。我们有可能用我们讨论过的某个函数族中的函数来近似该图所暗示的曲线。并非所有自然现象都能用数学函数建模，但许多都能。

假设此数据总体上代表了波士顿的天气。我们可以创建一个函数，其输入是从现在开始的月份时间，其输出是预期的平均温度。例如f(1) = 22.1，f(5) = 50.2。该函数将在一年后重复。13 代表什么？根据这些数据，预计气温是多少？

由于月份每年循环，因此 13 代表下一年的 1 月，并且一般来说，我们可以根据我们对某个地点的通常气候的了解来预测 1 月的天气。例如，1 月是波士顿市一年中最冷的月份。在表格所示的年份中，平均低温约为 22 度。因此，我们可以预测波士顿 1 月的平均低温将约为 22 度。我们可以使用这样的函数将当前天气与过去的天气进行比较，并检验随时间推移的气候变化。

由于一年中的月份和天气模式本质上是循环的，因此我们需要用一个本质上也是循环的函数来模拟这种情况。此类函数称为周期性函数。如果存在某个值p，使得对于函数域中的所有x，f(x + p) = f(x)，则该函数是周期性的。你将在本章中学习到的三角函数是一种周期性函数，我们可以使用某些三角函数来模拟上面显示的天气数据。我们将在本课结束时回到这个主题，但现在我们将看看函数的图形。

函数绘图和技术工具

虽然有一些技巧可以让你高效地手绘许多函数的图像，但使用绘图计算器可以让你快速绘制任何函数的图像，并识别函数的关键特征。以下两个例子将向你展示如何使用TI图形计算器来探索函数。

例5

绘制函数y = x³ − 3x² + 1 的图像

a. 当x = 0，x = 2 和 x = −2 时，计算函数值。

b. 描述函数的端点行为。

c. 近似所有x截距。

d. 近似任何局部最大值和最小值。

解答:

要绘制此函数的图像，请按[Y=]，并清除已输入的任何方程。在Y1中，输入方程。如果你以前从未输入过方程，这里有一些提示

x 按钮位于绿色[ALPHA]按钮旁边（在TI-83型号上）。
要将x 提升到3次方，请按[MATH].
要将x 提升到2次方，请按[x²]按钮，该按钮位于左侧列。
小心使用负号：右侧的蓝色“−”按钮用于减法。底部写着“(−)”的按钮用于表示负数。

输入方程后，请按[ZOOM] [6]。这将带你到“标准”窗口：你可以看到从−10到10的x和y。（注意，如果你向下滚动到选项6，则需要按回车键。但是，如果你只输入数字6，则会进入图形。）

a. 要计算函数值，你可以“跟踪”图形。按[TRACE]按钮。你应该在屏幕顶部看到方程，光标应该位于y截距 (0, 1) 上。在屏幕底部，你应该看到x = 0 和y = 1。这告诉我们，对于x = 0，函数值为1。

现在你处于跟踪模式，你可以输入任何x值，计算器将告诉你y值。例如，如果你按下[2] [ENTER]，你会看到光标移动到点 (2,−3)，并且在屏幕底部，你会看到x = 2 和y = −3。如果你按下[(-)] [2] [ENTER]，你将在屏幕底部看到x = −2 和y = −19。请注意，你无法在图形上看到该点。要查看该点，我们需要更改窗口。按[WINDOW]并向下滚动到Ymin。将−10更改为−25。然后按[GRAPH]。现在按[TRACE] [(-)] [2] [ENTER]。你应该看到点(−2,−19)。

b. 端点行为：图形的左侧似乎正在向下，右侧似乎正在向上。如果我们想看到更多图形，我们可以缩小。按[ZOOM] [3]。这将增大窗口的大小。如果你按下[ENTER]，窗口将再次增大。如果你这样做两次，你会注意到轴看起来很粗，图形很难看清。这是因为轴上的刻度设置为1。按[WINDOW]并向下滚动到Xscl。如果你按下[DELETE]，这将删除所有刻度。（你也可以将刻度设置为更大的值。）为了更好地查看图形，你还可以减小Xmin和Xmax。将Xmin设置为−20，将Xmax设置为20。按[GRAPH]。现在你可以看到函数了。按[TRACE]向任一方向移动，你将能够看到图形的左侧继续向下，右侧继续向上。

c. x截距：要将图形返回到较小的窗口，请按[ZOOM] [6]。如果你想在较小的窗口中查看图形，请按[ZOOM] [4]。你应该看到图形有3个x截距。你可以通过跟踪直观地近似它们：按[TRACE]并将光标向左移动。最左边的x截距大约为−0.5。要找到x截距的良好近似值，请按[2nd] [TRACE] [2]。这会将你送回图形。在屏幕上，你将看到问题“左边界？”将光标移动到x截距的左侧。（在这种情况下，你将向下移动。）按[ENTER]。然后你将看到问题“右边界？”将光标移动到x截距的右侧，但不要移动太远（不要超过下一个x截距。）按[ENTER]。然后将要求你“猜测”截距。将光标移回左侧，尽可能靠近x截距。按[ENTER]。你应该看到x = −0.5320888。这是x截距的近似值。如果你使用相同的步骤，你会发现其他x截距大约为0.6527和2.879。

d. 最大值和最小值：请注意，图形有一个“山峰”和一个“谷底”。山峰称为“局部最大值”，因为它是在某个区间内图形上的最高点。谷底类似地称为“局部最小值”。要近似最大值的坐标，请按[TRACE]并跟踪靠近最大值的位置。看起来最大值是 (0, 1)。要验证这一点，请按[2nd] [TRACE] [4]。要找到最大值，我们必须执行与查找x截距时相同的“左边界、右边界、猜测”过程。此过程应告诉你最大值为 (0, 1)。（注意：x值可能显示类似“9.64487E −7”的内容。这只是一个小的计算器误差。此数字非常接近0！）要找到最小值，请跟踪“谷底”。（如果需要，你可以转到[WINDOW]并将Ymin设置为更小的数字，以便你可以清楚地看到图形的最小值。）现在按[2nd] [TRACE] [3]。这会将你送回图形。执行“左边界、右边界、猜测”过程应显示最小点为 (2, −3)。

例6

你有100英尺长的栅栏，用来在谷仓旁边围一块地。你希望围成的地是矩形。

a. 写出一个函数来模拟地块面积与地块宽度的关系。

b. 使用绘图计算器绘制该函数的图像。

c. 你应该用栅栏围成什么尺寸的矩形才能使矩形围栏的面积最大化？

d. 解释x截距的意义。

解答:

地块将如下图所示

a. 方程：矩形地块的面积是其长和宽的乘积。我们可以将面积写成x的函数：A(x) = 2xh。如果我们考虑到我们有100英尺长的栅栏，并写出一个关于我们如何使用这100英尺栅栏的方程，我们就可以从方程中消去h：x + 2h = 100。（由于谷仓的存在，矩形的第四边不需要栅栏。）我们可以解出此方程以求得h，并将其代入面积方程

$x+2h=\,\!$	$100\Rightarrow 2h=100-x\Rightarrow h=50-{\frac {x}{2}}$
$A(x)=\,\!$	$2xh=2x\left(50-{\frac {x}{2}}\right)$
$A(x)=\,\!$	$100x-x^{2}\,\!$

b. 图形：按[Y=]并清除任何方程。然后在Y1中输入方程。请注意，如果你按下[ZOOM] [6]，你将看不到任何图形。你可以通过按下[ZOOM] [3]来缩小，但根据函数值选择窗口可能更有效。按[2nd] [WINDOW]

为了设置表格。TblStart 是您希望在表格中看到的第一个条目。Tbl 允许您设置增量。例如，如果您想看到x = 1、2、3、4 等，则将其设置为 1。对于此示例，将其设置为 10。确保 Indpnt 和 Depend（x 和 y）设置为“自动”。然后按[2nd] [GRAPH]查看表格。如果滚动浏览表格，您会发现当x = 50 时，y 值达到 2500，然后值开始下降。现在我们可以设置窗口。按[WINDOW]。并将 Xmin 设置为 -1，Xmax 设置为 105，Ymin 设置为 -200，Ymax 设置为 3000。（注意：您可以将 Xmin 和 Ymin 分别设置为 0，但将它们设置为 -1 和 -200 可以让您看到坐标轴。）

A(x) 的图形在此处显示在区间 [0, 100] 上。

c. 最大可能面积：使用示例 6 中的方法，您应该会发现 (50, 2500) 是最大点。这告诉我们，当矩形的宽度为 50 英尺时，面积为 2500 平方英尺。

d. 截距：使用示例 5 中的方法，您应该会发现x 截距位于 0 和 100。这告诉我们，如果花园的宽度为 0，则面积为 0。如果土地的宽度为 100，则面积为 0。这是因为只有 100 英尺的栅栏。如果宽度为 100，则矩形的其余部分没有更多的栅栏了！

三角函数简介

再次考虑上面提到的温度数据

如上所述，这种数据需要用周期函数来建模。特别是，这种数据通常由正弦曲线建模，正弦曲线以特定的方式振荡，如下面的图形所示。

每个正弦曲线都以规则的间隔重复其值。如果我们用这样的图形对天气数据进行建模，则值将每 12 个月重复一次。因此，我们说该函数的周期为 12。

请注意，数据范围约为 22 到 65。还要注意，“波浪”在这些值之间居中，大约在y = 43 处。因此，我们说波浪的振幅约为 21，即从中间到波浪顶部或底部的距离。

许多现实现象可以用这种函数来建模。

课程总结

在本课中，我们回顾了函数的概念，包括函数的主要方面和不同类型的函数。我们还使用了图形计算器来绘制和探索不同的函数。本课的一个关键点是我们可以使用函数来模拟现实现象。第二个关键点是，为了模拟本质上是循环的现象，我们需要使用周期函数。在本章的第 4 课中，我们将定义六个三角函数。但是，由于这些函数的输入是角度，所以在接下来的两节课中，我们将重点关注角度。首先，我们将回顾几何中的三角形角度，然后我们将考虑旋转中的角度。

思考点

是什么将函数与关系区分开来？
是什么使函数具有周期性？
使用计算器绘制函数图的优缺点是什么？

复习题

确定每个关系是否为函数
(a) (−1, 4), (0, 3)(1, 5), (1, 7), (2, 15)

(b) y = 3 - x

(c)
一列火车以每小时 95 英里的恒定速度行驶。
(a) 写出一个方程，表示火车行驶时间与行驶距离之间的关系。

(b) 这种情况是正比例关系、反比例关系还是都不是？

(c) 使用该方程确定火车在 3 小时后行驶的距离。
您决定开始一个小型企业，制作相框。您花费 100 美元购买油漆和其他用品，以及每个木制相框 2.00 美元。您决定以每个 10.00 美元的价格出售每个相框。
(a) 写出一个线性函数来模拟您业务的成本。

(b) 写出一个线性函数来模拟您业务的收入。（收入是您收到的金额。）

(c) 写出一个线性函数来模拟您业务的利润。（利润可以通过从收入中减去成本来找到。）

(d) 使用您的利润函数确定必须销售的最低相框数量才能获利。
考虑由方程f(x) = x² − x − 3 定义的函数。
(a) 此函数属于哪个函数族？

(b) 说明该函数的定义域和值域。

(c) 使用图形计算器绘制函数图，以识别顶点的近似坐标和x 截距的近似值。
考虑函数 $y={\tfrac {x-2}{x+3}}$
(a) 使用图形计算器绘制函数图。

(b) 识别所有渐近线。
在一间餐厅预订一个私人派对房间的价格为 500 美元。每人的价格与参加派对的人数成反比。
(a) 写出一个方程，表示每人成本 c 与参加人数 p 之间的关系。

(b) 如果有 32 人参加，使用该方程求出每人的成本。
使用图形计算器绘制函数y = x³ + x、y = x³ + 2x、y = x³ − x 和y = x³ − 2x 的图。改变第二项系数会产生什么影响？
方程p(x) = −.5x² + 90x − 200 表示一家公司的利润，其中 x 是该公司销售的单位数量。使用图形计算器绘制函数图，并使用图形回答问题。
(a) 最大利润是多少，必须销售多少单位才能达到最大利润？

(b) 找到x 截距，并解释这些点在图形上的含义，即公司的利润。
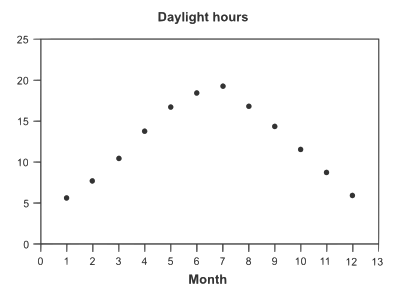
下表显示了阿拉斯加安克雷奇每个月的平均日照时间。
(a) 使用图形计算器绘制数据图，或手工绘制图。使用 1 月 = 1。

(b) 数据的周期是多少？

(c) 如果数据表示您居住地的日照时间，图形可能会有何不同？

表 1.5
月份	平均日照时间
一月	5.65
二月	7.77
三月	10.4
四月	13.37
五月	16.87
六月	18.72
七月	19.18
八月	17.12
九月	14.27
十月	11.43
十一月	8.53
十二月	6.13

复习答案

(a) 不是函数

(b) 是函数

(c) 不是函数
(a) y = 95x

(b) 这种情况是正比例关系。

(c) 285 英里
(a) C(x) = 2x + 100

(b) R(x) = 10x

(c) P(x) = 8x - 100

(d) 您必须制作和销售 13 个相框才能获利。
(a) 这是一个二次函数。

(b) 定义域是所有实数的集合。值域是大于或等于 3.25 的所有实数的集合。

(c) 顶点：(0.5, -3.25)；x 截距：-1.3、2.3
(a)

(b) x = -3, y = 1
(a) $cp=500\quad {\text{or}}\quad c={\frac {500}{p}}\quad {\text{or}}\quad p={\frac {500}{c}}$

(b) 15.63 美元
当系数增大时，具有正系数的方程越来越像y = x³。具有负系数的方程具有局部最大值和最小值。减小系数会增加“山峰”和“山谷”的大小。
(a) 最大利润为 3,850 美元，销售 90 个单位。

(b) 2.25 和 177.75。这些是盈亏平衡点。当销售 2-3 个单位时，公司已赚取足够的钱来弥补初始成本。在销售 177 个单位后，公司不再盈利。
(a)

(b) 周期 = 12

(c) 在美国其他城市，日照时间变化不大。图形的振幅会更小。

词汇表

因变量: 函数的自变量，通常用x表示。
定义域: 定义域是函数定义的自变量 (x) 的集合。
函数: 一种关系，其中定义域的每个元素都与值域的恰好一个元素配对。
自变量: 函数的输出变量，通常用y表示。
周期函数: 任何规律重复的函数。
值域: 函数的输出值或函数值 (y) 的集合。
关系: 两组数字或数据中的项目之间的配对。; 坐标是图或函数中的两个点；

← 三角学与直角 · 三角形中的角 →

此材料改编自可在此处找到的原始 CK-12 图书。此作品根据知识共享署名-相同方式共享 3.0 美国许可证授权。