高中三角函数/任意角的三角函数

在上一课中，我们介绍了六个三角函数，并且以两种方式处理这些函数：首先，在直角三角形中，其次，对于旋转角度。在本课中，我们将扩展对单位圆中任意角度的三角函数的工作，包括负角度和大于 360 度的角度。在上一课中，我们处理了象限角和 30°、45° 和 60° 角。在本课中，我们将处理与这些角度相关的角度，以及单位圆中的其他角度。本课的一个关键思想是角度可以共享相同的三角值。这个想法将在整节课中进行阐述。

学习目标

识别单位圆中角度的参考角。
识别参考角为 30°、45° 和 60° 或象限角（包括负角度和度数大于 360° 的角度）的角度在单位圆上的有序对。
使用这些有序对确定这些角度的三角函数值。
使用表格和计算器查找任意角度的三角函数值。

参考角和单位圆中的角度

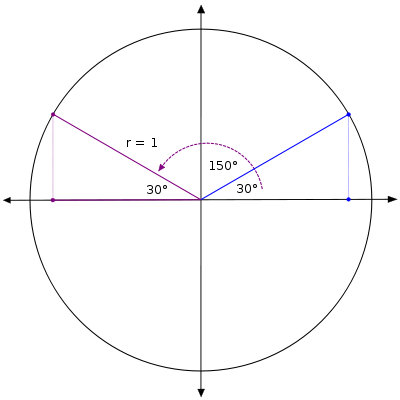
在上一课中，一个复习问题要求你考虑 150° 角。如果我们在标准位置绘制这个角，我们会看到这个角的终边是 30° 的终边关于y轴的对称。

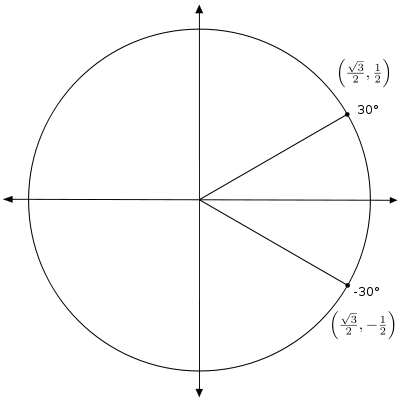
注意 150° 与负x轴形成一个 30° 角。因此，我们说 30° 是 150° 的参考角。正式地说，标准位置角度的参考角是与x轴最近部分形成的角度。请注意，30° 是许多角度的参考角。例如，它是 210° 和 −30° 的参考角。

一般来说，确定角度的参考角将有助于你确定角度的三角函数值。

示例 1

绘制每个角度并确定其参考角。

a. 140°

b. 240°

c. 380°

解决方案:

a. 140° 与x轴形成 40° 角。因此，参考角为 40°。

b. 240° 与x轴形成 60° 角。因此，参考角为 60°。

c. 380° 是 360° 的完整旋转，加上另外 20°。所以这个角与 20° 同向，而 20° 是它的参考角。

如果一个角度的参考角为 30°、45° 或 60°，我们可以确定它在单位圆上的有序对，因此我们可以找到该角度的六个三角函数的值。例如，上面我们指出 150° 的参考角为 30°。由于它与 30° 的关系，150° 的有序对是 $\left(-{\tfrac {\sqrt {3}}{2}},{\tfrac {1}{2}}\right)$ 。现在我们可以找到 150° 的六个三角函数的值

$\cos(150^{\circ })=x={\frac {-{\sqrt {3}}}{2}}$	$\sec(150^{\circ })={\frac {1}{x}}={\frac {1}{\frac {-{\sqrt {3}}}{2}}}={\frac {-2}{\sqrt {3}}}$
$\sin(150^{\circ })=y={\frac {1}{2}}$	$\csc(150^{\circ })={\frac {1}{y}}={\frac {1}{\frac {1}{2}}}=2$
$\tan(150^{\circ })={\frac {y}{x}}={\frac {\frac {1}{2}}{\frac {-{\sqrt {3}}}{2}}}={\frac {1}{-{\sqrt {3}}}}$	$\cot(150^{\circ })={\frac {x}{y}}={\frac {\frac {-{\sqrt {3}}}{2}}{\frac {1}{2}}}=-{\sqrt {3}}$

示例 2

找到 240° 的有序对，并用它来找到 sin 240° 的值。

解决方案:

sin(240°) = ${\tfrac {-{\sqrt {3}}}{2}}$

正如我们在示例 1 中发现的，240° 的参考角是 60°。下图显示了 60° 以及单位圆中其他三个以 60° 为参考角的角。

240° 的终边是 60° 的终边关于两个轴的反射。所以该点的坐标是 $\left(-{\tfrac {1}{2}},-{\tfrac {\sqrt {3}}{2}}\right)$ 。y 坐标是正弦值，所以 sin(240°) = ${\tfrac {-{\sqrt {3}}}{2}}$ 。

就像上图显示了 60° 和三个相关的角一样，我们也可以为 30° 和 45° 制作类似的图形。

示例 3

求 cot(300°) 的值。

解决方案:

cot(300°) = $-{\tfrac {1}{\sqrt {3}}}$

使用上面的图形，你会发现该点的坐标是 $\left({\tfrac {1}{2}},-{\tfrac {\sqrt {3}}{2}}\right)$ 。因此余切值为

$\cot(300^{\circ })={\frac {x}{y}}={\frac {\frac {1}{2}}{-{\frac {\sqrt {3}}{2}}}}={\frac {1}{2}}\cdot -{\frac {2}{\sqrt {3}}}=-{\frac {1}{\sqrt {3}}}$

我们还可以使用参考角的概念和我们已经确定的坐标对来确定其他角的三角函数的值。

负角的三角函数

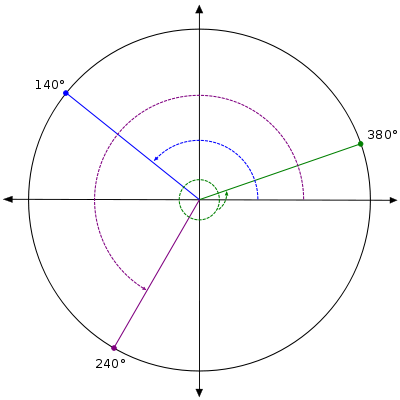
回想一下，绘制负角意味着顺时针旋转。下图显示了 -30°。

注意，这个角与 330° 是终边相同的。因此该点的坐标是 $\left({\tfrac {\sqrt {3}}{2}},-{\tfrac {1}{2}}\right)$ 。我们可以使用这个坐标对来求出 -30° 的任何三角函数的值。例如，cos(-30°) = x = ${\tfrac {\sqrt {3}}{2}}$ 。

一般来说，如果一个负角的参考角是 30°、45° 或 60°，或者它是一个象限角，我们可以找到它的坐标对，因此我们可以确定该角的任何三角函数的值。

示例 4

求每个表达式的值。

a. sin(-45°)

b. sec(-300°)

c. cos(-90°)

解决方案:

a. sin(-45°) = $-{\tfrac {\sqrt {2}}{2}}$

−45° 位于第四象限，其参考角为 45°。也就是说，该角度与 315° 终边重合。因此，有序对是 $\left({\tfrac {\sqrt {2}}{2}},-{\tfrac {\sqrt {2}}{2}}\right)$ ，正弦值为 $-{\tfrac {\sqrt {2}}{2}}$ 。

b. sec(-300°) = 2

角度 −300° 位于第一象限，其参考角为 60°。也就是说，该角度与 60° 终边重合。因此，有序对是 $\left({\tfrac {1}{2}},{\tfrac {\sqrt {3}}{2}}\right)$ ，正割值为 ${\tfrac {1}{x}}={\tfrac {1}{\frac {1}{2}}}=$ 2。

c. cos(−90°) = 0

角度 −90° 与 270° 终边重合。因此，有序对为 (0, −1)，余弦值为 0。

我们还可以利用对参考角和有序对的了解，找到大于 360 度的角度的三角函数值。

大于 360 度的角度的三角函数

考虑角度 390°。正如你之前所学，你可以将这个角度视为一个完整的 360 度旋转，再加上额外的 30 度。因此，390° 与 30° 终边重合。正如你在上面关于负角度的讨论中看到的那样，这意味着 390° 与 30° 具有相同的有序对，因此它们具有相同的三角函数值。例如，cos(390°) = cos(30°) = ${\tfrac {\sqrt {3}}{2}}K$

一般来说，如果一个大于 360 度的角度的参考角为 30°、45° 或 60°，或者它是一个象限角，我们可以找到它的有序对，因此我们可以找到该角度的任何三角函数的值。第一步是确定参考角。

例 5

求每个表达式的值。

a. sin(420°)

b. tan(840°)

c. cos(540°)

解决方案:

a. sin(420°) = ${\tfrac {\sqrt {3}}{2}}$

420° 是一个完整的 360 度旋转，再加上额外的 60 度。因此，该角度与 60° 终边重合，因此它具有相同的有序对， $\left({\tfrac {1}{2}},{\tfrac {\sqrt {3}}{2}}\right)$ 。正弦值是 *y* 坐标。

b. tan(840°) = −√3

840° 是两个完整的旋转，或 720 度，再加上额外的 120 度

840 = 360 + 360 + 120

因此，840° 与 120° 终边重合，所以有序对是 $\left(-{\tfrac {1}{2}},{\tfrac {\sqrt {3}}{2}}\right)$ 。正切值可以通过以下方法找到

\tan(840^{\circ })=\tan(120^{\circ })={\frac {y}{x}}={\frac {\frac {\sqrt {3}}{2}}{-{\frac {1}{2}}}}={\frac {\sqrt {3}}{2}}\cdot -{\frac {2}{1}}=-{\sqrt {3}}

c. cos(540°) = −1

540° 是一个完整的 360 度旋转，再加上额外的 180 度。因此，该角度与 180◦ 终边重合，有序对为 (−1, 0)。所以余弦值为 −1。

到目前为止，我们处理的所有角度都是 30、45、60 和 90 的倍数。接下来，我们将找到其他角度的三角函数的近似值。

三角函数值表

在学习这章的过程中，你将学习到三角函数的不同应用。在许多情况下，你将需要找到一个角度的函数值，该角度不一定是我们迄今为止处理过的“特殊”角度之一。传统上，教科书会为学生提供包含三角函数值的表格。下面是一个表格，它提供了几个角度的正弦、余弦和正切值的近似值。

表 1.11
角度 (°)	余弦	正弦	正切
0	1.000	0.000	0.000
5	0.9962	0.0872	0.0875
10	0.9848	0.1736	0.1763
15	0.9659	0.2588	0.2679
20	0.9397	0.3420	0.3640
25	0.9063	0.4226	0.4663
30	0.8660	0.5000	0.5774
35	0.8192	0.5736	0.7002
40	0.7660	0.6428	0.8391
45	0.7071	0.7071	1.0000
50	0.6428	0.7660	1.1918
55	0.5736	0.8192	1.4281
60	0.5000	0.8660	1.7321
65	0.4226	0.9063	2.1445
70	0.3420	0.9397	2.7475
75	0.2588	0.9659	3.7321
80	0.1736	0.9848	5.6713
85	0.0872	0.9962	11.4301
90	0.0000	1.0000	未定义
95	−0.0872	0.9962	−11.4301
100	−0.1736	0.9848	−5.6713
105	−0.2588	0.9659	−3.7321
110	−0.3420	0.9397	−2.7475
115	−0.4226	0.9063	−2.1445
120	−0.5000	0.8660	−1.7321
125	−0.5736	0.8192	−1.4281
130	−0.6428	0.7660	−1.1918
135	−0.7071	0.7071	−1.0000
140	−0.7660	0.6428	−0.8391
145	−0.8192	0.5736	−0.7002
150	−0.8660	0.5000	−0.5774
155	−0.9063	0.4226	−0.4663
160	−0.9397	0.3420	−0.3640
165	−0.9659	0.2588	−0.2679
170	−0.9848	0.1736	−0.1763
175	−0.9962	0.0872	−0.0875
180	−1.0000	0.0000	0.0000

我们可以用表格来识别近似值。

例 6

使用上面的表格，找到每个表达式的近似值。

a. sin(130°)

b. cos(15°)

c. tan(50°)

解决方案:

a. sin(130°) ≈ 0.7660

我们可以通过查找表格中 130 度的行来确定正弦值。正弦值位于表格的第三行。请注意，这是一个近似值。我们可以通过考虑一个接近 130 度的角，120 度，来评估此值的合理性。我们知道 120 度的有序对是 $\left(-{\tfrac {1}{2}},{\tfrac {\sqrt {3}}{2}}\right)$ ，因此正弦值为 ${\tfrac {\sqrt {3}}{2}}$ ≈ 0.8660，这也位于表格中。由于这些角的终边与单位圆的交点，sin(130°) ≈ 0.7660 是合理的，它略小于 120 度的正弦值。

b. cos(15°) ≈ 0.9659

我们可以通过查找 15 度的行来确定此余弦值。余弦值位于第二列。同样，我们可以通过考虑一个附近的角来确定此值是否合理。15° 在 0° 和 30° 之间，其余弦值在这两个角的余弦值之间。

c. tan(50°) ≈ 1.1918

我们可以通过查找 50 度的行，并读取表格的最后一列来确定此正切值。在复习题中，您将被要求解释为什么正切值似乎是合理的。

使用计算器查找值

如果您有科学计算器，您可以确定任何角的任何三角函数的值。在这里，我们将重点介绍使用 TI 图形计算器查找值。

首先，您的计算器需要处于正确的“模式”。在第 2 章中，您将学习另一种测量角度的系统，称为弧度制。在本章中，我们以度为单位测量角度。（这类似于以英里或公里为单位测量距离。它只是不同的测量系统。）我们需要确保计算器以度为单位工作。为此，请按[MODE]. 您将看到第三行显示 Radian Degree。如果 Degree 被突出显示，则您处于正确的模式。如果 Radian 被突出显示，请向下滚动到此行，向右滚动到 Degree，然后按[ENTER]. 这将突出显示 Degree。然后按 2^nd[MODE]返回主屏幕。

现在您可以计算任何值。例如，我们可以验证上述表格中的值。要查找 sin(130°)，请按[SIN] [1] [3] [0] [ENTER]. 计算器应返回值 .7660444431。

您可能已经注意到，计算器在 SIN 后提供了 "("。在前面的计算中，您实际上可以省略 ")"。但是，在更复杂的计算中，省略右括号")" 会导致问题。养成习惯，始终闭合括号是个好主意。

您也可以使用计算器查找更复杂表达式的值。

例 7

使用计算器查找 sin(25°) + cos(25°) 的近似值。将您的答案四舍五入到小数点后 4 位。

解决方案:

sin(25°) + cos(25°) ≈ 1.3289

要使用 TI 图形计算器，请按[SIN] [25] [+] [COS] [2] [5] [ENTER]. 计算器应返回数字 1.328926049。四舍五入到 1.3289。

课程总结

在本课中，我们已经研究了我们可以为任何角度找到六个三角函数的精确值或近似值的概念。我们首先定义了参考角的概念，这对于找到单位圆中某些角度的有序对很有用。我们已经找到了“特殊”角度的三角函数的精确值，包括负角以及度数大于 360 度的角。我们还使用表格和计算器找到了其他角度值的近似值。在接下来的课程中，我们将使用本课中的概念来 (1) 检查三角函数之间的关系，以及 (2) 将三角函数应用于实际情况。

值得思考的问题

角度的度数与其参考角之间有什么区别？在哪些情况下这些度数相同？
哪些角具有相同的余弦值或相同的正弦值？哪些角具有相反的余弦值和正弦值？

复习题

说明每个角的参考角。
(a) 190°

(b) −60°

(c) 1470°

(d) −135°
说明每个角的有序对。
(a) 300°

(b) −150°

(c) 405°
求每个表达式的值。
(a) sin(210°)

(b) tan(270°)

(c) csc(120°)
求每个表达式的值。
(a) sin(510°)

(b) cos(930°)

(c) csc(405°)
求每个表达式的值。
(a) cos(−150°)

(b) tan(−45°)

(c) sin(−240°)
使用本课中的表格查找 cos(100°) 的近似值。
使用本课中的表格来近似一个正弦值为 0.2 的角度的度数。
在例 6c 中，我们发现 tan(50°) ≈ 1.1918。使用您对特殊角的了解来解释为什么此值是合理的。
使用计算器查找每个值。四舍五入到小数点后 4 位。
(a) sin(118°)

(b) tan(55°)
使用下面的表格或计算器来探索三角函数之间的和与积关系。
考虑以下函数
f(x) = sin(x+x) 和 g(x) = sin(x) + sin(x)

h(x) = sin(x) · sin(x) 和 j(x) = sin(x²)

您是否在这些函数中观察到任何规律？函数之间是否存在任何等式？您能对所有 a、b 值的 sin(a) + sin(b) 和 sin(a+b) 作出一般性推测吗？

sin(a) · sin(a) 和 sin(a²) 又如何呢？

a° b° sin a + sin b sin(a+b)
10 30 0.6736 0.6428
20 60 1.2080 0.9848
55 78 1.7973 0.7314
122 25 1.2707 0.5446
200 75 0.6239 −0.9962
使用计算器或您对特殊角的了解来填写表格中的值，然后使用这些值来推测 (sin a)² 和 (cos a)² 之间的关系。如果您使用计算器，请将所有值四舍五入到小数点后 4 位。
a (sin a)² (cos a)²
0
25
45
80
90
120
250

复习答案

(a) 10°

(b) 60°

(c) 30°

(d) 45°
(a) $\left({\tfrac {1}{2}},-{\tfrac {\sqrt {3}}{2}}\right)$

(b) $\left(-{\tfrac {\sqrt {3}}{2}},-{\tfrac {1}{2}}\right)$

(c) $\left({\tfrac {\sqrt {2}}{2}},{\tfrac {\sqrt {2}}{2}}\right)$
(a) $-{\tfrac {1}{2}}$

(b) 未定义

(c) ${\tfrac {2}{\sqrt {3}}}$
(a) ${\tfrac {1}{2}}$

(b) $-{\tfrac {\sqrt {3}}{2}}$

(c) √2
(a) $-{\tfrac {\sqrt {3}}{2}}$

(b) −1

(c) ${\tfrac {\sqrt {3}}{2}}$
−0.1736
介于 165 度和 160 度之间。
这是合理的，因为 tan(45°) = 1 。
(a) 0.8828

(b) 1.4281
猜想：sin a + sin b ≠ sin(a+b) 。
猜想：(sin a)² + (cos a)² = 1 。
a (sin a)² (cos a)²
0 0 1
25 0.1786 0.8216
45 0.5000 0.5000
80 0.9698 0.0302
90 1 0
120 0.7500 0.2500
250 0.8830 0.1170