线性代数/行列式作为大小函数

线性代数
← 行列式的几何意义	行列式作为大小函数	行列式的其他公式 →

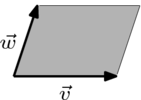
这个平行四边形图

是我们从两个向量的和的构造中熟悉的。计算它所包围的面积的一种方法是画出这个矩形，然后减去每个子区域的面积。

${\begin{array}{l}{\text{area of parallelogram}}\\\quad ={\text{area of rectangle}}-{\text{area of }}A-{\text{area of }}B\\\qquad -\cdots -{\text{area of }}F\\\quad =(x_{1}+x_{2})(y_{1}+y_{2})-x_{2}y_{1}-x_{1}y_{1}/2\\\qquad -x_{2}y_{2}/2-x_{2}y_{2}/2-x_{1}y_{1}/2-x_{2}y_{1}\\\quad =x_{1}y_{2}-x_{2}y_{1}\end{array}}$

面积等于行列式的值

{\begin{vmatrix}x_{1}&x_{2}\\y_{1}&y_{2}\end{vmatrix}}=x_{1}y_{2}-x_{2}y_{1}

并非巧合。行列式定义中的性质为衡量矩阵中向量所包围区域大小的函数提供了合理的假设。

例如，这显示了将一个定义方框的向量乘以一个标量（使用的标量为 $k=1.4$ ）。

由 $k{\vec {v}}$ 和 ${\vec {w}}$ 所形成的区域比由 ${\vec {v}}$ 和 ${\vec {w}}$ 所围成的阴影区域大 $k$ 倍。也就是说， ${\text{size}}\,(k{\vec {v}},{\vec {w}})=k\cdot {\text{size}}\,({\vec {v}},{\vec {w}})$ ，一般来说，我们期望大小度量具有 ${\text{size}}\,(\dots ,k{\vec {v}},\dots )=k\cdot {\text{size}}\,(\dots ,{\vec {v}},\dots )$ 的性质。当然，这个假设已经是我们熟知的行列式定义中的性质之一。

行列式的另一个性质是它们不受旋转的影响。以下是旋转前后的盒子（使用的标量是 $k=0.35$ ）。

虽然右边的区域，由 $v$ 和 $k{\vec {v}}+{\vec {w}}$ 所形成的盒子，比阴影区域更倾斜，但它们具有相同的底边和高度，因此面积也相同。这说明了 ${\text{size}}\,({\vec {v}},k{\vec {v}}+{\vec {w}})={\text{size}}\,({\vec {v}},{\vec {w}})$ 。推广来说， ${\text{size}}\,(\dots ,{\vec {v}},\dots ,{\vec {w}},\dots )={\text{size}}\,(\dots ,{\vec {v}},\dots ,k{\vec {v}}+{\vec {w}},\dots )$ ，这是行列式假设的另一种说法。

当然，这张图片

表明 ${\text{size}}\,({\vec {e}}_{1},{\vec {e}}_{2})=1$ ，我们自然地将其扩展到任意维数 ${\text{size}}\,({\vec {e}}_{1},\dots ,{\vec {e}}_{n})=1$ ，这是单位矩阵行列式为 1 的性质的另一种说法。

有了这一点，因为行列式的性质 (2) 是多余的（正如在定义之后立即提到的），所以我们得出，所有行列式的性质都是对一个给出盒子大小的函数的合理预期。现在，我们可以引用上一节中所做的工作来证明行列式的存在性和唯一性，以确保这些假设是一致且充分的（我们不需要任何更多的假设）。也就是说，我们得到了一个直观的理由来解释 $\det({\vec {v}}_{1},\dots ,{\vec {v}}_{n})$ 作为由这些向量形成的盒子的大小。（注释。 一种更基本的方法，它也导致下面的定义，在 (Weston 1959) 中。）

例 1.1

这个平行六面体的体积可以通过高中几何中的通常公式求得，为 $12$ 。

${\begin{vmatrix}2&0&-1\\0&3&0\\2&1&1\end{vmatrix}}=12$

备注 1.2

虽然定义中的性质 (2) 是多余的，但它提出了一个重要的观点。考虑这两个。


${\begin{vmatrix}4&1\\2&3\end{vmatrix}}=10$	${\begin{vmatrix}1&4\\3&2\end{vmatrix}}=-10$

它们之间唯一的区别是向量被取的顺序。如果我们首先取 ${\vec {u}}$ ，然后转到 ${\vec {v}}$ ，沿着所示的逆时针弧线，那么符号为正。沿着顺时针弧线会得到负号。大小函数返回的符号反映了盒子的“方向”或“意义”。（如果我们想象一个负标量乘以一个标量的效果，我们会看到同样的事情。）

虽然方向的概念既有趣又重要，但它实际上很棘手。在下面的开发过程中不需要它，所以我们将跳过它。（见问题 20。）

定义 1.3

由 $\langle {\vec {v}}_{1},\dots ,{\vec {v}}_{n}\rangle$ (其中每个向量来自 $\mathbb {R} ^{n}$ ) 所形成的箱子（或平行六面体）包含集合 $\{t_{1}{\vec {v}}_{1}+\dots +t_{n}{\vec {v}}_{n}\,{\big |}\,t_{1},\ldots ,t_{n}\in [0..1]\}$ 的所有元素。箱子的体积是将这些向量作为列的矩阵的行列式的绝对值。

示例 1.4

体积，由于它是绝对值，因此不依赖于向量的给出顺序。示例 1.1 中的平行六面体的体积也可以计算为该行列式的绝对值。

{\begin{vmatrix}0&2&-1\\3&0&0\\1&2&1\end{vmatrix}}=-12

体积的定义为空间中的某事物提供了几何解释，即由向量构成的箱子。下一个结果将几何与作用于空间的函数联系起来。

定理 1.5

变换 $t:\mathbb {R} ^{n}\to \mathbb {R} ^{n}$ 以相同因子改变所有箱子的尺寸，即箱子 $\left|t(S)\right|$ 的图像的大小是 $\left|T\right|$ 倍的箱子 $\left|S\right|$ 的大小，其中 $T$ 是相对于标准基表示 $t$ 的矩阵。也就是说，对于所有 $n\!\times \!n$ 矩阵，乘积的行列式等于行列式的乘积 $\left|TS\right|=\left|T\right|\cdot \left|S\right|$ 。

这两句话表达了同一个意思，第一句话用映射的术语，第二句话用矩阵的术语。虽然我们倾向于使用映射的观点，但第二句话，矩阵的版本，在证明中更方便，也是我们以后使用该结果的方式。（备选证明见问题 16和问题 21）。

证明

这两个表达式是等价的，因为 $\left|t(S)\right|=\left|TS\right|$ ，它们都表示单位立方体 ${\mathcal {E}}_{n}$ 在复合变换 $t\circ s$ 下的像的体积（其中 $s$ 是由 $S$ 关于标准基表示的映射）。

现在考虑这种情况， $\left|T\right|\neq 0$ ，即 $T$ 是非奇异的。回想一下，任何非奇异矩阵都可以分解成初等矩阵的乘积，因此 $TS=E_{1}E_{2}\cdots E_{r}S$ 。在接下来的论证中，我们将验证如果 $E$ 是一个初等矩阵，则 $\left|ES\right|=\left|E\right|\cdot \left|S\right|$ 。结果将随之而来，因为然后 $\left|TS\right|=\left|E_{1}\cdots E_{r}S\right|=\left|E_{1}\right|\cdots \left|E_{r}\right|\cdot \left|S\right|=\left|E_{1}\cdots E_{r}\right|\cdot \left|S\right|=\left|T\right|\cdot \left|S\right|$ .

如果初等矩阵 $E$ 是 $M_{i}(k)$ ，那么 $M_{i}(k)S$ 等于 $S$ ，除了第 $i$ 行被乘以 $k$ 。那么行列式函数的第三个性质就表明 $\left|M_{i}(k)S\right|=k\cdot \left|S\right|$ 。但 $\left|M_{i}(k)\right|=k$ ，同样由第三个性质得出，因为 $M_{i}(k)$ 是通过将单位矩阵的第 $i$ 行乘以 $k$ 得到的，因此 $\left|ES\right|=\left|E\right|\cdot \left|S\right|$ 对 $E=M_{i}(k)$ 成立。 $E=P_{i,j}=-1$ 和 $E=C_{i,j}(k)$ 的检验类似。

示例 1.6

用标准基表示的映射 $t$ 的应用

{\begin{pmatrix}1&1\\-2&0\end{pmatrix}}

将使盒子的尺寸翻倍，例如从以下

${\begin{vmatrix}2&1\\1&2\end{vmatrix}}=3$

到以下

${\begin{vmatrix}3&3\\-4&-2\end{vmatrix}}=6$

推论 1.7

如果一个矩阵可逆，那么它的逆矩阵的行列式等于其行列式的倒数 $\left|T^{-1}\right|=1/\left|T\right|$ .

证明

$1=\left|I\right|=\left|TT^{-1}\right|=\left|T\right|\cdot \left|T^{-1}\right|$

回想一下，行列式不是加法同态， $\det(A+B)$ 不一定等于 $\det(A)+\det(B)$ 。相反，上述定理说明行列式是乘法同态： $\det(AB)$ 等于 $\det(A)\cdot \det(B)$ .

练习

问题 1

求形成的区域的体积。

$\langle {\begin{pmatrix}1\\3\end{pmatrix}},{\begin{pmatrix}-1\\4\end{pmatrix}}\rangle$
$\langle {\begin{pmatrix}2\\1\\0\end{pmatrix}},{\begin{pmatrix}3\\-2\\4\end{pmatrix}},{\begin{pmatrix}8\\-3\\8\end{pmatrix}}\rangle$
$\langle {\begin{pmatrix}1\\2\\0\\1\end{pmatrix}},{\begin{pmatrix}2\\2\\2\\2\end{pmatrix}},{\begin{pmatrix}-1\\3\\0\\5\end{pmatrix}},{\begin{pmatrix}0\\1\\0\\7\end{pmatrix}}\rangle$

建议所有读者做这道练习。

问题 2

是

{\begin{pmatrix}4\\1\\2\end{pmatrix}}

在由这三个向量形成的箱子里？

{\begin{pmatrix}3\\3\\1\end{pmatrix}}\quad {\begin{pmatrix}2\\6\\1\end{pmatrix}}\quad {\begin{pmatrix}1\\0\\5\end{pmatrix}}

建议所有读者做这道练习。

问题 3

求该区域的体积。

建议所有读者做这道练习。

问题 4

假设 $\left|A\right|=3$ 。这些变换改变体积的比例是多少？

$A$
$A^{2}$
$A^{-2}$

建议所有读者做这道练习。

问题 5

每个变换改变盒子大小的比例是多少？

${\begin{pmatrix}x\\y\end{pmatrix}}\mapsto {\begin{pmatrix}2x\\3y\end{pmatrix}}$
${\begin{pmatrix}x\\y\end{pmatrix}}\mapsto {\begin{pmatrix}3x-y\\-2x+y\end{pmatrix}}$
${\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto {\begin{pmatrix}x-y\\x+y+z\\y-2z\end{pmatrix}}$

问题 6

在该矩阵作用下，矩形 $[2..4]\times [2..5]$ 的图像的面积是多少？

{\begin{pmatrix}2&3\\4&-1\end{pmatrix}}

问题 7

如果 $t:\mathbb {R} ^{3}\to \mathbb {R} ^{3}$ 将体积改变了 $7$ 倍，而 $s:\mathbb {R} ^{3}\to \mathbb {R} ^{3}$ 将体积改变了 $3/2$ 倍，那么它们的复合变换将体积改变多少倍？

问题 8

盒子的定义与生成空间的定义有何区别？

建议所有读者做这道练习。

问题 9

为什么这张图没有与定理 1.5 矛盾？

	${\xrightarrow[{}]{\scriptstyle {\begin{pmatrix}2&1\\0&1\end{pmatrix}}}}$
面积为 $2$	行列式为 $2$	面积为 $5$

建议所有读者做这道练习。

问题 10

问题 11

假设 $\left|A\right|=3$ 且 $\left|B\right|=2$ 。求 $\left|A^{2}\cdot {{B}^{\rm {trans}}}\cdot B^{-2}\cdot {{A}^{\rm {trans}}}\right|$ 。
假设 $\left|A\right|=0$ 。证明 $\left|6A^{3}+5A^{2}+2A\right|=0$ 。

建议所有读者做这道练习。

问题 12

设 $T$ 是表示将平面向量逆时针旋转 $\theta$ 弧度的映射（相对于标准基）的矩阵。 $T$ 将大小改变了多少倍？

建议所有读者做这道练习。

问题 13

一个保持面积的变换 $t:\mathbb {R} ^{2}\to \mathbb {R} ^{2}$ 是否也必须保持长度？

建议所有读者做这道练习。

问题 14

在 $\mathbb {R} ^{3}$ 中，由线性相关集所包围的平行六面体的体积是多少？

建议所有读者做这道练习。

问题 15

在 $\mathbb {R} ^{3}$ 中，端点为 $(1,2,1)$ 、 $(3,-1,4)$ 和 $(2,2,2)$ 的三角形的面积是多少？（面积，而不是体积。该三角形定义了一个平面——该平面上的三角形的面积是多少？）

建议所有读者做这道练习。

问题 16

对定理 1.5 的另一种证明使用行列式函数的定义。

注意，构成 $S$ 的向量构成线性相关集当且仅当 $\left|S\right|=0$ ，并检查结果在这种情况下是否成立。
对于 $\left|S\right|\neq 0$ 的情况，为了证明对所有变换都成立 $\left|TS\right|/\left|S\right|=\left|T\right|$ ，考虑由 $T\mapsto \left|TS\right|/\left|S\right|$ 给出的函数 $d:{\mathcal {M}}_{n\!\times \!n}\to \mathbb {R}$ 。证明 $d$ 具有行列式的第一个性质。
证明 $d$ 具有行列式函数的其余三个性质。
由此得出结论， $\left|TS\right|=\left|T\right|\cdot \left|S\right|$ .

问题 17

给出一个非单位矩阵，该矩阵具有 ${{A}^{\rm {trans}}}=A^{-1}$ 的性质。证明如果 ${{A}^{\rm {trans}}}=A^{-1}$ ，那么 $\left|A\right|=\pm 1$ 。反之是否成立？

问题 18

行列式的代数性质表明，从单个行中分解一个标量将使行列式乘以该标量，这表明当 $H$ 是 $3\!\times \!3$ 时， $cH$ 的行列式是 $c^{3}$ 乘以 $H$ 的行列式。用几何方式解释，即使用定理 1.5。

建议所有读者做这道练习。

问题 19

如果存在一个非奇异矩阵 $P$ 使得 $H=P^{-1}GP$ （我们将在第五章研究这种关系），则称矩阵 $H$ 和 $G$ **相似**。证明相似矩阵具有相同的行列式。

问题 20

我们通常用标准基表示 $\mathbb {R} ^{2}$ 中的向量，因此第一象限中的向量具有两个正坐标。

${\rm {Rep}}_{{\mathcal {E}}_{2}}({\vec {v}})={\begin{pmatrix}+3\\+2\end{pmatrix}}$

沿原点逆时针方向移动，我们会循环遍历四个区域

\cdots \;\longrightarrow {\begin{pmatrix}+\\+\end{pmatrix}}\;\longrightarrow {\begin{pmatrix}-\\+\end{pmatrix}}\;\longrightarrow {\begin{pmatrix}-\\-\end{pmatrix}}\;\longrightarrow {\begin{pmatrix}+\\-\end{pmatrix}}\;\longrightarrow \cdots \,.

使用此基

$B=\langle {\begin{pmatrix}0\\1\end{pmatrix}},{\begin{pmatrix}-1\\0\end{pmatrix}}\rangle$

给出了相同的逆时针循环。我们说这两个基具有相同的 *方向*。

为什么它们给出相同的循环？
轴上单位向量的哪些其他配置给出相同的循环？
找到从这些（有序）基形成的矩阵的行列式。
还有哪些逆时针循环是可能的，以及它们相关的行列式是什么？
在 $\mathbb {R} ^{1}$ 中会发生什么？
在 $\mathbb {R} ^{3}$ 中会发生什么？

关于方向的引人入胜的普通观众讨论见 (Gardner 1990)。

问题 21

这个问题使用了可选的行列式函数存在子部分中的材料。使用行列式的排列展开公式证明定理 1.5。

建议所有读者做这道练习。

问题 22

证明这给出了 $\mathbb {R} ^{2}$ 中过 $(x_{2},y_{2})$ 和 $(x_{3},y_{3})$ 的直线的方程。
${\begin{vmatrix}x&x_{2}&x_{3}\\y&y_{2}&y_{3}\\1&1&1\end{vmatrix}}=0$
(Peterson 1955) 证明顶点为 $(x_{1},y_{1})$ ， $(x_{2},y_{2})$ 和 $(x_{3},y_{3})$ 的三角形的面积为
${\frac {1}{2}}{\begin{vmatrix}x_{1}&x_{2}&x_{3}\\y_{1}&y_{2}&y_{3}\\1&1&1\end{vmatrix}}.$
(Bittinger 1973) 证明顶点在 $(x_{1},y_{1})$ , $(x_{2},y_{2})$ , 和 $(x_{3},y_{3})$ 的坐标都是整数的三角形的面积为 $N$ 或 $N/2$ ，其中 $N$ 是一个正整数。

解决方案

参考资料

Bittinger, Marvin (proposer) (1973), "Quickie 578", Mathematics Magazine, 美国数学学会, 46 (5): 286, 296 {{citation}}: 未知参数 |month= 被忽略了 (帮助).
Gardner, Martin (1990), The New Ambidextrous Univers, W. H. Freeman and Company {{citation}}: 未知参数 |editition= 被忽略了 (帮助).
Peterson, G. M. (1955), "Area of a triangle", American Mathematical Monthly, 美国数学学会, 62 (4): 249 {{citation}}: 未知参数 |month= 被忽略了 (帮助).
Weston, J. D. (1959), "Volume in Vector Spaces", American Mathematical Monthly, 美国数学学会, 66 (7): 575–577 {{citation}}: 未知参数 |month= 被忽略了 (帮助).

线性代数
← 行列式的几何意义	行列式作为大小函数	行列式的其他公式 →