线性代数/命题

论证中的争议点是命题。数学家通常会在证明之前写出完整的论点，并将其标记为定理（对于主要论点）、推论（对于紧接在先前论点之后的论点）或引理（对于主要用于证明其他结果的结果）。

表达命题的陈述可能很复杂，包含许多子部分。整个命题的真假既取决于各部分的真值，也取决于用来将各部分组合成陈述的词语。

非

例如，当 $P$ 是一个命题时，"并非 $P$" 是真的，前提是 $P$ 是假的。因此，"$n$ 不是素数" 只有在 $n$ 是较小整数的乘积时才为真。

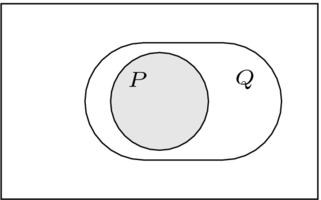
我们可以用文氏图来描述"非"操作。

框包含所有自然数，圆圈内是素数，阴影区域包含满足"非 $P$" 的数字。

要证明"非 $P$" 语句成立，请证明 $P$ 是假的。

与

考虑语句形式"$P$ 与 $Q$"。为了使该语句为真，两半都必须成立：" $7$ 是素数，$3$ 也是" 是真的，而 "$7$ 是素数，$3$ 不是" 是假的。

这是"$P$ 与 $Q$" 的文氏图。

要证明"$P$ 与 $Q$"，请证明每一半都成立。

或

当其中一个部分成立时，"$P$ 或 $Q$" 为真："$7$ 是素数，或 $4$ 是素数" 为真，而 "$7$ 不是素数，或 $4$ 是素数" 为假。我们对“或”采取包含性，因此，如果两个部分都为真，"$7$ 是素数，或 $4$ 不是"，那么整个语句就为真。（在日常语言中，有时“或”的意思是排他的——“吃蔬菜或没有甜点”并不意味着两个部分都成立——但我们不会用“或”来表达这种意思。）

“或”的维恩图包含两个圆的所有部分。

为了证明"$P$ 或 $Q$"，请证明在所有情况下，至少有一个部分成立（有时可能是其中一个部分，有时是另一个部分，但始终至少有一个成立）。

如果-那么

“如果 $P$ 那么 $Q$” 语句（有时写成“$P$ 蕴含 $Q$” 或简称为“$P$ 蕴含 $Q$” 或“$P\implies Q$”) 除非 $P$ 为真而 $Q$ 为假，为真。因此“如果 $7$ 是素数，那么 $4$ 不是”为真，而“如果 $7$ 是素数，那么 $4$ 也是素数”为假。（与日常用语中“如果 $P$ 那么 $Q$” 的含义不同，在数学中“如果 $P$ 那么 $Q$” 不意味着 $P$ 发生在 $Q$ 之前或导致 $Q$。）

更微妙的是，在数学中，“如果 $P$ 那么 $Q$” 当 $P$ 为假时成立：“如果 $4$ 是素数，那么 $7$ 是素数” 和 “如果 $4$ 是素数，那么 $7$ 不是” 都是真命题，有时被称为 **空真**。我们采用这种约定，因为我们希望像“如果一个数是完全平方，那么它就不是素数” 这样的命题为真，例如，当这个数为 $5$ 或当这个数为 $6$ 时。

这个图表

表明 $Q$ 只要 $P$ 成立就成立（另一种说法是“$P$ 足以得到 $Q$”)。再次注意，如果 $P$ 不成立，$Q$ 可能成立也可能不成立。

建立蕴涵关系主要有两种方式。第一种是直接方式：假设 $P$ 为真，并利用该假设证明 $Q$ 为真。例如，为了证明“如果一个数能被 5 整除，那么该数的两倍就能被 10 整除”，我们假设该数为 $5n$，并推导出 $2(5n)=10n$。 第二种是间接方式：证明逆否命题：“如果 $Q$ 为假，那么 $P$ 也为假”（换句话说，“$Q$ 只有在 $P$ 也为假时才可能为假”。例如，为了证明“如果一个数是素数，那么它就不是一个完全平方数”，我们论证如果它是一个平方数 $p=n^{2}$，那么它就可以分解成 $p=n\cdot n$，其中 $n<p$，因此就不是素数（当然 $p=0$ 或 $p=1$ 无法得到 $n<p$，但根据定义它们是非素数)。

请注意这种命题形式的两个特点。

首先，一个“如果 $P$ 那么 $Q$” 的结果有时可以通过削弱 $P$ 或加强 $Q$ 来改进。因此，“如果一个数字可以被 $p^{2}$ 整除，那么它的平方也可以被 $p^{2}$ 整除” 可以通过放宽它的假设来升级：“如果一个数字可以被 $p$ 整除，那么它的平方可以被 $p^{2}$ 整除”，或者通过收紧它的结论来升级：“如果一个数字可以被 $p^{2}$ 整除，那么它的平方可以被 $p^{4}$ 整除”。

其次，在证明了“如果 $P$ 那么 $Q$” 之后，下一步是研究是否存在 $Q$ 成立但 $P$ 不成立的情况。目的是更好地理解 $P$ 和 $Q$ 之间的关系，以便加强命题。

等价

当 $P$ 蕴含 $Q$，以及 $Q$ 蕴含 $P$ 时，条件语句无法得到改进。 有些表达方式包括：“$P$ 当且仅当 $Q$”， “$P$ 当且仅当 $Q$”, “$P$ 和 $Q$ 在逻辑上是等价的”， “$P$ 是得到 $Q$ 的必要和充分条件”， “$P\iff Q$”。 例如，“一个数能被一个素数整除，当且仅当该数的平方能被该素数的平方整除”。

此图表明 $P$ 和 $Q$ 在完全相同的情况下成立。

虽然在简单的论证中，像 “$P$ 当且仅当 $R$，该条件成立，当且仅当 $S$ ...” 这样的链条可能很实用，但通常我们通过分别证明“如果 $P$ 则 $Q$” 和 “如果 $Q$ 则 $P$” 来证明等价性。