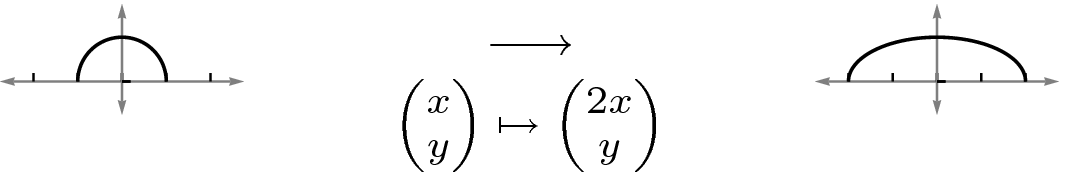线性代数/主题：特征值的几何意义

--参考线性变换几何意义主题---

从基本运算的角度来刻画线性变换在某些方面是不错的（例如，我们可以很容易地看出直线被映射到直线，因为投影、扩张、反射和错切等运算都会将直线映射到直线），但是当一个映射被表示为许多小的运算的复合时——无论这些运算多么简单——其描述都不够理想。我们最后以另一种方式，一种更整体的方式，来描绘$\mathbb {R} ^{2}$变换的几何效应。

该领域中的图片仅仅给出了映射对定义域中一个或两个元素的作用。尽管我们知道一个变换完全由它对基的元素的作用来描述，因此严格来说，描述$\mathbb {R} ^{2}$的变换只需要描述它将任何基的两个向量映射到哪里，但这些图片似乎并没有传达多少几何直觉。我们能否通过添加更多信息来阐明线性映射的几何意义，但又不至于添加太多信息导致图片变得混乱？

一个$\mathbb {R} ^{2}$的变换将过原点的直线映射到过原点的直线。因此，一条直线$y=k_{1}x$上的两点都会被映射到另一条直线上，比如说$y=k_{2}x$。考虑这两点。其中一点是另一点的倍数，因此我们可以用第二点表示为第一点的$r$倍，其中$r$是某个标量。

${\begin{pmatrix}x\\k_{1}x\end{pmatrix}}\quad {\mbox{and}}\quad {\begin{pmatrix}(rx)\\k_{1}(rx)\end{pmatrix}}$

比较它们的像。

${\begin{pmatrix}a&c\\b&d\end{pmatrix}}{\begin{pmatrix}x\\k_{1}x\end{pmatrix}}={\begin{pmatrix}ax+ck_{1}x\\bx+dk_{1}x\end{pmatrix}}\qquad {\begin{pmatrix}a&c\\b&d\end{pmatrix}}{\begin{pmatrix}(rx)\\k_{1}(rx)\end{pmatrix}}={\begin{pmatrix}a(rx)+ck_{1}(rx)\\b(rx)+dk_{1}(rx)\end{pmatrix}}$

第二个向量是第一个向量的$r$倍，第二个向量的像是第一个向量的$r$倍。变换不仅保持了向量共线的性质，还保持了向量的相对比例。也就是说，变换对过原点的直线上的点具有统一的作用。为了描述映射对整条直线的影响，我们只需要描述它对该直线上任意一个非零点的影响。

由于空间中的每个点都位于过原点的某条直线上，为了理解$\mathbb {R} ^{2}$的线性变换的作用，只需从每条过原点的直线上选择一个点（例如单位圆上半部分的点），并展示映射对这组点的作用。

下面是对于一个简单的扩张的这种图片。

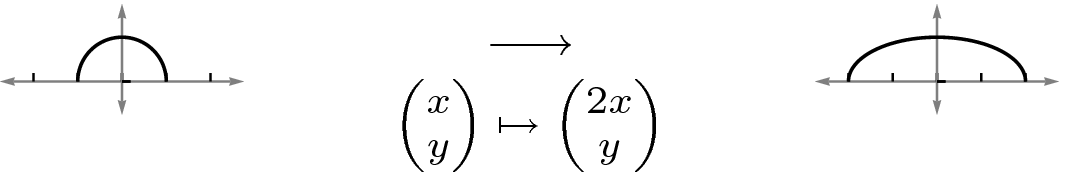
下面，同一个映射用圆及其像叠加在一起显示。

当然，这里的几何关系更加明显。例如，我们可以看到一些过原点的直线实际上被映射到自身：$x$轴被映射到$x$轴，$y$轴被映射到$y$轴。

这是之前显示的翻转，这里叠加了圆及其图像。

这是之前显示的错切。

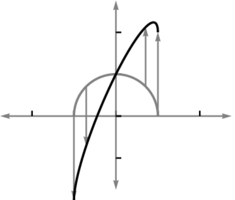
将此映射对单位正方形的影响的图像与这幅图像进行对比。

这是一个稍微复杂一些的映射（第二个坐标函数与前一幅图中的映射相同，但第一个坐标函数不同）。

观察到一些向量正在被同时拉伸和旋转某个角度。

${\begin{pmatrix}x\\2x\end{pmatrix}}\mapsto {\begin{pmatrix}x\\k_{1}x\end{pmatrix}}$

而其他的只是被拉伸，根本没有旋转。

${\begin{pmatrix}x\\3x\end{pmatrix}}\mapsto {\begin{pmatrix}x\\3x\end{pmatrix}}$

练习

问题 1

显示每个矩阵对单位圆上半部分的影响。

1. ${\begin{pmatrix}1&1\\2&2\end{pmatrix}}$
2. ${\begin{pmatrix}2&3\\1&1\end{pmatrix}}$
3. ${\begin{pmatrix}2&3\\1&-1\end{pmatrix}}$

哪些向量保持在过原点的同一条直线上？

解答