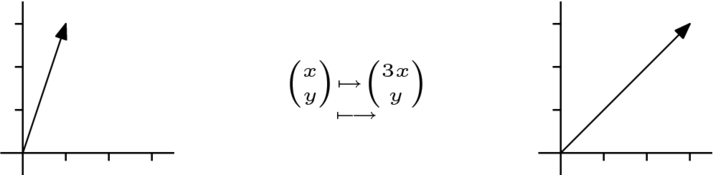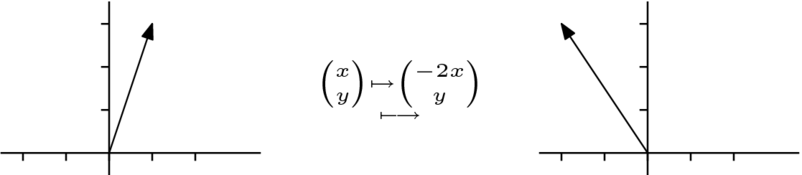下面的图片对比了 和
和  ,它们是非线性的,与
,它们是非线性的,与  和
和  ,它们是线性的。所有四张图片都显示了左侧的定义域
,它们是线性的。所有四张图片都显示了左侧的定义域  映射到右侧的陪域
映射到右侧的陪域  。箭头追踪每个映射发送
。箭头追踪每个映射发送  、
、 、
、 、
、 和
和  的位置。注意非线性映射在将定义域转换为值域时如何扭曲定义域。例如,
的位置。注意非线性映射在将定义域转换为值域时如何扭曲定义域。例如, 比
比  更远离
更远离  ——映射不均匀地扩展了定义域,使得靠近
——映射不均匀地扩展了定义域,使得靠近  的区间在传递到值域时比靠近
的区间在传递到值域时比靠近  的区间扩展得更远。
的区间扩展得更远。
线性映射更友好,更规则,因为对于每个映射,整个定义域都以相同的因子扩展。
从  到
到  的唯一线性映射是乘以一个标量。在更高维度下,可能会发生更多的情况。 例如,这个
的唯一线性映射是乘以一个标量。在更高维度下,可能会发生更多的情况。 例如,这个  的线性变换,将向量逆时针旋转,不仅仅是标量乘法。
的线性变换,将向量逆时针旋转,不仅仅是标量乘法。
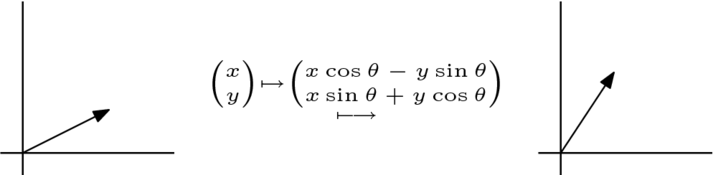
将  中的向量投影到
中的向量投影到  平面上的变换也不是简单的缩放。
平面上的变换也不是简单的缩放。

尽管如此,即使在更高维度下,情况也不会太复杂。
下面,我们使用标准基来表示每个线性映射  为一个矩阵
为一个矩阵  。回想一下,任何
。回想一下,任何  可以分解为
可以分解为  ,其中
,其中  和
和  是非奇异的,而
是非奇异的,而  是一个部分单位矩阵。 此外,回想一下,非奇异矩阵可以分解为初等矩阵
是一个部分单位矩阵。 此外,回想一下,非奇异矩阵可以分解为初等矩阵  ,这些矩阵是从单位矩阵
,这些矩阵是从单位矩阵  通过一个高斯步骤获得的
通过一个高斯步骤获得的
![{\displaystyle I{\xrightarrow[{}]{k\rho _{i}}}M_{i}(k)\qquad I{\xrightarrow[{}]{\rho _{i}\leftrightarrow \rho _{j}}}P_{i,j}\qquad I{\xrightarrow[{}]{k\rho _{i}+\rho _{j}}}C_{i,j}(k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8efb67d5d26695581b1ba19fa3f9d1f49e49f4ed)
( ,
,  ). 因此,如果我们理解由部分单位矩阵描述的线性映射的影响,以及由基本矩阵描述的线性映射的影响,那么在某种程度上,我们将理解任何线性映射的影响。(下面的图片只关注
). 因此,如果我们理解由部分单位矩阵描述的线性映射的影响,以及由基本矩阵描述的线性映射的影响,那么在某种程度上,我们将理解任何线性映射的影响。(下面的图片只关注 的变换,以方便绘制,但这些陈述适用于从任何
的变换,以方便绘制,但这些陈述适用于从任何 到任何
到任何 的映射。)
的映射。)
由部分单位矩阵表示的线性变换的几何效果是投影。

对于 矩阵,由该矩阵表示的变换的几何作用(相对于标准基)是沿
矩阵,由该矩阵表示的变换的几何作用(相对于标准基)是沿 轴将向量拉伸
轴将向量拉伸 倍。该映射沿
倍。该映射沿 轴拉伸了
轴拉伸了 倍。
倍。
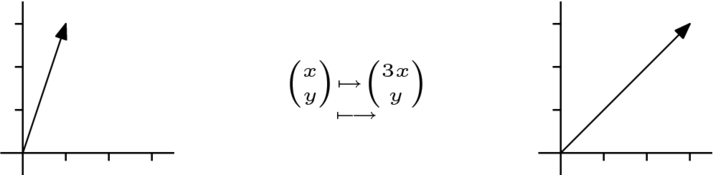
注意,如果 或者如果
或者如果 ,那么
,那么 分量朝另一个方向移动;在这里,朝左侧移动。
分量朝另一个方向移动;在这里,朝左侧移动。
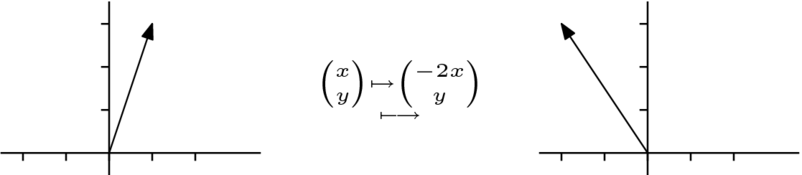
这两个都是伸缩变换。
由 置换矩阵表示的变换的作用是交换
置换矩阵表示的变换的作用是交换 轴和
轴和 轴;这是一种特殊的反射。
轴;这是一种特殊的反射。

在更高维度中,涉及多个轴的置换可以分解为一对轴交换的组合 - 请参见问题 5。
剩下的情况是形式为  的矩阵。回想一下,例如
的矩阵。回想一下,例如  执行
执行  。
。

在下图中,第一个分量为  的向量
的向量  比第一个分量为
比第一个分量为  的向量
的向量  受到的影响更小——
受到的影响更小——  只比
只比  高
高  ,而
,而  比
比  高
高  。
。

任何第一个分量为  的向量都会受到影响,就像
的向量都会受到影响,就像  一样;它会向上滑动
一样;它会向上滑动  。任何第一个分量为
。任何第一个分量为  的向量会向上滑动
的向量会向上滑动  ,就像
,就像  一样。也就是说,由
一样。也就是说,由  表示的变换会影响向量,具体取决于它们的
表示的变换会影响向量,具体取决于它们的  个分量。
个分量。
从另一个角度看,可以考虑此映射对单位正方形的作用。在下图中,第一个分量为  的向量,例如原点,在垂直方向上没有移动,但第一个分量为正值的向量会向上移动。在这里,所有第一个分量为
的向量,例如原点,在垂直方向上没有移动,但第一个分量为正值的向量会向上移动。在这里,所有第一个分量为  的向量——即正方形的整个右侧——都会受到相同程度的影响。更一般地说,位于同一垂线的向量会向上移动相同的距离,即它们向上移动的距离是其第一个分量的两倍。由此产生的形状(菱形)与正方形具有相同的底和高(因此面积相同),但直角消失了。
的向量——即正方形的整个右侧——都会受到相同程度的影响。更一般地说,位于同一垂线的向量会向上移动相同的距离,即它们向上移动的距离是其第一个分量的两倍。由此产生的形状(菱形)与正方形具有相同的底和高(因此面积相同),但直角消失了。

作为对比,下一张图片展示了由  表示的映射所产生的影响。在这种情况下,向量会根据其第二个分量受到影响。向量
表示的映射所产生的影响。在这种情况下,向量会根据其第二个分量受到影响。向量  会水平移动
会水平移动  的两倍。
的两倍。

由于这种作用,这种映射被称为 **剪切**。
至此,我们已经涵盖了扩张中四种类型组件的几何效应 ,部分恒等投影
,部分恒等投影 和基本
和基本 。由于我们理解其组成部分,在某种意义上,我们也理解任何
。由于我们理解其组成部分,在某种意义上,我们也理解任何 的作用。为了说明这一断言,回想一下,在一次线性映射下,子空间的像是一个子空间,因此由
的作用。为了说明这一断言,回想一下,在一次线性映射下,子空间的像是一个子空间,因此由 表示的线性变换
表示的线性变换 将过原点的直线映射到过原点的直线。(像空间的维数不能大于定义域空间的维数,因此直线不能映射到例如平面。)我们将扩展这一点,证明任何直线,而不仅仅是过原点的直线,都会被
将过原点的直线映射到过原点的直线。(像空间的维数不能大于定义域空间的维数,因此直线不能映射到例如平面。)我们将扩展这一点,证明任何直线,而不仅仅是过原点的直线,都会被 映射到一条直线。证明很简单,部分恒等投影
映射到一条直线。证明很简单,部分恒等投影 和基本
和基本 每次将直线输入转换为直线输出(验证这四种情况是问题 6),因此它们的组合也保留了直线。因此,通过理解其组成部分,我们可以理解任意方阵
每次将直线输入转换为直线输出(验证这四种情况是问题 6),因此它们的组合也保留了直线。因此,通过理解其组成部分,我们可以理解任意方阵 ,因为我们可以证明关于它们的性质。
,因为我们可以证明关于它们的性质。
理解线性变换对 的几何效应在数学中非常重要。以下是一个来自微积分的熟悉应用。左侧是非线性函数
的几何效应在数学中非常重要。以下是一个来自微积分的熟悉应用。左侧是非线性函数 作用的图像。正如本主题开头所述,总体而言,该映射的几何效应是不规则的,因为在不同的定义域点上它具有不同的效应(例如,随着定义域点
作用的图像。正如本主题开头所述,总体而言,该映射的几何效应是不规则的,因为在不同的定义域点上它具有不同的效应(例如,随着定义域点 从
从 变为
变为 ,相关的值域点
,相关的值域点 开始下降,然后瞬间暂停,然后上升)。
开始下降,然后瞬间暂停,然后上升)。
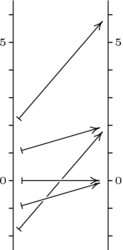
但在微积分中,我们不关注整个映射,而是关注映射的局部效应。
在 处,导数为
处,导数为 ,因此在
,因此在 附近,我们有
附近,我们有 。
。
也就是说,在  的邻域内,当将定义域映射到值域时,该映射会使值域增大
的邻域内,当将定义域映射到值域时,该映射会使值域增大  倍——在局部范围内,它近似于一个伸缩变换。
倍——在局部范围内,它近似于一个伸缩变换。
下图显示了定义域中  的一个小区间,它被映射到值域中
的一个小区间,它被映射到值域中  的一个区间,该区间宽度是前者的三倍:
的一个区间,该区间宽度是前者的三倍: 。
。

(当以上图形以传统的笛卡尔坐标系方式绘制时,关于  增速的上述句子通常会被表述为:导数
增速的上述句子通常会被表述为:导数  给出了该点
给出了该点  的切线的斜率。)
的切线的斜率。)
在更高维度中,这个想法是一样的,但是近似值不仅仅是  到
到  的标量乘法情况。相反,对于一个函数
的标量乘法情况。相反,对于一个函数  和一个点
和一个点  ,导数被定义为一个线性映射
,导数被定义为一个线性映射  ,它最能近似地描述
,它最能近似地描述  在
在  附近的变化方式。因此,上述研究的几何学也适用于这种情况。
附近的变化方式。因此,上述研究的几何学也适用于这种情况。
我们将通过说明这种观点如何使人们清楚地认识到一个关于导数的常常被误解但非常重要的结果来结束本主题:两个函数的复合函数的导数可以通过使用链式法则来组合它们的导数来计算。请记住(当两个函数满足适当条件时)

例如, 的导数是
的导数是  。这个组合是如何产生的呢?从复合函数作用的图示可以看出来。
。这个组合是如何产生的呢?从复合函数作用的图示可以看出来。
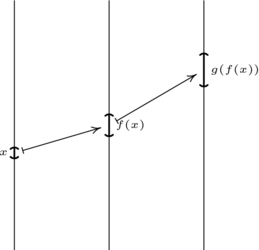
第一个映射  将
将  附近的邻域按
附近的邻域按

的因子进行膨胀,而第二个映射  将
将  附近的邻域按
附近的邻域按

的因子进行膨胀,因此,复合函数按这两个因子的乘积进行膨胀。
在更高维空间中,表示函数在某点附近变化的映射是一个线性映射,它可以用矩阵表示。(因此,我们理解了高维导数的基本几何意义;它们是膨胀、轴交换、剪切和投影的组合)。链式法则只是将这些矩阵相乘。
因此,线性映射  的几何意义既简单又实用。
的几何意义既简单又实用。
- 问题 2
伸缩、翻转、斜切和投影的什么组合产生了逆时针旋转  弧度?
弧度?
- 问题 3
伸缩、翻转、斜切和投影的什么组合产生了映射  ,该映射由该矩阵相对于标准基表示?
,该映射由该矩阵相对于标准基表示?

- 问题 4
证明  的任何线性变换都是乘以标量
的任何线性变换都是乘以标量  的映射。
的映射。
- 问题 7
使用链式法则讨论中出现的类似图片来回答:如果函数 有逆函数,那么该函数(局部,近似)如何膨胀空间,以及它的逆函数如何膨胀空间之间存在什么关系(当然,假设它有逆函数)?
有逆函数,那么该函数(局部,近似)如何膨胀空间,以及它的逆函数如何膨胀空间之间存在什么关系(当然,假设它有逆函数)?
解答



















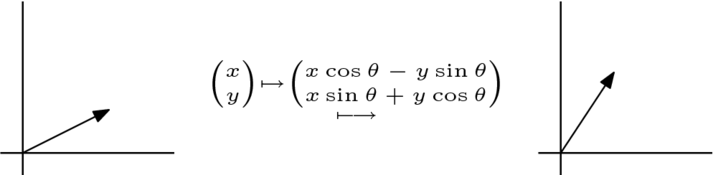











![{\displaystyle I{\xrightarrow[{}]{k\rho _{i}}}M_{i}(k)\qquad I{\xrightarrow[{}]{\rho _{i}\leftrightarrow \rho _{j}}}P_{i,j}\qquad I{\xrightarrow[{}]{k\rho _{i}+\rho _{j}}}C_{i,j}(k)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8efb67d5d26695581b1ba19fa3f9d1f49e49f4ed)