线性代数/主题:线性映射的几何/解答
- 问题 1
令 为将向量顺时针旋转 弧度的变换。
- 找到矩阵,它表示 相对于标准基。使用高斯消元法将 化简为单位矩阵。
- 将行化简转化为矩阵方程(前一项表明 与 相似,并且从 推导出 不需要任何列运算)。
- 解此矩阵方程求。
- 绘制几何效果矩阵,即绘制 如何表示为拉伸、翻转、错切和投影的组合(单位矩阵是平凡的投影)。
- 解答
- 为了表示,回想一下,逆时针旋转 弧度相对于标准基的表示方式如下。
- 这个消元可以用矩阵乘法表示为
- 取逆
- 从右到左阅读组合(并将单位矩阵忽略为平凡的)得出, 的效果与先执行这种倾斜相同
接着进行一个扩张,将所有第一分量乘以 (由于 ,所以这是一个“缩小”),并将所有第二分量乘以 ,接着进行另一个倾斜。
例如, 对与 轴夹角为 的单位向量的效果是
验证得到的向量具有单位长度,并且与 轴的夹角为 是例行公事。
- 问题 2
什么组合的扩张、翻转、倾斜和投影产生逆时针旋转 弧度?
- 解答
我们将首先用矩阵 表示映射,执行行操作,如果需要,则执行列操作以将其简化为部分单位矩阵。然后,我们将将其转换为分解 。代入一般矩阵
给出这种表示。
高斯消元法是常规方法。
这可以以矩阵方程的形式表示。
求逆矩阵来解,得到以下分解。
- 问题 3
什么组合的缩放、翻转、错切和投影操作可以生成由以下矩阵表示的映射?
- 解答
以下高斯消元操作
给出了矩阵的简化行阶梯形式。现在,将第一列乘以 并加到第二列,然后交换第二列和第三列,可以得到这个部分单位矩阵。
所有这些都可以用矩阵形式表示为:其中
和
给出的矩阵可以分解为 。
- 问题 4
证明任何对 的线性变换都是乘以一个标量 的映射。
- 解答
用标准基 表示它,那么得到的 矩阵中唯一的元素就是标量 。
- 问题 5
证明对于数字 ,..., 的任何排列(即重新排序),映射
可以通过一系列映射的复合来实现,其中每个映射只交换一对坐标。提示:可以用关于 的归纳法来证明。(注:在第四章中我们将证明这一点,并将证明所用交换次数的奇偶性由 决定。也就是说,虽然特定排列可以用两种不同的方式实现,但两种方式所用的交换次数不同,但两种方式要么都用偶数次交换,要么都用奇数次交换。)
- 解答
我们可以用关于向量分量个数的归纳法来证明这一点。在 的基本情况中,唯一可能的排列是平凡排列,映射
实际上可以用一系列交换来表示——可以表示为零次交换。对于归纳步骤,我们假设由少于 个数字的任何排列引起的映射,都可以仅用交换来表示。现在我们考虑由 引起的映射,其中 是 个数字的排列。
考虑一个数字 ,使得 。映射
如果接着交换第 个和第 个分量,就会得到映射 。现在,归纳假设表明 可以通过一系列交换来实现。
- 问题 6
证明线性映射保持空间的线性结构。
- 证明对于从 到 的任何线性映射,任何直线的像都是直线。像可能是一个退化的直线,即一个点。
- 证明任何线性曲面的像都是线性曲面。这推广了线性映射下子空间的像也是子空间的结果。
- 线性映射保持其他线性概念。证明线性映射保持“介于”:如果点 介于 和 之间,那么 的像介于 的像和 的像之间。
- 解答
- 一条直线是 的一个子集,其形式为 。该直线上一点的图像为 ,并且当 在实数范围内变化时,这些向量的集合是一条直线(如果 ,则该直线为退化的)。
- 这是一个对之前论点的明显扩展。
- 如果点 在点 和 之间,那么从 到 的直线上包含 。也就是说,存在一个 使得 (其中 是 的端点,等等)。现在,如同第一个条目的论证,线性性表明 .










![{\displaystyle {\xrightarrow[{}]{\rho _{1}+\rho _{2}}}{\begin{pmatrix}{\sqrt {2}}/2&{\sqrt {2}}/2\\0&{\sqrt {2}}\end{pmatrix}}{\xrightarrow[{(1/{\sqrt {2}})\rho _{2}}]{(2/{\sqrt {2}})\rho _{1}}}{\begin{pmatrix}1&1\\0&1\end{pmatrix}}{\xrightarrow[{}]{-\rho _{2}+\rho _{1}}}{\begin{pmatrix}1&0\\0&1\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faae28eb7d6e867ffd9a39f73f6bcf2b569fbd03)







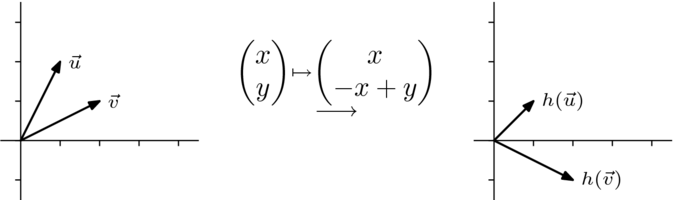


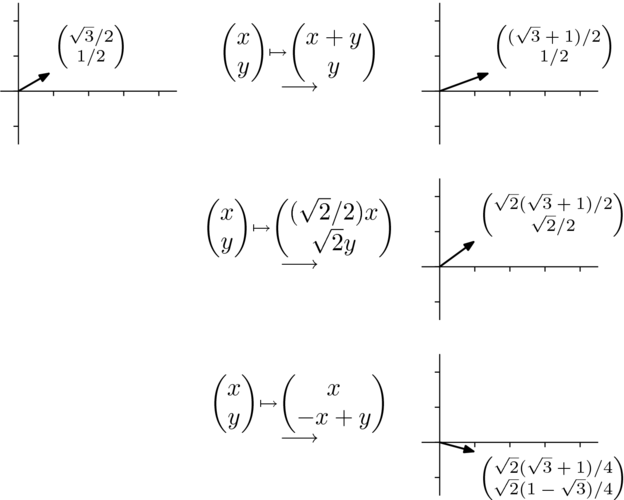





![{\displaystyle {\xrightarrow[{}]{{\sqrt {3}}\rho _{1}+\rho _{2}}}{\begin{pmatrix}-1/2&-{\sqrt {3}}/2\\0&-2\end{pmatrix}}{\xrightarrow[{(-1/2)\rho _{2}}]{-2\rho _{1}}}{\begin{pmatrix}1&{\sqrt {3}}\\0&1\end{pmatrix}}{\xrightarrow[{}]{-{\sqrt {3}}\rho _{2}+\rho _{1}}}{\begin{pmatrix}1&0\\0&1\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/443d4da6f31b7426c5d7799df1864905b916611c)




![{\displaystyle {\xrightarrow[{-\rho _{1}+\rho _{3}}]{-3\rho _{1}+\rho _{2}}}{\begin{pmatrix}1&2&1\\0&0&-3\\0&0&1\end{pmatrix}}{\xrightarrow[{}]{(1/3)\rho _{2}+\rho _{3}}}{\begin{pmatrix}1&2&1\\0&0&-3\\0&0&0\end{pmatrix}}{\xrightarrow[{}]{(-1/3)\rho _{2}}}{\begin{pmatrix}1&2&1\\0&0&1\\0&0&0\end{pmatrix}}{\xrightarrow[{}]{-\rho _{2}+\rho _{1}}}{\begin{pmatrix}1&2&0\\0&0&1\\0&0&0\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0abe27d67c8beb79e1da4544e0b32614f3655bb8)






































