线性代数/主题：投票悖论/解决方案

解决方案

问题 1

这里有一个合理的投票者可能拥有循环偏好的方式。假设此投票者根据三个标准对每个候选人进行排名。

1. 制作一个表格，行标签为“民主党”、“共和党”和“第三党”，列标签为“品格”、“经验”和“政策”。在每一列中，将某个候选人排为最受欢迎，将另一个排为中间，并将剩下的排为最不受欢迎。
2. 在这个排名中，民主党在（至少）三个标准中的两个标准上是否比共和党更受欢迎，反之亦然？共和党是否比第三党更受欢迎？
3. 刚刚构建的表格是否具有循环偏好顺序？如果没有，请创建一个具有循环偏好顺序的表格。

因此，投票者可能对候选人具有循环偏好。然而，上面描述的悖论是，即使每个投票者都有一个直线偏好列表，整个群体仍然可能出现循环偏好。

答案

这是一个导致单个投票者非理性偏好顺序的示例。

	品格	经验	政策
民主党	最受欢迎	中间	最不受欢迎
共和党	中间	最不受欢迎	最受欢迎
第三党	最不受欢迎	最受欢迎	中间

民主党在品格和经验方面比共和党更受欢迎。共和党在品格和政策方面比第三党更受欢迎。而第三党在经验和政策方面比民主党更受欢迎。

问题 2

计算分解表中的值。

答案

首先，将$D>R>T$分解与主题中完成的相反$T>R>D$投票者的分解进行比较。

${\begin{pmatrix}-1\\1\\1\end{pmatrix}}={\frac {1}{3}}\cdot {\begin{pmatrix}1\\1\\1\end{pmatrix}}+{\frac {2}{3}}\cdot {\begin{pmatrix}-1\\1\\0\end{pmatrix}}+{\frac {2}{3}}\cdot {\begin{pmatrix}-1\\0\\1\end{pmatrix}}\quad {\text{and}}\quad {\begin{pmatrix}1\\-1\\-1\end{pmatrix}}=d_{1}\cdot {\begin{pmatrix}1\\1\\1\end{pmatrix}}+d_{2}\cdot {\begin{pmatrix}-1\\1\\0\end{pmatrix}}+d_{3}\cdot {\begin{pmatrix}-1\\0\\1\end{pmatrix}}$

显然，第二个是第一个的负数，所以$d_{1}=-1/3$, $d_{2}=-2/3$, 以及$d_{3}=-2/3$。此原则适用于任何一对相反的投票者，因此我们只需对第二行的一个投票者和第三行的一个投票者进行计算。对于第二行中的正向投票者，

${\begin{array}{*{3}{rc}r}c_{1}&-&c_{2}&-&c_{3}&=&1\\c_{1}&+&c_{2}&&&=&1\\c_{1}&&&+&c_{3}&=&-1\end{array}}\;{\xrightarrow[{-\rho _{1}+\rho _{3}}]{-\rho _{1}+\rho _{2}}}\;{\xrightarrow[{}]{(-1/2)\rho _{2}+\rho _{3}}}\;{\begin{array}{*{3}{rc}r}c_{1}&-&c_{2}&-&c_{3}&=&1\\&&2c_{2}&+&c_{3}&=&0\\&&&&(3/2)c_{3}&=&-2\end{array}}$

给出 $c_{3}=-4/3$，$c_{2}=2/3$，以及 $c_{1}=1/3$。对于第三行中的一个正面投票者，

${\begin{array}{*{3}{rc}r}c_{1}&-&c_{2}&-&c_{3}&=&1\\c_{1}&+&c_{2}&&&=&-1\\c_{1}&&&+&c_{3}&=&1\end{array}}\;{\xrightarrow[{-\rho _{1}+\rho _{3}}]{-\rho _{1}+\rho _{2}}}\;{\xrightarrow[{}]{(-1/2)\rho _{2}+\rho _{3}}}\;{\begin{array}{*{3}{rc}r}c_{1}&-&c_{2}&-&c_{3}&=&1\\&&2c_{2}&+&c_{3}&=&-2\\&&&&(3/2)c_{3}&=&1\end{array}}$

给出 $c_{3}=2/3$，$c_{2}=-4/3$，以及 $c_{1}=1/3$。

问题 3

对于政治学班的模拟选举，是否发生了相反偏好排序的抵消？剩下的偏好是来自表格的前三行还是后三行？

答案

模拟选举对应于上面投票偏好表中显示的方式，抵消之后的结果是第二张表。

正面倾向     负面倾向     $D>R>T$   5 票   $T>R>D$   2 票   $R>T>D$   8 票   $D>T>R$   4 票   $T>D>R$   8 票   $R>D>T$   2 票

正面倾向     负面倾向     $D>R>T$   3 票   $T>R>D$   –   $R>T>D$   4 票   $D>T>R$   –   $T>D>R$   6 票   $R>D>T$   –

所有三者都来自桌子的同一侧（左侧），正如本主题的结果所说必须发生的那样。现在可以使用取消的数字进行选举计票

$3\cdot \,$ $+4\cdot \,$$+6\cdot$$\,=\,$

得到相同的结果。

问题 4

上面证明的必要条件——投票悖论只有在取消后剩余的所有三个偏好列表具有相同旋转时才会发生——不是充分的。

1. 继续证明中考虑的正循环情况，使用两个不等式 $0\leq a-b+c$ 和 $0\leq -a+b+c$ 来证明 $|a-b|\leq c$.
2. 还需证明 $c\leq a+b$，因此 $|a-b|\leq c\leq a+b$.
3. 举一个投票的例子，其中存在多数循环，并且添加一个具有相同旋转的投票者会导致循环消失。
4. 相反的情况会发生吗？添加一个具有“错误”旋转的投票者会导致循环出现吗？
5. 给出获得多数循环的必要且充分的条件。

答案

1. 这两个可以改写成 $-c\leq a-b$ 和 $-c\leq b-a$。无论是 $a-b$ 还是 $b-a$ 都是非正数，因此 $-c\leq -|a-b|$，如所要求的。
2. 这是从假设 $0\leq a+b-c$ 中直接得出的。
3. 一个简单的例子是从零选民选举开始，然后添加任何一个选民。一个更有趣的例子是，取政治学模拟选举，并添加两个 $T>D>R$ 选民（他们可以一次添加一个，以满足问题中“添加一个选民”的标准）。观察到，这些额外的选民具有正旋度，这与原始模拟选举中抵消后剩余的票数的旋度相同。这是选民的表格结果，旁边是抵消后的结果。

   正面倾向     负面倾向     $D>R>T$   5 票   $T>R>D$   2 票   $R>T>D$   8 票   $D>T>R$   4 票   $T>D>R$   10 位选民   $R>D>T$   2 票

   正面倾向     负面倾向     $D>R>T$   3 票   $T>R>D$   –   $R>T>D$   4 票   $D>T>R$   –   $T>D>R$   8 票   $R>D>T$   –

   使用抵消后的数字的选举结果如下。

   $3\cdot \,$$\,+4\cdot \,$$\,+8\cdot \,$$\,=\,$

   多数循环确实消失了。

4. 其中一个条件是，抵消后，所有三个值都为非负数，或者所有三个值都为非正数，并且：$|c|<|a+b|$ 和 $|b|<|a+c|$ 和 $|a|<|b+c|$。这是从下图得出的。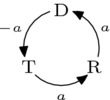

   $\,+\,$$\,+\,$$\,=\,$

问题 5

由于我们要求投票者的列表必须是合理的，因此单人投票选举不可能出现多数循环。

1. 证明双人投票选举可能出现多数循环。（如果所有三个组的总数都为非负数或所有三个组的总数都为非正数，则我们认为群体偏好为多数循环——也就是说，我们允许群体偏好中存在零。）
2. 证明对于任何大于 1 的投票人数，存在涉及该人数投票的选举，从而导致多数循环。

答案

1. 双人投票选举可以通过两种方式出现多数循环。首先，这两个投票者可以是相反的，在抵消后导致平凡选举（所有为零的多数循环）。其次，这两个投票者可以有相同的旋转，但来自不同的行，如这里所示。

   $1\cdot \,$$\,+1\cdot \,$$\,+0\cdot \,$$\,=\,$

2. 有两种情况。偶数个投票者可以平均分成相反的两个部分，例如，一半投票者是 $D>R>T$ 另一半是 $T>R>D$。然后抵消得到平凡选举。如果投票人数大于 1 且为奇数（形如 $2k+1$ 其中 $k>0$）那么使用证明中的循环图，

   $\,+\,$$\,+\,$$\,=\,$

   我们可以取 $a=k$ 和 $b=k$ 以及 $c=1$。因为 $k>0$，这是一个多数循环。

问题 6

令 $U$ 是 $\mathbb {R} ^{3}$ 的一个子空间。证明向量集合 $U^{\perp }=\{{\vec {v}}\,{\big |}\,{\vec {v}}\cdot {\vec {u}}=0{\text{ for all }}{\vec {u}}\in U\}$，即与 $U$ 中每个向量垂直的向量，也是 $\mathbb {R} ^{3}$ 的一个子空间。

答案

它是非空的，因为它包含零向量。为了证明它在两个成员的线性组合下是封闭的，假设 ${\vec {v}}_{1}$ 和 ${\vec {v}}_{2}$ 在 $U^{\perp }$ 中，并考虑 $c_{1}{\vec {v}}_{1}+c_{2}{\vec {v}}_{2}$。对于任何 ${\vec {u}}\in U$，

$(c_{1}{\vec {v}}_{1}+c_{2}{\vec {v}}_{2})\cdot {\vec {u}}=c_{1}({\vec {v}}_{1}\cdot {\vec {u}})+c_{2}({\vec {v}}_{2}\cdot {\vec {u}})=c_{1}\cdot 0+c_{2}\cdot 0=0$

因此 $c_{1}{\vec {v}}_{1}+c_{2}{\vec {v}}_{2}\in U^{\perp }$.