线性代数/主题：投票悖论

线性代数
← 主题：晶体	主题：投票悖论	主题：量纲分析 →

想象一下，一个学习美国总统选举过程的政治学班级举行了一次模拟选举。学生被要求按从最喜欢到最不喜欢的顺序，对来自民主党、共和党和第三党的候选人进行排名，结果如下 ( $>$ 表示“比……更受欢迎”)。

偏好顺序	具有该偏好的人数
民主党 > 共和党 > 第三党	5
民主党 > 第三党 > 共和党	4
共和党 > 民主党 > 第三党	2
共和党 > 第三党 > 民主党	8
第三党 > 民主党 > 共和党	8
第三党 > 共和党 > 民主党	2
总计	29

整个群体对候选人的偏好是什么？

总体而言，该群体对民主党比共和党更喜爱，共五票之差；17 名选民将民主党排在共和党之上，而 12 名选民则相反。而且，该群体总体上更喜爱共和党人而不是第三党的候选人，共 15 票对 14 票。但是，奇怪的是，该群体也更喜爱第三党人而不是民主党人，共 18 票对 11 票。

‎

这是一个投票悖论的例子，具体来说，是一个多数循环。

对投票悖论的研究部分是因为它们对实际政治的影响。例如，老师可以通过首先让班级在共和党和第三党之间选择，然后再让班级在该竞赛的获胜者（共和党）和民主党之间选择，从而操纵班级选择民主党为总体获胜者。通过类似的操纵，其他两名候选人中的任何一个都可以成为获胜者。（在本主题中，我们将坚持三名候选人的选举，但类似的结果适用于更大的选举。）

投票悖论也仅仅因为它们在数学上很有趣而被研究。一个有趣的地方是，尽管每个选民的偏好列表都是理性的——以直线的顺序排列，但该群体整体上的多数循环仍然发生了。也就是说，多数循环似乎是在聚合中产生的，而没有出现在聚合的元素（偏好列表）中。然而，最近，线性代数被用来 (Zwicker 1991) 论证，实际上每个选民的列表中都存在着循环偏好的趋势，并且当这种趋势的加总比抵消多时，它就会显现出来。

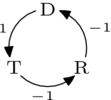
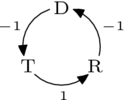
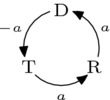
为了论证这一点，将选项简写为 $D$ 、 $R$ 和 $T$ ，我们可以描述一个偏好顺序为 $D>R>T$ 的选民是如何对上述循环做出贡献的。

(负号在这里是因为箭头描述的是 $T$ 比 $D$ 更受欢迎，但该选民更喜欢它们的反方向。) 其他偏好列表的描述在下面的投票偏好表格中。

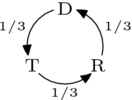
现在，要进行选举，我们将这些描述线性组合起来；例如，政治学模拟选举

5\cdot \,

\,+4\cdot \,

\,+\cdots +2\cdot \,

产生了前面显示的循环群体偏好。

当然，取线性组合属于线性代数。上面的循环记号具有提示性，但并不方便，因此我们暂时切换到使用列向量，从 $D$ 开始，并以逆时针方向取循环中的数字。因此，模拟选举和单个 $D>R>T$ 投票将以这种方式表示。

{\begin{pmatrix}7\\1\\5\end{pmatrix}}\quad {\text{and}}\quad {\begin{pmatrix}-1\\1\\1\end{pmatrix}}

我们将把投票向量分解成两部分，一部分是循环的，另一部分是非循环的。对于第一部分，我们说一个向量是纯循环的，如果它在这个子空间中 $\mathbb {R} ^{3}$ .

C=\{{\begin{pmatrix}k\\k\\k\end{pmatrix}}\,{\big |}\,k\in \mathbb {R} \}=\{k\cdot {\begin{pmatrix}1\\1\\1\end{pmatrix}}\,{\big |}\,k\in \mathbb {R} \}

对于第二部分，考虑子空间（参见问题 6），该子空间包含与 $C$ 中所有向量垂直的向量。

C^{\perp }=\{{\begin{pmatrix}c_{1}\\c_{2}\\c_{3}\end{pmatrix}}\,{\big |}\,{\begin{pmatrix}c_{1}\\c_{2}\\c_{3}\end{pmatrix}}\cdot {\begin{pmatrix}k\\k\\k\end{pmatrix}}=0{\text{ for all }}k\in \mathbb {R} \}

=\{{\begin{pmatrix}c_{1}\\c_{2}\\c_{3}\end{pmatrix}}\,{\big |}\,c_{1}+c_{2}+c_{3}=0\}=\{c_{2}{\begin{pmatrix}-1\\1\\0\end{pmatrix}}+c_{3}{\begin{pmatrix}-1\\0\\1\end{pmatrix}}\,{\big |}\,c_{2},c_{3}\in \mathbb {R} \}

(读作“ $C$ 垂直”。）因此，我们得到了 $\mathbb {R} ^{3}$ 的这个基。

\langle {\begin{pmatrix}1\\1\\1\end{pmatrix}},{\begin{pmatrix}-1\\1\\0\end{pmatrix}},{\begin{pmatrix}-1\\0\\1\end{pmatrix}}\rangle

我们可以根据这个基表示投票，从而将投票分解为循环部分和非循环部分。（对于学习过本章可选章节的读者注意：即，空间是 $C$ 和 $C^{\perp }$ 的直和。）

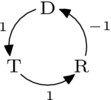
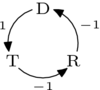
例如，考虑上面讨论的 $D>R>T$ 投票者。用基表示很容易找到，

{\begin{array}{rcl}{\begin{array}{*{3}{rc}r}c_{1}&-&c_{2}&-&c_{3}&=&-1\\c_{1}&+&c_{2}&&&=&1\\c_{1}&&&+&c_{3}&=&1\end{array}}&{\xrightarrow[{-\rho _{1}+\rho _{3}}]{-\rho _{1}+\rho _{2}}}\;{\xrightarrow[{}]{(-1/2)\rho _{2}+\rho _{3}}}&{\begin{array}{*{3}{rc}r}c_{1}&-&c_{2}&-&c_{3}&=&-1\\&&2c_{2}&+&c_{3}&=&2\\&&&&(3/2)c_{3}&=&1\end{array}}\end{array}}

因此 $c_{1}=1/3$ ， $c_{2}=2/3$ ，以及 $c_{3}=2/3$ 。然后

{\begin{pmatrix}-1\\1\\1\end{pmatrix}}={\frac {1}{3}}\cdot {\begin{pmatrix}1\\1\\1\end{pmatrix}}+{\frac {2}{3}}\cdot {\begin{pmatrix}-1\\1\\0\end{pmatrix}}+{\frac {2}{3}}\cdot {\begin{pmatrix}-1\\0\\1\end{pmatrix}}={\begin{pmatrix}1/3\\1/3\\1/3\end{pmatrix}}+{\begin{pmatrix}-4/3\\2/3\\2/3\end{pmatrix}}

给出循环部分和非循环部分的期望分解。

\,=\,

\,+\,

因此，这个 $D>R>T$ 选民的理性偏好列表确实可以被看作具有一个循环部分。

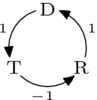
这个 $T>R>D$ 选民与我们刚才考虑的选民相反，因为 " $>$ " 符号颠倒了。这个选民的分解

$\,=\,$ $\,+\,$

表明这些相反的偏好具有相反的分解。我们说第一个选民具有正的**自旋**，因为循环部分与我们为箭头选择的方向一致，而第二个选民的自旋为负。

这些相反的选民互相抵消的事实反映在他们的投票向量加起来为零的事实。这表明了一种计算选举结果的替代方法。我们可以先尽可能地抵消相反的偏好列表，然后通过添加剩下的列表来确定结果。

下表中的行包含三对相反的偏好列表。列根据自旋对这些对进行分组。例如，第一行包含我们刚刚考虑的两个选民。

投票偏好
正号	负自旋
民主党 > 共和党 > 第三方 $\,=\,$ $\,+\,$	第三 > 共和党 > 民主党 $\,=\,$ $\,+\,$
共和党 > 第三 > 民主党 $\,=\,$ $\,+\,$	民主党 > 第三 > 共和党 $\,=\,$ $\,+\,$
第三 > 民主党 > 共和党 $\,=\,$ $\,+\,$	共和党 > 民主党 > 第三方 $\,=\,$ $\,+\,$

如果我们像上面描述的那样进行选举，那么在尽可能多地取消相反的投票对后，将剩下三组偏好列表，一组来自第一行，一组来自第二行，一组来自第三行。我们将最后证明，只有当这三组的自旋方向一致时，才会出现投票悖论。也就是说，为了出现投票悖论，这三个剩余的集合必须全部来自表格的左侧或全部来自右侧（见问题 3）。这表明，多数循环与我们使用的分解之间存在某种联系——只有当循环偏好的趋势相互强化时，才会出现投票悖论。

为了证明，假设已经取消了相反的偏好顺序，并且我们从三行中的每一行都剩下了一组偏好列表。考虑这三个的总和（这里，数字 $a$ ， $b$ ，和 $c$ 可以是正数、负数或零）。

\,+\,

\,+\,

\,=\,

当右边的三个数字 $a-b+c$ 、 $a+b-c$ 和 $-a+b+c$ 都是非负数或都是非正数时，就会出现投票悖论。在左边，三个数字中的至少两个， $a$ 和 $b$ 以及 $c$ ，都是非负数或都是非正数。我们可以假设它们是 $a$ 和 $b$ 。这使得有四种情况：循环是非负数，并且 $a$ 和 $b$ 是非负数，循环是非正数，并且 $a$ 和 $b$ 是非正数等等。我们只做第一种情况，因为第二种情况类似，而另外两种情况也很容易。

所以假设循环是非负数，并且 $a$ 和 $b$ 是非负数。条件 $0\leq a-b+c$ 和 $0\leq -a+b+c$ 相加得到 $0\leq 2c$ ，这意味着 $c$ 也是非负数，如预期的那样。这结束了证明。

这个结果只说明，所有三个旋转都朝同一方向是一个多数循环的必要条件。它不是充分的；见问题 4。

投票理论及其相关主题是当前研究的课题。有许多有趣的成果，最引人注目的成果是由 K. Arrow 提出的 (Arrow 1963)，他因这部分工作而获得了诺贝尔奖，表明没有投票系统是完全公平的（对于“公平”的合理定义而言）。有关更多信息，一些好的入门文章是 (Gardner 1970)、(Gardner 1974)、(Gardner 1980) 和 (Neimi & Riker 1976)。最近的一本相当易读的书籍是 (Taylor 1995)。在 (Poundstone 2008) 中给出的来自美国政治史的众多案例表明，在实践中操纵这些悖论是司空见惯的事情（并且作者提出了一种解决方案）。

本主题主要摘自 (Zwicker 1991)。（作者注：我要感谢 Zwicker 教授的友好和富有启发性的讨论。）

练习

问题 1

这是一个投票者可能具有循环偏好的合理方式。假设该投票者根据三个标准对每个候选人进行排名。

创建一个表格，其中行标为“民主党”、“共和党”和“第三党”，列标为“品格”、“经验”和“政策”。在每列中，将某个候选人排名为最受欢迎，将另一个候选人排名为中等，并将剩下的候选人排名为最不受欢迎。
在这个排名中，民主党是否在（至少）三个标准中的两个标准中优于共和党，反之亦然？共和党是否优于第三党？
刚刚构建的表格是否有循环偏好顺序？如果没有，请创建一个有循环偏好顺序的表格。

因此，投票者可能在候选人之间具有循环偏好。然而，上面描述的悖论是，即使每个投票者都拥有一个直线偏好列表，整个群体仍然可能出现循环偏好。

问题 2

计算分解表格中的值。

问题 3

对政治学课程模拟选举进行相反偏好顺序的抵消。所有剩余的偏好是否都来自表格的左三行或来自右边？

问题 4

上面证明的必要条件——投票悖论仅在抵消后剩余的所有三个偏好列表具有相同的旋转方向时才会发生——不是也充分的。

继续在证明中考虑的正循环情况，使用两个不等式 $0\leq a-b+c$ 和 $0\leq -a+b+c$ 来证明 $|a-b|\leq c$ 。
还要证明 $c\leq a+b$ ，因此证明 $|a-b|\leq c\leq a+b$ 。
给出一个有多数循环的投票示例，以及添加一个具有相同旋转方向的投票者导致循环消失的情况。
是否可能发生相反的情况；添加一个具有“错误”旋转方向的投票者会导致循环出现？
给出一个既必要又充分的条件来获得多数循环。

问题 5: 单人投票选举不可能有多数循环，因为我们规定了投票者列表必须是理性的。

证明二人投票选举可能具有多数循环。（如果所有三个组总和非负，或者所有三个组总和非正，我们认为群体偏好是多数循环——也就是说，我们允许群体偏好中的一些为零。）
证明对于大于 1 的任何投票者数量，都存在一个涉及该数量投票者的选举，其结果是多数循环。

问题 6

令 $U$ 是 $\mathbb {R} ^{3}$ 的一个子空间。证明向量集合 $U^{\perp }=\{{\vec {v}}\,{\big |}\,{\vec {v}}\cdot {\vec {u}}=0{\text{ for all }}{\vec {u}}\in U\}$ ，它与 $U$ 中的每个向量垂直也是 $\mathbb {R} ^{3}$ 的一个子空间。

解答

参考文献

Arrow, J. (1963), 社会选择与个人价值, Wiley.
Gardner, Martin (1970 年 4 月)，“数学游戏，太阳系中嵌入的一些数学奇事”，科学美国人：108-112.
Gardner, Martin (1974 年 10 月)，"数学游戏：从非传递关系中产生的悖论情况"，科学美国人.
Gardner, Martin (1980 年 10 月)，"数学游戏：从计票到让票数有效：选举的数学"，科学美国人.
Neimi, G.；Riker, W. (1976 年 6 月)，"投票制度的选择"，科学美国人：21–27.
Poundstone, W. (2008)，操纵选举，希尔与王，ISBN 978-0-8090-4893-9.
Taylor, Alan D. (1995)，数学与政治：策略、投票、权力和证明，施普林格出版社.
Zwicker, S. (1991)，"投票者悖论、旋转和博达计数"，数学社会科学，22：187–227

线性代数
← 主题：晶体	主题：投票悖论	主题：量纲分析 →