偏微分方程/泊松方程

本章讨论泊松方程

$\forall x\in \mathbb {R} ^{d}:-\Delta u(x)=f(x)$

假设 $f\in {\mathcal {C}}^{2}(\mathbb {R} ^{d})$，我们将通过分布理论证明一个解公式，并且对于满足一定性质边界条件的域，我们甚至可以证明边值问题的解公式。我们还会研究齐次泊松方程的解

$\forall x\in \mathbb {R} ^{d}:-\Delta u(x)=0$

齐次泊松方程的解称为调和函数。

多维积分的重要定理

在第 2 节中，我们看到了莱布尼茨积分法则，在第 4 节中，我们看到了富比尼定理。在本节中，我们将回顾多维积分中其他的一些定理，这些定理对于将分布理论应用于偏微分方程至关重要。不会给出证明，因为理解这些定理的证明对于理解本维基教科书并不重要。唯一例外是定理 6.3，它由定理 6.2 推导出。该定理的证明是一道习题。

定理 6.2:（散度定理）

令 $K\subset \mathbb {R} ^{d}$ 是一个具有光滑边界的紧集。如果 $\mathbf {V} :K\to \mathbb {R} ^{d}$ 是一个向量场，则

$\int _{K}\nabla \cdot \mathbf {V} (x)dx=\int _{\partial K}\nu (x)\cdot \mathbf {V} (x)dx$

, 其中 $\nu :\partial K\to \mathbb {R} ^{d}$ 是外法向量。

定理 6.3:（多维分部积分）

令 $K\subset \mathbb {R} ^{d}$ 是一个具有光滑边界的紧集。如果 $f:K\to \mathbb {R}$ 是一个函数，并且 $\mathbf {W} :K\to \mathbb {R} ^{d}$ 是一个向量场，则

$\int _{K}f(x)\nabla \cdot \mathbf {W} (x)dx=\int _{\partial K}f(x)\nu (x)\cdot \mathbf {W} (x)dx-\int _{K}\mathbf {W} (x)\cdot \nabla f(x)dx$

, 其中 $\nu :\partial K\to \mathbb {R} ^{d}$ 是外法向量。

证明: 见练习 1。

d 维球体的体积和表面积

定义 6.5:

Gamma 函数 $\Gamma :\mathbb {R} _{>0}\to \mathbb {R}$ 定义为

$\Gamma (x):=\int _{0}^{\infty }s^{x-1}e^{-s}ds$

Gamma 函数满足以下等式

定理 6.6:

$\forall x\in \mathbb {R} _{>0}:\Gamma (x+1)=x\Gamma (x)$

证明:

$\Gamma (x+1)=\int _{0}^{\infty }s^{x}e^{-s}ds{\overset {\text{integration by parts}}{=}}\underbrace {-s^{x}e^{-s}{\big |}_{s=0}^{s=\infty }} _{=0}-\int _{0}^{\infty }-xs^{x-1}e^{-s}ds=x\Gamma (x)$

$\Box$

如果 Gamma 函数向右平移 1 个单位，它就是阶乘函数的插值（见练习 2）

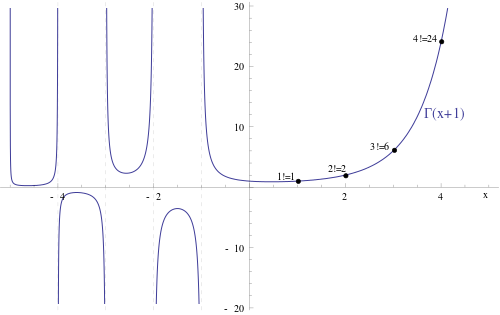
如上图所示，Gamma 函数在负数上也有值。 这是因为上图显示的是 Gamma 函数的一种自然延拓，这种延拓可以通过复分析来构造。

定义和定理 6.7:

$d$ 维球面坐标，由 $\Psi :(0,\infty )\times (0,2\pi )\times (-\pi /2,\pi /2)^{d-2}\to \mathbb {R} ^{d}\setminus \{(x_{1},\ldots ,x_{d})\in \mathbb {R} ^{d}:x_{1}\geq 0\wedge x_{2}=0\}$

$\Psi (r,\Phi ,\Theta _{1},\ldots ,\Theta _{d-2})={\begin{pmatrix}r\cos(\Phi )\cos(\Theta _{1})\cdots \cos(\Theta _{d-2})\\r\sin(\Phi )\cos(\Theta _{1})\cdots \cos(\Theta _{d-2})\\r\sin(\Theta _{1})\cos(\Theta _{2})\cdots \cos(\Theta _{d-2})\\\vdots \\r\sin(\Theta _{d-3})\cos(\Theta _{d-2})\\r\sin(\Theta _{d-2})\\\end{pmatrix}}$

是一个微分同胚。 的雅可比矩阵的行列式，$\Psi$, $\det J_{\Psi }$, 由下式给出

$\det J_{\Psi }(r,\Phi ,\Theta _{1},\ldots ,\Theta _{d-2})=r^{d-1}\cos(\Theta _{1})\cos(\Theta _{2})^{2}\cdots \cos(\Theta _{d-2})^{d-2}$

证明:

定理 6.8:

半径为 $R\in \mathbb {R} _{>0}$ 的 $d$ 维球体的体积，$B_{R}(0)$ 由下式给出

$V_{d}(R):={\frac {\pi ^{d/2}}{\Gamma (d/2+1)}}R^{d}$

证明:

定理 6.9:

半径为 $R\in \mathbb {R} _{>0}$ 的 $d$ 维球体的表面积（即 $\partial B_{R}(0)$ 的面积）由下式给出

$A_{d}(R):={\frac {d\pi ^{d/2}}{\Gamma (d/2+1)}}R^{d-1}$

半径为 $R\in \mathbb {R} _{>0}$ 的 $d$ 维球体的表面积和体积之间存在“微分关系”（见练习 3）。

证明:

${\begin{aligned}A_{d}(R)&:={\frac {d\pi ^{d/2}}{\Gamma (d/2+1)}}R^{d-1}&\\&={\frac {d}{R}}V_{d}(R)&\\&={\frac {d}{R}}\int _{B_{R}(0)}1dx&{\text{ theorem 6.8}}\\&=\int _{B_{R}(0)}{\frac {1}{R}}\nabla \cdot xdx&\\&=\int _{\partial B_{R}(0)}{\frac {1}{R}}{\frac {x}{R}}\cdot xdx&{\text{ divergence theorem}}\\&=\int _{\partial B_{R}(0)}1dx&\end{aligned}}$$\Box$

格林函数

我们回顾积分论中的一个事实

引理 6.11: $f$ 可积 $\Leftrightarrow$ $|f|$ 可积。

我们省略证明。

定理 6.12:

由下式给出的函数 $P:\mathbb {R} ^{d}\to \mathbb {R}$，

$P(x):={\begin{cases}-{\frac {1}{2}}|x|&d=1\\-{\frac {1}{2\pi }}\ln(\|x\|)&d=2\\{\frac {1}{(d-2)A_{d}(1)\|x\|^{d-2}}}&d\geq 3\end{cases}}$

是泊松方程的格林函数。

我们只证明了定理 $d\geq 2$ 的情况。对于 $d=1$，请参考练习 4。

证明:

1.

我们证明 $P$ 在局部可积。令 $K\subseteq \mathbb {R} ^{d}$ 为紧集。我们需要证明

$\int _{K}P(x)dx$

是一个实数，根据引理 6.11，这等价于

$\int _{K}|P(x)|dx$

是一个实数。在 $\mathbb {R} ^{d}$ 中，紧致等价于有界且闭合，因此我们可以选择一个 $R>0$，使得 $K\subset B_{R}(0)$。不失一般性，我们可以选择 $R>1$，因为如果发现选择的 $R$ 是 $\leq 1$，那么任何 $R>1$ 也都可以。然后我们有

$\int _{K}|P(x)|dx\leq \int _{B_{R}(0)}|P(x)|dx$

对于 $d=2$，${\begin{aligned}\int _{B_{R}(0)}|P(x)|dx&=\int _{B_{1}(0)}-{\frac {1}{2\pi }}\ln(\|x\|)dx+\int _{B_{R}(0)\setminus B_{1}(0)}{\frac {1}{2\pi }}\ln(\|x\|)dx&\\&=\int _{B_{1}(0)}-{\frac {1}{2\pi }}\ln(\|x\|)dx+\int _{B_{R}(0)}{\frac {1}{2\pi }}\ln(\|x\|)dx-\int _{B_{1}(0)}{\frac {1}{2\pi }}\ln(\|x\|)dx&\\&=\int _{0}^{1}-{\frac {r}{\pi }}\ln(r)dr+\int _{0}^{R}{\frac {r}{2\pi }}\ln(r)dr&{\text{int. by subst. using spherical coords.}}\\&={\frac {1}{4\pi }}+{\frac {R^{2}}{4\pi }}\left(\ln(R)-{\frac {1}{2}}R\right)<\infty \end{aligned}}$

对于 $d\geq 3$，

${\begin{aligned}\int _{B_{R}(0)}|P(x)|dx&=\int _{B_{R}(0)}{\frac {1}{(d-2)A_{d}(1)\|x\|^{d-2}}}\\&=\int _{0}^{R}\int _{0}^{2\pi }\underbrace {\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}\cdots \int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}} _{d-2{\text{ times}}}\overbrace {|r^{d-1}\cos(\Theta _{1})\cdots \cos(\Theta _{d-2})^{d-2}|} ^{\leq r^{d-1}}{\frac {1}{(d-2)A_{d}(1)r^{d-2}}}d\Theta _{1}\cdots d\Theta _{d-2}d\Phi dr\\&\leq \int _{0}^{R}2{\frac {r^{d-1}}{(d-2)A_{d}(1)r^{d-2}}}\pi ^{d-1}dr\\&={\frac {\pi ^{d-1}}{(d-2)A_{d}(1)}}R^{2}\end{aligned}}$

，其中我们将球坐标替换积分法应用于第一行到第二行。

2.

我们计算了一些$P$ 的导数（见练习 5）

对于$d=2$，我们有

$\forall x\in \mathbb {R} ^{d}\setminus \{0\}:\nabla P(x)=-{\frac {x}{2\pi \|x\|^{2}}}$

对于$d\geq 3$，我们有

$\forall x\in \mathbb {R} ^{d}\setminus \{0\}:\nabla P(x)={\frac {x}{A_{d}(1)\|x\|^{d}}}$

对于所有 $d\geq 2$，我们有 $\forall x\in \mathbb {R} ^{d}\setminus \{0\}:\Delta P(x)=0$

3.

我们证明

$\forall x\in \mathbb {R} ^{d}:-\Delta {\mathcal {T}}_{P(\cdot -x)}=\delta _{x}$

令 $x\in \mathbb {R} ^{d}$ 和 $\varphi \in {\mathcal {D}}(\mathbb {R} ^{d})$ 是任意的。在证明的最后一步中，我们只处理 $-\Delta {\mathcal {T}}_{P(\cdot -x)}(\varphi )$ 项。由于 $\varphi \in {\mathcal {D}}(\mathbb {R} ^{d})$，$\varphi$ 的支撑是紧的。我们定义

$K:={\text{supp }}\varphi \cup {\overline {B_{1}(x)}}$

由于

${\begin{aligned}-\Delta {\mathcal {T}}_{P(\cdot -x)}(\varphi )&={\mathcal {T}}_{P(\cdot -x)}(-\Delta \varphi )&\\&=\int _{\mathbb {R} ^{d}}P(y-x)(-\Delta \varphi (y))dy&\\&=\int _{K}P(y-x)(-\Delta \varphi (y))dy&\\&=\lim _{\epsilon \downarrow 0}\int _{K}P(y-x)(-\Delta \varphi (y))\chi _{K\setminus B_{\epsilon }(x)}(y)dy&{\text{dominated convergence}}\\&=\lim _{\epsilon \downarrow 0}\int _{K\setminus B_{\epsilon }(x)}P(y-x)(-\Delta \varphi (y))dy&\\\end{aligned}}$

, 其中 $\chi _{K\setminus B_{\epsilon }(0)}$ 是 $K\setminus B_{\epsilon }(0)$ 的特征函数。

最后一个积分是在 $K\setminus B_{\epsilon }(x)$ 上进行的（它是封闭集 $K$ 和 $\mathbb {R} ^{d}\setminus B_{\epsilon }(x)$ 的交集，因此也是有界的和紧致的）。在这个区域中，根据本证明的第二部分，$P(y-x)$ 是连续可微的。因此，我们可以用分部积分法。注意到 ${\frac {x-y}{\|y-x\|}}$ 是 $y\in \partial B_{\epsilon }(x)$ 在 $K\setminus B_{\epsilon }(x)$ 上的外法线向量，我们得到

$\int _{K\setminus B_{\epsilon }(x)}P(y-x)\overbrace {(-\Delta \varphi (y))} {=-\nabla \cdot \nabla \varphi (y)}dy=\int _{\partial B_{\epsilon }(x)}P(y-x)\nabla \varphi (y)\cdot {\frac {x-y}{\|y-x\|}}dy-\int _{\mathbb {R} ^{d}\setminus B_{\epsilon }(x)}\nabla \varphi (y)\cdot \nabla P(y-x)dy$

进一步选择 $w(x)={\tilde {G}}(x-\xi )\nabla \varphi (x)$。然后

$\nabla \cdot w(x)=\Delta \varphi (x){\tilde {G}}(x-\xi )+\langle \nabla {\tilde {G}}(x-\xi ),\nabla \varphi (x)\rangle$.

从高斯定理，我们得到

$\int _{\mathbb {R} ^{d}\setminus B_{R}(\xi )}\Delta \varphi (x){\tilde {G}}(x-\xi )+\langle \nabla {\tilde {G}}(x-\xi ),\nabla \varphi (x)\rangle dx=-\int _{\partial B_{R}(\xi )}\langle {\tilde {G}}(x-\xi )\nabla \varphi (x),{\frac {x-\xi }{\|x-\xi \|}}\rangle dx$

，其中右侧的减号是因为我们需要 *向内* 法向量。由此立即得出

$\int _{\mathbb {R} ^{d}\setminus B_{R}(\xi )}-\Delta \varphi (x){\tilde {G}}(x-\xi )=\underbrace {\int _{\partial B_{R}(\xi )}\langle {\tilde {G}}(x-\xi )\nabla \varphi (x),{\frac {x-\xi }{\|x-\xi \|}}\rangle dx} _{:=J_{1}(R)}-\underbrace {\int _{\mathbb {R} ^{d}\setminus B_{R}(\xi )}\langle \nabla {\tilde {G}}(x-\xi ),\nabla \varphi (x)\rangle dx} _{:=J_{2}(R)}$

我们现在可以使用柯西-施瓦茨不等式计算以下内容

$|J_{1}(R)|\leq \int _{\partial B_{R}(\xi )}\|{\tilde {G}}(x-\xi )\nabla \varphi (x)\|\overbrace {\|{\frac {x-\xi }{\|x-\xi \|}}\|} ^{=1}dx$

$={\begin{cases}\displaystyle \int _{\partial B_{R}(\xi )}-{\frac {1}{2\pi }}\ln |x-\xi |\|\nabla \varphi (x)\|dx=\int _{\partial B_{1}(\xi )}-R{\frac {1}{2\pi }}\ln \|R(x-\xi )\|\|\nabla \varphi (Rx)\|dx&d=2\\\displaystyle \int _{\partial B_{R}(\xi )}{\frac {1}{(d-2)c}}{\frac {1}{|x-\xi |^{d-2}}}\|\nabla \varphi (x)\|dx=\int _{\partial B_{1}(\xi )}R^{d-1}{\frac {1}{(d-2)c}}{\frac {1}{|R(x-\xi )|^{d-2}}}&d\geq 3\end{cases}}$

$\leq {\begin{cases}\displaystyle \max \limits _{x\in \mathbb {R} ^{d}}\|\nabla \varphi (Rx)\|\int _{\partial B_{1}(\xi )}-R{\frac {1}{2\pi }}\ln R^{2}dx=-\max \limits _{x\in \mathbb {R} ^{d}}\|\nabla \varphi (Rx)\|{\frac {c}{2\pi }}R\ln R^{2}\to 0,R\to 0&d=2\\\displaystyle \max \limits _{x\in \mathbb {R} ^{d}}\|\nabla \varphi (Rx)\|\int _{\partial B_{1}(\xi )}{\frac {1}{(d-2)c}}Rdx=\max \limits _{x\in \mathbb {R} ^{d}}\|\nabla \varphi (Rx)\|{\frac {R}{d-2}}\to 0,R\to 0&d\geq 3\end{cases}}$

现在我们定义 $v(x)=\varphi (x)\nabla {\tilde {G}}(x-\xi )$，这将得到

$\nabla \cdot v(x)=\varphi (x)\underbrace {\Delta {\tilde {G}}(x-\xi )} _{=0,x\neq \xi }+\langle \nabla \varphi (x),\nabla {\tilde {G}}(x-\xi )\rangle$

对 $v$ 应用高斯定理，得到

$J_{2}(R)=\int _{\partial B_{R}(\xi )}\varphi (x)\langle \nabla {\tilde {G}}(x-\xi ),{\frac {x-\xi }{\|x-\xi \|}}\rangle dx$

$=\int _{\partial B_{R}(\xi )}\varphi (x)\langle -{\frac {x-\xi }{c\|x-\xi \|^{d}}},{\frac {x-\xi }{\|x-\xi \|}}\rangle dx=-{\frac {1}{c}}\int _{\partial B_{R}(\xi )}{\frac {1}{R^{d-1}}}\varphi (x)dx$

，注意到 $d=2\Rightarrow c=2\pi$.

我们还注意到

$\varphi (\xi )={\frac {1}{c}}\int _{\partial B_{1}(\xi )}\varphi (\xi )dx={\frac {1}{c}}\int _{\partial B_{R}(\xi )}{\frac {1}{R^{d-1}}}\varphi (\xi )dx$

因此，我们有

$\lim _{R\to 0}|-J_{2}(R)-\varphi (\xi )|\leq {\frac {1}{c}}\lim _{R\to 0}\int _{\partial B_{R}(\xi )}{\frac {1}{R^{d-1}}}|\varphi (\xi )-\varphi (x)|dx\leq \lim _{R\to 0}{\frac {1}{c}}\max _{x\in B_{R}(\xi )}|\varphi (x)-\varphi (\xi )|\int _{\partial B_{1}(\xi )}1dx$

$=\lim _{R\to 0}\max _{x\in B_{R}(\xi )}|\varphi (x)-\varphi (\xi )|=0$

由于 $\varphi$ 的连续性。

因此，我们可以得出结论：

$\forall \Omega {\text{ domain of }}\mathbb {R} ^{d}:\forall \varphi \in {\mathcal {D}}(\Omega ):-\Delta T_{{\tilde {G}}(\cdot -\xi )}(\varphi )=\lim _{R\to 0}J_{0}(R)=\lim _{R\to 0}J_{1}(R)-J_{2}(R)=0+\varphi (\xi )=\delta _{\xi }(\varphi )$.

因此， ${\tilde {G}}$ 是 $d\geq 2$ 的泊松方程的格林函数。

证毕。

球面积分

定理 6.12:

设 $f:\mathbb {R} ^{d}\to \mathbb {R}$ 为一个函数。 $\int _{\partial B_{R}(0)}f(x)dx=R^{d-1}\int _{0}^{2\pi }\underbrace {\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}\cdots \int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}} _{d-2{\text{ times}}}f\left(\Psi (r,\Phi ,\Theta _{1},\ldots ,\Theta _{d-2})\right)\cos(\Theta _{1})\cos(\Theta _{2})^{2}\cdots \cos(\Theta _{d-2})^{d-2}d\Theta _{1}d\Theta _{2}\cdots d\Theta _{d-2}d\Phi$

证明：我们选择球面的边界方向作为方向。我们知道对于 $\partial B_{r}(0)$，一个外向法向量场由 $\nu (x)={\frac {x}{r}}$给出。作为 $B_{r}(0)$ 的参数化，我们只选择恒等函数，得到切空间的基是标准基，这反过来意味着 $B_{r}(0)$ 的体积形式为

$\omega _{B_{r}(0)}(x)=e_{1}^{*}\wedge \cdots \wedge e_{d}^{*}$

现在，我们使用法向量场来获得 $\partial B_{r}(0)$ 的体积形式

$\omega _{\partial B_{r}(0)}(x)(v_{1},\ldots ,v_{d-1})=\omega _{B_{r}(0)}(x)(\nu (x),v_{1},\ldots ,v_{d-1})$

我们将 $\omega _{B_{r}(0)}(x)$ 的公式代入，然后使用拉普拉斯行列式公式

$=e_{1}^{*}\wedge \cdots \wedge e_{d}^{*}(\nu (x),v_{1},\ldots ,v_{d-1})={\frac {1}{r}}\sum _{i=1}^{d}(-1)^{i+1}x_{i}e_{1}^{*}\cdots \wedge e_{i-1}^{*}\wedge e_{i+1}^{*}\wedge \cdots \wedge e_{d}^{*}(v_{1},\ldots ,v_{d-1})$

作为 $\partial B_{r}(x)$ 的参数化，我们选择半径为 $r$ 的球坐标。

我们计算球坐标的雅可比矩阵

$J=\left({\begin{smallmatrix}\cos(\varphi )\cos(\vartheta _{1})\cdots \cos(\vartheta _{d-2})&r-\sin(\varphi )\cos(\vartheta _{1})\cdots \cos(\vartheta _{d-2})&-r\cos(\varphi )\sin(\vartheta _{1})\cdots \cos(\vartheta _{d-2})&\cdots &\cdots &-r\cos(\varphi )\cos(\vartheta _{1})\cdots \sin(\vartheta _{d-2})\\\sin(\varphi )\cos(\vartheta _{1})\cdots \cos(\vartheta _{d-2})&r\cos(\varphi )\cos(\vartheta _{1})\cdots \cos(\vartheta _{d-2})&-r\sin(\varphi )\sin(\vartheta _{1})\cdots \cos(\vartheta _{d-2})&\cdots &\cdots &-r\sin(\varphi )\cos(\vartheta _{1})\cdots \sin(\vartheta _{d-2})\\\vdots &0&\ddots &\ddots &\ddots &\vdots \\\vdots &\vdots &\ddots &\ddots &\ddots &\\\sin(\vartheta _{d-3})\cos(\vartheta _{d-2})&0&\cdots &0&r\cos(\vartheta _{d-3})\cos(\vartheta _{d-2})&r\sin(\vartheta _{d-3})\cos(\vartheta _{d-2})\\\sin(\vartheta _{d-2})&0&\cdots &\cdots &0&r\cos(\vartheta _{d-2})\end{smallmatrix}}\right)$

我们观察到，在第一列中，我们只有球坐标除以 $r$。如果我们固定 $r$，则第一列消失。我们称得到的矩阵为 $J'$，我们的参数化，即球坐标，其中 $r$ 为常数，记为 $\Psi$。然后我们有

$\Psi ^{*}\omega _{\partial B_{r}(0)}(x)(v_{1},\ldots ,v_{d-1})=\omega _{\partial B_{r}(0)}(\Psi (x))(J'v_{1},\ldots ,J'v_{d-1})$

$={\frac {1}{r}}\sum _{i=1}^{d}(-1)^{i+1}\Psi (x)_{i}e_{1}^{*}\cdots \wedge e_{i-1}^{*}\wedge e_{i+1}^{*}\wedge \cdots \wedge e_{d}^{*}(J'v_{1},\ldots ,J'v_{d-1})$

$={\frac {1}{r}}\sum _{i=1}^{d}(-1)^{i+1}\Psi (x)_{i}\det(e_{j}^{*}(J'v_{k}))_{j\neq i}=\det J\cdot \det(v_{1},\ldots ,v_{d-1})$

回顾

$\det J=r^{d-1}\cos(\phi _{1})^{n-2}\cos(\phi _{2})^{d-3}\cdots \cos(\phi _{d-2})$

, 由表面积分的定义可知结论成立。

定理 6.13:

令 $f:\mathbb {R} ^{d}\to \mathbb {R}$ 为一个函数。那么

$\int _{\mathbb {R} ^{d}}f(x)dx=\int _{0}^{\infty }r^{d-1}\int _{\partial B_{1}(0)}f(rx)dxdr$

证明:

我们有 $r\Psi (1,\Phi ,\Theta _{1},\ldots ,\Theta _{d-2})=\Psi (r,\Phi ,\Theta _{1},\ldots ,\Theta _{d-2})$，其中 $\Psi$ 是球坐标。因此，利用换元积分法、Fubini 定理以及上面单位球面积分公式，可得

${\begin{aligned}\int _{\mathbb {R} ^{d}}f(x)dx&=\int _{(0,\infty )\times (0,2\pi )\times (-\pi /2,\pi /2)^{d-2}}f(\Psi (x))|\det J_{\Psi }(x)|dx\\&=\int _{0}^{\infty }\int _{0}^{2\pi }\underbrace {\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}\cdots \int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}} _{d-2{\text{ times}}}f(\Psi (r,\Phi ,\Theta _{1},\ldots ,\Theta _{d-2}))r^{d-1}\cos(\Theta _{1})\cdots \cos(\Theta _{d-2})^{d-2}d\Theta _{1}\cdots d\Theta _{d-2}d\Phi dr\\&=\int _{0}^{\infty }r^{d-1}\int _{0}^{2\pi }\underbrace {\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}\cdots \int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}} _{d-2{\text{ times}}}f(r\Psi (1,\Phi ,\Theta _{1},\ldots ,\Theta _{d-2}))\cos(\Theta _{1})\cdots \cos(\Theta _{d-2})^{d-2}d\Theta _{1}\cdots d\Theta _{d-2}d\Phi dr\\&=\int _{0}^{\infty }r^{d-1}\int _{\partial B_{1}(0)}f(rx)dr\end{aligned}}$$\Box$

调和函数

定义 6.14：设 $O\subseteq \mathbb {R} ^{d}$ 为开集，设 $u:O\to \mathbb {R}$ 为一个函数。如果 $u\in {\mathcal {C}}^{2}(O)$ 且

$\forall x\in O:\Delta u(x)=0$

$u$ 被称为**调和函数**。

定理 6.15:

设 $O\subseteq \mathbb {R} ^{d}$ 为开集，设 $u\in {\mathcal {C}}^{2}(O)$。以下条件等价

• $u$ 是调和的
• $\forall x\in O:\forall R{\text{ such that }}{\overline {B_{R}(0)}}\subset O:u(x)={\frac {1}{A_{d}(R)}}\int _{\partial B_{R}(x)}u(y)dy$
• $\forall x\in O:\forall R{\text{ such that }}{\overline {B_{R}(0)}}\subset O:u(x)={\frac {1}{V_{d}(R)}}\int _{B_{R}(x)}u(y)dy$

证明：我们定义以下函数

$\phi (r)={\frac {1}{r^{d-1}}}\int _{\partial B_{r}(x)}u(y)dy$

首先，通过微分同胚 $y\mapsto x+y$ 进行坐标变换，然后两次应用单位球面上的积分公式，我们得到

$\phi (r)={\frac {1}{r^{d-1}}}\int _{\partial B_{r}(0)}u(y+x)dy=\int _{\partial B_{1}(0)}u(x+ry)dy$

首先，对被积函数求导，然后使用高斯定理，我们知道

$\phi '(r)=\int _{\partial B_{1}(0)}\langle \nabla u(x+ry),y\rangle dy=\int _{B_{1}(0)}\Delta u(x+ry)dy=0$

情况 1： 如果 $u$ 是调和的，那么我们有

$\int _{B_{1}(0)}\Delta u(x+ry)dy=0$

，这就是 $\phi$ 为常数的原因。现在我们可以使用支配收敛定理进行以下计算

$\lim _{r\to 0}\phi (r)=\int _{\partial B_{1}(0)}\lim _{r\to 0}u(x+ry)dy=c(1)u(x)$

因此 $\phi (r)=c(1)u(x)$ 对于所有 $r$ 成立。

有了关系

$r^{d-1}c(1)=c(r)$

，这是因为我们对 $c(x),x\in \mathbb {R} _{>0}$ 的公式得出的，我们得到

$u(x)={\frac {\phi (r)}{c(1)}}={\frac {1}{c(1)}}{\frac {1}{r^{d-1}}}\int _{\partial B_{r}(x)}u(y)dy={\frac {1}{c(r)}}\int _{\partial B_{r}(x)}u(y)dy$

，这证明了第一个公式。

此外，我们可以通过首先进行变量变换，然后通过洋葱皮积分，然后使用该定理的第一个公式，最后再通过洋葱皮积分来证明第二个公式

$\int _{B_{r}(x)}u(y)dy=\int _{B_{r}(0)}u(y+x)dy=\int _{0}^{r}s^{d-1}\int _{\partial B_{1}(0)}u(y+sx)dxds=\int _{0}^{r}s^{d-1}u(x)\int _{\partial B_{1}(0)}1dxds=u(x)d(r)$

这表明如果 $u$ 是调和的，那么计算 $u$ 的两个公式都成立。

情况 2：假设 $u$ 不是调和函数。那么存在一个 $x\in \Omega$ 使得 $-\Delta u(x)\neq 0$。不失一般性，我们假设 $-\Delta u(x)>0$；对于 $-\Delta u(x)<0$ 的证明将完全类似，只是不等式的方向会互换。那么，由于如上所述，根据支配收敛定理，我们有

$\lim _{r\to 0}\phi '(r)=\int _{B_{1}(0)}\lim _{r\to 0}\Delta u(x+ry)dy>0$

由于 $\phi '$ 是连续的（根据支配收敛定理），因此 $\phi$ 在 $0$ 处增长，这与第一个公式矛盾。

与第二个公式的矛盾可以通过观察到 $\phi '$ 是连续的，因此存在一个 $\sigma \in \mathbb {R} _{>0}$

$\forall r\in [0,\sigma ):\phi '(r)>0$

这意味着，由于

$\lim _{r\to 0}\phi (r)=\int _{\partial B_{1}(0)}\lim _{r\to 0}u(x+ry)dy=c(1)u(x)$

因此

$\phi (0)=c(1)u(x)$

, 那么

$\forall r\in (0,\sigma ):\phi (r)>c(1)u(x)$

因此，通过与上面相同的计算，

$\int _{B_{r}(x)}u(y)dy=\int _{B_{r}(0)}u(y+x)dy=\int _{0}^{r}s^{d-1}\int _{\partial B_{1}(0)}u(y+sx)dxds>\int _{0}^{r}s^{d-1}u(x)\int _{\partial B_{1}(0)}1dxds=u(x)d(r)$

这表明（通过反证法证明）如果两个公式之一成立，则$u\in C^{2}(\Omega )$ 是调和的。

定义 6.16:

域 是 $\mathbb {R} ^{d}$ 的一个开连通子集。

为了证明下一个定理，我们需要来自其他学科的两个定理，第一个来自积分理论，第二个来自拓扑。

定理 6.17:

令 $B\subseteq \mathbb {R} ^{d}$ 且令 $f:B\to \mathbb {R}$ 是一个函数。如果

$\int _{B}|f(x)|dx=0$

则对于几乎所有 $x\in B$ 有 $f(x)=0$。

定理 6.18:

在一个连通拓扑空间中，唯一既开又闭的集合是整个空间和空集。

我们将省略证明。

定理 6.19:

令 $\Omega \subseteq \mathbb {R} ^{d}$ 是一个域，令 $u:\Omega \to \mathbb {R}$ 是调和的。如果存在一个 $x\in \Omega$ 使得

$u(x)=\sup _{y\in \Omega }u(y)$

, 则 $u$ 是常数。

证明:

我们选择

$B:=\left\{x\in \Omega :u(x)=\sup _{y\in \Omega }u(y)\right\}$

由于假设 $\Omega$ 是开集且 $B\subseteq \Omega$，对于每个 $x\in B$ 都存在一个 $R\in \mathbb {R} _{>0}$ 使得

${\overline {B_{R}(x)}}\subseteq \Omega$

根据定理 6.15，我们得到在这种情况下

$\sup _{y\in \Omega }u(y)=u(x)={\frac {1}{V_{d}(R)}}\int _{B_{R}(x)}u(z)dz$

此外，

$\sup _{y\in \Omega }u(y)=\sup _{y\in \Omega }u(y){\frac {V_{d}(R)}{V_{d}(R)}}={\frac {1}{V_{d}(R)}}\int _{B_{r}(x)}\sup _{y\in \Omega }u(y)dz$

，这就是为什么

${\begin{aligned}{\frac {1}{V_{d}(R)}}\int _{B_{R}(x)}u(z)dz=\int _{B_{R}(x)}\sup _{y\in \Omega }u(y)dz\\\Leftrightarrow {\frac {1}{V_{d}(R)}}\int _{B_{R}(x)}(u(z)-\sup _{y\in \Omega }u(y))dz=0\end{aligned}}$

由于

$\forall z\in \Omega :\sup _{y\in \Omega }u(y)\geq u(z)$

，我们甚至有

$0={\frac {1}{V_{d}(R)}}\int _{B_{R}(x)}(u(z)-\sup _{y\in \Omega }u(y))dz=-{\frac {1}{V_{d}(R)}}\int _{B_{R}(x)}|u(z)-\sup _{y\in \Omega }u(y)|dz$

根据定理 6.17，我们得出结论

$u(z)=\sup _{y\in \Omega }u(y)$

在 $B_{R}(x)$ 中几乎处处成立，并且由于

$z\mapsto u(z)-\sup _{y\in \Omega }u(y)$

是连续的，即使

$u(z)=\sup _{y\in \Omega }u(y)$

在 $B_{R}(x)$ 中处处成立（参见练习 6）。因此，$B_{R}(0)\subseteq B$，并且由于 $x\in B$ 是任意的，$B$ 是开集。

此外，

$B=u^{-1}\left(\left\{\sup _{y\in \Omega }u(y)\right\}\right)$

并且 $u$ 是连续的。因此，由于单点集是闭集，引理 3.13 指出 $B$ 在 $\Omega$ 中是闭集。因此 $B$ 既是开集又是闭集。根据定理 6.18，我们得到 $B=\emptyset$ 或 $B=\Omega$。由于假设 $B$ 非空，我们有 $B=\Omega$。$\Box$

定理 6.18:

令 $\Omega \subseteq \mathbb {R} ^{d}$ 是一个域，令 $u:\Omega \to \mathbb {R}$ 是调和的。如果存在一个 $x\in \Omega$ 使得

$u(x)=\inf _{y\in \Omega }u(y)$

, 则 $u$ 是常数。

证明：参见练习 7。

推论 6.20:

令 $\Omega \subseteq \mathbb {R} ^{d}$ 是一个有界区域，并令 $u:{\overline {\Omega }}\to \mathbb {R}$ 在 $\Omega$ 上是调和的，并且在 ${\overline {\Omega }}$ 上是连续的。那么

$\forall x\in {\overline {\Omega }}:\inf _{y\in \partial \Omega }u(y)\leq u(x)\leq \sup _{y\in \partial \Omega }u(y)$

证明:

定理 6.20:

令 $O\subseteq \mathbb {R} ^{d}$ 是一个开集，并且 $u:O\to \mathbb {R}$ 是一个调和函数，令 $x_{0}\in O$ 并且令 $R>0$ 使得 ${\overline {B_{R}(x_{0})}}\subset O$。那么

$\forall x\in B_{R}(x_{0}):u(x)={\frac {R^{2}+\|x-x_{0}\|^{2}}{RA_{d}(1)}}\int _{\partial B_{R}(x_{0})}{\frac {u(y)}{\|x-y\|^{d}}}dy$

证明:

接下来我们将证明每个调和函数 $u\in {\mathcal {C}}^{2}(O)$ 事实上自动包含在 ${\mathcal {C}}^{\infty }(O)$ 中。

定理 6.25：设 $O\subseteq \mathbb {R} ^{d}$ 是开集，并设 $u:O\to \mathbb {R}$ 是调和函数。则 $u\in {\mathcal {C}}^{\infty }(O)$。此外，对于所有 $n\in \mathbb {N}$，存在一个常数 $C_{d,n}$ 仅取决于维度 $d$ 和 $n$，使得对于所有 $x_{0}\in O$ 和 $R>0$ 使得 $B_{R}(x_{0})\subseteq O$

$\forall \alpha \in \mathbb {N} ^{d}{\text{ with }}|\alpha |=n:\partial _{\alpha }u(x)\leq {\frac {C_{d,n}}{R^{d+n}}}\int _{B_{R}(x_{0})}|u(y)|dy$

证明:

定义 6.26:

设 $(u_{l})_{l\in \mathbb {N} }$ 是调和函数序列，并设 $u:O\to \mathbb {R}$ 是一个函数。 $(u_{l})_{l\in \mathbb {N} }$ 局部一致收敛到 $u$ 当且仅当

定理 6.27:

设 $O\subseteq \mathbb {R} ^{d}$ 为开集，设 $u_{l}:O\to \mathbb {R} ,l\in \mathbb {N}$ 为调和函数，使得序列 $(u_{l})_{l\in \mathbb {N} }$ 局部一致收敛于函数 $u:O\to \mathbb {R}$。那么 $u$ 也是调和的。

证明:

定义 6.28:

定理 6.29: (阿泽拉-阿斯科利) 设 $F$ 是定义在紧集 $K$ 上的一组连续函数。那么以下两个命题等价

1. ${\overline {F}}$（$F$ 的闭包）是紧的
2. $F$ 是有界且等度连续的

证明:

定义 6.30:

定理 6.31:

设 $(u_{l})_{l\in \mathbb {N} }$ 是局部一致有界调和函数序列。那么它有一个局部一致收敛的子序列。

证明:

边界值问题

泊松方程的狄利克雷问题是寻找以下方程的解：

${\begin{cases}-\Delta u(x)=f(x)&x\in \Omega \\u(x)=g(x)&x\in \partial \Omega \end{cases}}$

解的唯一性

如果 $\Omega$ 是有界的，那么我们可以知道，如果问题

${\begin{cases}-\Delta u(x)=f(x)&x\in \Omega \\u(x)=g(x)&x\in \partial \Omega \end{cases}}$

有一个解 $u_{1}$，那么这个解在 $\Omega$ 上是唯一的。

证明：令 $u_{2}$ 为另一个解。如果我们定义 $u=u_{1}-u_{2}$，那么 $u$ 显然满足问题

${\begin{cases}-\Delta u(x)=0&,x\in \Omega \\u(x)=0&x\in \partial \Omega \end{cases}}$

，因为 $-\Delta (u_{1}(x)-u_{2}(x))=-\Delta u_{1}(x)-(-\Delta u_{2}(x))=f(x)-f(x)=0$ 对于 $x\in \Omega$，并且 $u_{1}(x)-u_{2}(x)=g(x)-g(x)=0$ 对于 $x\in \partial \Omega$。

根据以上最小值和最大值原理的推论，我们得到 $u$ 不仅在边界上恒为零，在整个域 $\Omega$ 上也是恒为零。因此 $u_{1}(x)-u_{2}(x)=0\Leftrightarrow u_{1}(x)=u_{2}(x)$ 在 $\Omega$ 上。这就是我们要证明的结论。

第一类格林函数

令 $\Omega \subseteq \mathbb {R} ^{d}$ 为一个域。令 ${\tilde {G}}$ 为泊松方程的格林核，我们已经在上文中计算了它，即

${\tilde {G}}(x):={\begin{cases}-{\frac {1}{2}}|x|&d=1\\-{\frac {1}{2\pi }}\ln \|x\|&d=2\\{\frac {1}{(d-2)c}}{\frac {1}{\|x\|^{d-2}}}&d\geq 3\end{cases}}$

, 其中 $c:=\int _{\partial B_{1}(0)}1dz$ 表示 $B_{1}(0)\subset \mathbb {R} ^{d}$ 的表面积。

假设存在一个函数 $h:\Omega \times \Omega \to \mathbb {R}$ 满足以下条件

${\begin{cases}-\Delta h(x,\xi )=0&x\in \Omega \\h(x,\xi )={\tilde {G}}(x-\xi )&x\in \partial \Omega \end{cases}}$

那么，$-\Delta$ 对 $\Omega$ 的**第一类格林函数**定义如下

${\tilde {G}}_{\Omega }(x,\xi ):={\tilde {G}}(x-\xi )-h(x,\xi )$

${\tilde {G}}(x-\xi )-h(x,\xi )$ 自然地成为了 $-\Delta$ 的格林函数。这可以通过与验证 ${\tilde {G}}$ 是格林核完全相同的方式进行验证。我们只需要知道 $h$ 在极限过程中没有作用，因为它是有界的。

这个函数的一个性质是它满足以下条件

${\begin{cases}-\Delta {\tilde {G}}_{\Omega }(x,\xi )=0&x\in \Omega \setminus \{\xi \}\\{\tilde {G}}_{\Omega }(x,\xi )=0&x\in \partial \Omega \end{cases}}$

这两个方程中的第二个方程从定义中可以明显看出，而第一个方程则可以从我们上面计算（在计算格林函数时）得到的结果推导出，即对于$x\neq 0$，有$\Delta {\tilde {G}}(x)=0$。

表示公式

设$\Omega \subseteq \mathbb {R} ^{d}$ 是一个区域，设$u\in C^{2}(\Omega )$ 是狄利克雷问题的解

${\begin{cases}-\Delta u(x)=f(x)&x\in \Omega \\u(x)=g(x)&x\in \partial \Omega \end{cases}}$

。那么$u$ 具有以下表示公式

$u(\xi )=\int _{\Omega }-\Delta u(y){\tilde {G}}_{\Omega }(y,\xi )dy-\int _{\partial \Omega }u(y)\nu (y)\nabla _{y}{\tilde {G}}_{\Omega }(y,\xi )dy$

，其中${\tilde {G}}_{\Omega }$ 是$\Omega$ 的第一类格林函数。

证明：令

$J(\epsilon ):=\int _{\Omega \setminus B_{\epsilon }(\xi )}-\Delta u(y){\tilde {G}}_{\Omega }(y,\xi )dy$

。根据支配收敛定理，我们有

$\lim _{\epsilon \to 0}J(\epsilon )=\int _{\Omega }-\Delta u(y){\tilde {G}}_{\Omega }(y,\xi )dy$

使用多维积分分部，可以得到

$J(\epsilon )=-\int _{\partial \Omega }\underbrace {{\tilde {G}}_{\Omega }(y,\xi )} _{=0}\langle \nabla u(y),\nu (y)\rangle dy+\int _{\partial B_{\epsilon }(\xi )}{\tilde {G}}_{\Omega }(y,\xi )\langle \nabla u(y),{\frac {y-\xi }{\|y-\xi \|}}\rangle dy+\int _{\Omega \setminus B_{\epsilon }(\xi )}\langle \nabla u(y),\nabla _{x}{\tilde {G}}_{\Omega }(y,\xi )\rangle dy$

$=\underbrace {\int _{\partial B_{\epsilon }(\xi )}{\tilde {G}}_{\Omega }(y,\xi )\langle \nabla u(y),{\frac {y-\xi }{\|y-\xi \|}}\rangle dy} _{:=J_{1}(\epsilon )}-\int _{\Omega \setminus B_{\epsilon }(\xi )}\Delta {\tilde {G}}_{\Omega }(y,\xi )u(y)dy$

$-\underbrace {\int _{\partial B_{\epsilon }(\xi )}u(y)\langle \nabla {\tilde {G}}_{\Omega }(y,\xi ),{\frac {y-\xi }{\|y-\xi \|}}\rangle dy} _{:=J_{2}(\epsilon )}-\int _{\partial \Omega }u(y)\langle \nabla {\tilde {G}}_{\Omega }(y,\xi ),\nu (y)\rangle dy$

当我们证明泊松方程的格林函数公式时，我们已经证明了

$\lim _{\epsilon \to 0}-J_{2}(\epsilon )=u(\xi )$ 和

$\lim _{\epsilon \to 0}J_{1}(\epsilon )=0$

验证这一点唯一需要的额外信息是$h\in C^{\infty }(\Omega )$，这就是它保持有界的原因，而${\tilde {G}}$ 当$\epsilon \to 0$ 时趋于无穷大，这就是$h$ 在极限过程中不起作用的原因。

这证明了公式。

球体上的调和函数：狄利克雷问题的一个特例

球体的第一类格林函数

让我们选择

$h(x,\xi )={\tilde {G}}\left({\frac {\|\xi \|}{r}}\left(x-{\frac {r^{2}}{\|\xi \|^{2}}}\xi \right)\right)$

那么

${\tilde {G}}_{B_{r}(x_{0})}(x,\xi ):={\tilde {G}}(x-\xi )-h(x-x_{0},\xi -x_{0})$

是$B_{r}(x_{0})$ 的第一类格林函数。

证明：因为$\xi -x_{0}\in B_{r}(0)\Rightarrow {\frac {r^{2}}{\|\xi -x_{0}\|^{2}}}(\xi -x_{0})\notin B_{r}(0)$，因此

$\forall x,\xi \in B_{r}(0):-\Delta _{x}h(x-x_{0},\xi -x_{0})=0$

此外，我们得到

$\int _{B_{r}(x_{0})}-\Delta \varphi (x){\tilde {G}}_{\Omega }(x,\xi )dx=\int _{B_{r}(x_{0})}-\Delta \varphi (x){\tilde {G}}(x-\xi )dx+\int _{B_{r}(x_{0})}\varphi (x)-\Delta h(x,\xi )dx=\varphi (\xi )+0$

，这就是${\tilde {G}}_{\Omega }(x,\xi )$ 是格林函数的原因。

边界的性质来自以下计算

$\forall x\in \partial B_{r}(0):\|x-\xi \|^{2}=\langle x-\xi ,x-\xi \rangle =r^{2}+\|\xi \|^{2}-2\langle x,\xi \rangle ={\frac {\|\xi \|^{2}}{r^{2}}}(\langle x-{\frac {r^{2}}{\|\xi \|^{2}}}\xi ,x-{\frac {r^{2}}{\|\xi \|^{2}}}\xi \rangle )={\frac {\|\xi \|^{2}}{r^{2}}}\|x-{\frac {r^{2}}{\|\xi \|^{2}}}\xi \|^{2}$

因此，$x\in \partial B_{r}(0)\Rightarrow h(x,\xi )={\tilde {G}}(x,\xi )$，因为 ${\tilde {G}}$ 是径向对称的。

解的公式

让我们考虑以下问题

${\begin{cases}-\Delta u(x)=0&x\in B_{r}(0)\\u(x)=\varphi (x)&x\in \partial B_{r}(0)\end{cases}}$

这里 $\varphi$ 应该在 $\partial B_{r}(0)$ 上是连续的。 那么以下结论成立：该问题的唯一解 $u\in C({\overline {B_{r}(0)}})\cap C^{2}(B_{r}(0))$ 由以下给出：

$u(\xi )={\begin{cases}\int _{\partial B_{r}(0)}\langle -\nu (y),\nabla _{y}{\tilde {G}}_{B_{r}(0)}(y,\xi )\rangle \varphi (y)dy&\xi \in B_{r}(0)\\\varphi (\xi )&\xi \in \partial B_{r}(0)\end{cases}}$

证明：唯一性我们已经证明了；我们已经证明了对于所有 $-\Delta$ 在有界域上的狄利克雷问题（单位球当然是有界的），解是唯一的。

因此，剩下的就是证明上述函数是问题的解。为此，我们首先注意到

$-\Delta \int _{\partial B_{r}(0)}\langle -\nu (y),{\tilde {\nabla }}_{y}G_{B_{r}(0)}(y,\xi )\rangle \varphi (y)dy=-\Delta \int _{\partial B_{r}(0)}\langle -\nu (y),\nabla _{y}({\tilde {G}}(y-\xi )-h(y,\xi ))\rangle \varphi (y)dy$

令 $0<s<r$ 为任意值。由于 ${\tilde {G}}_{B_{r}(0)}$ 在 $B_{s}(0)$ 上是连续的，我们有，在 $B_{s}(0)$ 上它是 有界的。因此，根据基本估计，我们知道积分是有界的，因为球面（积分的集合）是一个有界集合，因此整个积分必须始终低于某个常数。但这意味着，我们允许在 $B_{s}(0)$ 上对积分进行微分，由于 $r>s>0$ 是任意的，我们可以直接得出结论，在 $B_{r}(0)$ 上，

$-\Delta u(\xi )=\int _{\partial B_{r}(0)}\overbrace {-\Delta (\langle -\nu (y),{\tilde {\nabla }}_{y}{\tilde {G}}(x-\xi )-h(x,\xi )\rangle \varphi (y))} ^{=0}dy=0$

此外，我们必须证明 $\forall x\in \partial B_{r}(0):\lim _{y\to x}u(y)=\varphi (x)$，即 $u$ 在边界上是连续的。

为此，我们首先注意到

$\int _{\partial B_{r}(0)}\langle -\nu (y),\nabla _{y}{\tilde {G}}_{B_{r}(0)}(y,\xi )\rangle dy=1$

这是因为，如果 $u\equiv 1$，那么 $u$ 是以下问题的解

${\begin{cases}-\Delta u(x)=0&x\in B_{r}(0)\\u(x)=1&x\in \partial B_{r}(0)\end{cases}}$

并应用表示公式。

此外，如果 $\|x-x^{*}\|<{\frac {1}{2}}\delta$ 并且 $\|y-x^{*}\|\geq \delta$，根据三角不等式，我们有

$\|x-y\|\geq |\|y-x^{*}\|-\|x^{*}-x\||\geq {\frac {1}{2}}\delta$

此外，根据三角不等式，我们还可以得到

$(r^{2}-\|x\|^{2})=(r+\|x\|)(r-\|x\|)=(r+\|x\|)(\|x^{*}\|-\|x\|)\leq 2r\|x^{*}-x\|$

令 $\epsilon >0$ 为任意值，并令 $x^{*}\in \partial B_{r}(0)$。 然后，根据 $\varphi$ 的连续性，我们可以选择 $\delta >0$ 使得

$\|x-x^{*}\|<\delta \Rightarrow |\varphi (x)-\varphi (x^{*})|<{\frac {\epsilon }{2}}$.

最后，借助我们之前做出的所有估计，我们可以展示最后一个不等式链，证明表示公式是正确的。

$|u(x)-u(x^{*})|=|u(x)-1\cdot \varphi (x^{*})|=\left|\int _{\partial B_{r}(0)}\langle -\nu (y),\nabla _{y}{\tilde {G}}_{B_{r}(0)}(y,x)\rangle (\varphi (x)-\varphi (x^{*}))dy\right|$

$\leq {\frac {\epsilon }{2}}\int _{\partial B_{r}(0)\cap B_{\delta }(x^{*})}|\langle -\nu (y),\nabla _{y}{\tilde {G}}_{B_{r}(0)}(y,x)\rangle |dy+2\|\varphi \|_{\infty }\int _{\partial B_{r}(0)\setminus B_{\delta }(x^{*})}|\langle -\nu (y),\nabla _{y}{\tilde {G}}_{B_{r}(0)}(y,x)\rangle |dy$

$\leq {\frac {\epsilon }{2}}+2\|\varphi \|_{\infty }\int _{\partial B_{r}(0)\setminus B_{\delta }(x^{*})}{\frac {r^{2}-\|x\|^{2}}{rc(1)\left({\frac {\delta }{2}}\right)^{d}}}dy\leq {\frac {\epsilon }{2}}+2\|\varphi \|_{\infty }r^{d-2}{\frac {r^{2}-\|x\|^{2}}{\left({\frac {\delta }{2}}\right)^{d}}}$

由于 $x\to x^{*}$ 意味着 $r^{2}-\|x\|^{2}\to 0$，我们可以选择 $x$ 足够接近 $x^{*}$ 使得

$2\|\varphi \|_{\infty }r^{d-2}{\frac {r^{2}-\|x\|^{2}}{\left({\frac {\delta }{2}}\right)^{d}}}<{\frac {\epsilon }{2}}$。由于$\epsilon >0$是任意的，这完成了证明。

障碍

设$\Omega \subset \mathbb {R} ^{d}$是一个域。函数$b:\mathbb {R} ^{d}\to \mathbb {R}$被称为关于$y\in \partial \Omega$的障碍 当且仅当满足以下性质

1. $b$是连续的
2. $b$在$\Omega$上是超调和的
3. $b(y)=0$
4. $\forall x\in \mathbb {R} ^{d}\setminus \Omega :b(x)>0$

外球条件

令 $\Omega \subseteq \mathbb {R} ^{d}$ 为一个区域。当且仅当对于所有的 $x\in \partial \Omega$ 都存在一个球 $B_{r}(z)\subseteq \mathbb {R} ^{d}\setminus \Omega$ 使得 $x\in \partial B_{r}(z)$，其中 $z\in \mathbb {R} ^{d}\setminus \Omega$ 和 $r\in \mathbb {R} _{\geq 0}$，则称它满足外球条件。

次调和函数和超调和函数

令 $\Omega \subseteq \mathbb {R} ^{d}$ 为一个区域，且 $v\in C(\Omega )$。

我们称 $v$ 为次调和函数，当且仅当

$v(x)\leq {\frac {1}{d(r)}}\int _{B_{r}(x)}v(y)dy$

我们称 $v$ 为超调和函数，当且仅当

$v(x)\geq {\frac {1}{d(r)}}\int _{B_{r}(x)}v(y)dy$

从这个定义我们可以看出，一个函数是调和函数当且仅当它既是次调和函数又是超调和函数。

超调和函数的最小值原理

在 $\Omega$ 上的超调和函数 $u$ 在 $\Omega$ 的边界 $\partial \Omega$ 上取得其最小值。

证明：与调和函数的最小值和最大值原理的证明几乎相同。作为一个练习，你可以尝试自己证明这个最小值原理。

调和降低

设 $u\in {\mathcal {S}}_{\varphi }(\Omega )$，设 $B_{r}(x_{0})\subset \Omega$。如果我们定义

${\tilde {u}}(x)={\begin{cases}u(x)&x\notin B_{r}(x_{0})\\\int _{\partial B_{r}(0)}\langle -\nu (y),\nabla _{y}{\tilde {G}}_{B_{r}(0)}(y,x)\rangle \varphi (y)dy&x\in B_{r}(x_{0})\end{cases}}$

，那么 ${\tilde {u}}\in {\mathcal {S}}_{\varphi }(\Omega )$。

证明：在这个证明中，需要注意的是 ${\tilde {u}}$ 在 $B_{r}(x_{0})$ 内部的公式不过是球上狄利克雷问题的解公式。因此，我们立即得到 ${\tilde {u}}$ 是超调和的，而且，在 $\partial \Omega$ 上的值不会改变，这就是为什么 ${\tilde {u}}\in {\mathcal {S}}_{\varphi }(\Omega )$。这正是要证明的。

定义 3.1

设 $\varphi \in C(\partial \Omega )$。然后我们定义以下集合

${\mathcal {S}}_{\varphi }(\Omega ):=\{u\in C({\overline {\Omega }}):u{\text{ superharmonic and }}x\in \partial \Omega \Rightarrow u(x)\geq \varphi (x)\}$

引理 3.2

${\mathcal {S}}_{\varphi }(\Omega )$ 不为空，并且

$\forall u\in {\mathcal {S}}_{\varphi }(\Omega ):\forall x\in \Omega :u(x)\geq \min _{y\in \partial \Omega }\varphi (y)$

证明：第一部分可以通过选择常数函数 $u(x)=\max _{y\in \partial \Omega }\varphi (y)$ 得出，该函数是调和的，因此是超调和的。第二部分从超调和函数的最小值原理得出。

引理 3.3

令 $u_{1},u_{2}\in {\mathcal {S}}_{\varphi }(\Omega )$。如果我们现在定义 $u(x)=\min\{u_{1}(x),u_{2}(x)\}$，则 $u\in {\mathcal {S}}_{\varphi }(\Omega )$。

证明：边界上的条件得到满足，因为

$\forall x\in \partial \Omega :u_{1}(x)\geq \varphi (x)\wedge u_{2}(x)\geq \varphi (x)$

$u$ 是超调和的，因为，如果我们（不失一般性）假设 $u(x)=u_{1}(x)$，则可以得出

$u(x)=u_{1}(x)\geq {\frac {1}{d(r)}}\int _{B_{r}(x)}u_{1}(y)dy\geq {\frac {1}{d(r)}}\int _{B_{r}(x)}u(y)dy$

，由于积分的单调性。这个论点对所有 $x\in \Omega$ 都有效，因此 $u$ 是超调和的。

引理 3.4

如果 $\Omega \subset \mathbb {R} ^{d}$ 是有界的，并且 $\varphi \in C(\partial \Omega )$，则函数

$u(x)=\inf\{v(x)|v\in {\mathcal {S}}_{\varphi }(\Omega )\}$

是调和的。

证明:

引理 3.5

如果 $\Omega$ 满足外球条件，则对于所有 $y\in \partial \Omega$ 都存在一个势垒函数。

佩龙存在定理

设 $\Omega \subset \mathbb {R} ^{d}$ 是一个满足外球条件的有界域。则泊松方程的狄利克雷问题，即再次写为

${\begin{cases}-\Delta u(x)=f(x)&x\in \Omega \\u(x)=g(x)&x\in \partial \Omega \end{cases}}$

有一个解 $u\in C^{\infty }(\Omega )\cap C({\overline {\Omega }})$。

证明:

让我们总结一下本节的结果。

推论 6.last:

设 $\Omega \subset \mathbb {R} ^{d}$ 是一个满足外球条件的域，设 $f\in {\mathcal {C}}^{2}(\mathbb {R} ^{d})$，设 $g:\partial \Omega \to \mathbb {R}$ 是连续的，并且设 $P_{\Omega }$ 是 $\Omega$ 的第一类格林函数。则

$u(x)=\int _{\Omega }f(y)P_{\Omega }(y,x)dy-\int _{\partial \Omega }g(y)\nu (y)\cdot \nabla _{y}P_{\Omega }(y,x)dy$

是边值问题的唯一连续解

${\begin{cases}\forall x\in \Omega :&-\Delta u(x)=f(x)\\\forall x\in \partial \Omega :&u(x)=g(x)\end{cases}}$

在下一章中，我们将研究热方程。

练习

1. 使用定理 6.2 证明定理 6.3（提示：在定理 6.2 中选择 $\mathbf {V} (x)=\mathbf {W} (x)f(x)$）。
2. 证明 $\forall n\in \mathbb {N} :\Gamma (n+1)=n!$，其中 $n!$ 是 $n$ 的阶乘。
3. 计算 $V_{d}'(R)$。你以前见过这个函数吗？
4. 证明对于 $d=1$，在定理 6.11 中定义的函数 $P_{d}$ 是泊松方程的格林函数（提示：使用分部积分两次）。
5. 对于所有 $d\geq 2$ 和 $x\in \mathbb {R} ^{d}\setminus \{0\}$，计算 $\nabla P_{d}(x)$ 和 $\Delta P_{d}(x)$。
6. 设 $O\subseteq \mathbb {R} ^{d}$ 为开集，且 $f:O\to \mathbb {R} ^{d}$ 为连续函数。证明 $f(x)=0$ 在 $O$ 中几乎处处成立，则意味着 $f(x)=0$ 在 $O$ 中处处成立。
7. 通过对定理 6.19 的证明进行模仿，证明定理 6.20。
8. 对于所有维度$d\geq 2$，给出向量$\alpha ,\beta \in \mathbb {N} _{0}^{d}$ 的一个例子，使得既不满足$\alpha \leq \beta$ 也不满足$\beta \leq \alpha$。