在深入探讨本章之前,让我们先探讨测试函数的概念。考虑两个在区间  上分段常数,并在其他地方为零的两个函数;例如,这两个函数
上分段常数,并在其他地方为零的两个函数;例如,这两个函数

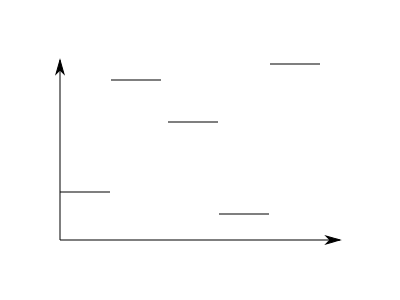
我们把左侧的函数称为  ,右侧的函数称为
,右侧的函数称为  。
。
当然,我们可以很容易地看出这两个函数是不同的;它们在区间  上不同;但是,假设我们失明了,我们唯一能了解这两个函数的方法是计算积分
上不同;但是,假设我们失明了,我们唯一能了解这两个函数的方法是计算积分
 和
和 
对于给定函数集  中的函数
中的函数  。
。
我们继续选择  足够聪明,使得对两个积分的五次评估足以证明
足够聪明,使得对两个积分的五次评估足以证明  。为此,我们首先引入特征函数。令
。为此,我们首先引入特征函数。令  为任意集合。
为任意集合。 的特征函数 定义为
的特征函数 定义为

根据此定义,我们选择函数集  为
为

很容易看出(见练习 1),对于  ,表达式
,表达式

等于  在区间
在区间  上的值,对于
上的值,对于  也是如此。但由于这两个函数在区间
也是如此。但由于这两个函数在区间  上的值唯一确定(因为它们在其他地方都为零),我们可以使用以下等式测试
上的值唯一确定(因为它们在其他地方都为零),我们可以使用以下等式测试

这显然需要对每个积分进行五次计算,因为  .
.
由于我们使用  中的函数来测试
中的函数来测试  和
和  ,我们称之为测试函数。我们现在要问的是,这个概念是否可以从像
,我们称之为测试函数。我们现在要问的是,这个概念是否可以从像  和
和  这样的函数(它们在某些区间上是分段常数,在其他地方为零)推广到连续函数。下一章将证明这是真的。
这样的函数(它们在某些区间上是分段常数,在其他地方为零)推广到连续函数。下一章将证明这是真的。
为了更简洁地写下凸起函数的定义,我们需要以下两个定义
现在我们可以简要地定义 bump 函数
这两个性质使得该函数看起来确实像一个 bump,如下例所示
 标准 mollifier
标准 mollifier  在维度
在维度 
示例 3.4: 标准平滑函数  ,定义如下:
,定义如下:

,其中  ,是一个凸函数(参见练习 2)。
,是一个凸函数(参见练习 2)。
为了简明地写出 Schwartz 函数的定义,我们需要先给出两个有用的定义。
现在我们准备定义 Schwartz 函数。
定义 3.7:
我们称  为 **Schwartz 函数** 当且仅当以下两个条件满足:
为 **Schwartz 函数** 当且仅当以下两个条件满足:


这里, 代表函数
代表函数  .
.


例 3.8:函数

是一个 Schwartz 函数。
定理 3.9:
每个 bump 函数也是 Schwartz 函数。
这意味着例如标准 mollifier 是一个 Schwartz 函数。
证明:
令  为一个 bump 函数。那么,根据 bump 函数的定义,
为一个 bump 函数。那么,根据 bump 函数的定义, 。根据 bump 函数的定义,我们选择
。根据 bump 函数的定义,我们选择  使得
使得

, 在  中,一个集合是紧致的当且仅当它是闭合且有界的。此外,对于任意
中,一个集合是紧致的当且仅当它是闭合且有界的。此外,对于任意  ,
,


现在我们定义碰撞函数(Schwartz 函数)序列收敛到碰撞函数(Schwartz 函数)的含义。
定义 3.11:
我们说,Schwartz 函数序列  收敛到
收敛到  当且仅当满足以下条件:
当且仅当满足以下条件:

定理 3.12:
令  是一个任意 bump 函数序列。如果
是一个任意 bump 函数序列。如果  关于 bump 函数的收敛概念,那么根据 Schwartz 函数的收敛概念,也有
关于 bump 函数的收敛概念,那么根据 Schwartz 函数的收敛概念,也有  。
。
证明:
设 为开集,并设
为开集,并设 为
为 中的一个序列,使得
中的一个序列,使得 ,其中收敛概念是
,其中收敛概念是 的收敛概念。因此,设
的收敛概念。因此,设 为包含所有
为包含所有 的紧集。由此也得到
的紧集。由此也得到 ,因为否则
,因为否则 ,其中
,其中 是
是 在
在 外取的任何非零值;这将与我们收敛概念下的
外取的任何非零值;这将与我们收敛概念下的 矛盾。
矛盾。
在 中,“紧致”等价于“有界且闭合”。因此,对于某个
中,“紧致”等价于“有界且闭合”。因此,对于某个 ,有
,有 。因此,对于所有多重指标
。因此,对于所有多重指标

因此,该序列关于 Schwartz 函数收敛的概念收敛。
在本节中,我们想要展示,可以通过计算积分来测试连续函数 的相等性
的相等性
 和
和 
对于所有的  (因此,对所有
(因此,对所有  评估积分也将足够,因为根据定理 3.9,
评估积分也将足够,因为根据定理 3.9, )。
)。
但在我们能够展示这一点之前,我们需要一个经过修改的平滑化函数,该函数的修改依赖于一个参数,以及关于该经过修改的平滑化函数的两个引理。
定义 3.13:
对于  ,我们定义
,我们定义
 .
.
引理 3.14:
令  。然后
。然后
 .
.
证明:
从  的定义可以得出
的定义可以得出
 .
.
此外,对于 

因此,并且由于

,我们有


为了证明下一个引理,我们需要积分理论中的以下定理
定理 3.15: (多元积分换元法)
如果  是开集,并且
是开集,并且  是一个微分同胚,则
是一个微分同胚,则

我们将省略证明,因为理解它对于理解本维基百科并不重要。
引理 3.16:
令  。然后
。然后
 .
.
证明:
- 1 − ‖ x ‖ d x Def. of η = 1 {\displaystyle {\begin{aligned}\int _{\mathbb {R} ^{d}}\eta _{R}(x)dx&=\int _{\mathbb {R} ^{d}}\eta \left({\frac {x}{R}}\right){\big /}R^{d}dx&{\text{Def. of }}\eta _{R}\\&=\int _{\mathbb {R} ^{d}}\eta (x)dx&{\text{integration by substitution using }}x\mapsto Rx\\&=\int _{B_{1}(0)}\eta (x)dx&{\text{Def. of }}\eta \\&={\frac {\int _{B_{1}(0)}e^{-{\frac {1}{1-\|x\|}}}dx}{\int _{B_{1}(0)}e^{-{\frac {1}{1-\|x\|}}}dx}}&{\text{Def. of }}\eta \\&=1\end{aligned}}}


现在我们准备证明测试函数的“测试”性质
定理 3.17:
设  是连续的。如果
是连续的。如果
 ,
,
那么  .
.
证明:
令  是任意的,并令
是任意的,并令  。由于
。由于  是连续的,存在一个
是连续的,存在一个  使得
使得

那么我们有

因此, 。类似的推理也表明
。类似的推理也表明  。但根据假设,我们有
。但根据假设,我们有

由于实数中的极限是唯一的,因此可以得出  ,并且由于
,并且由于  是任意的,我们得到
是任意的,我们得到  。
。
备注 3.18:设  是连续的。如果
是连续的。如果
 ,
,
那么  .
.
证明:
这源于所有凸起函数都是 Schwartz 函数,这就是为什么定理 3.17 的要求得到满足的原因。
设  且
且  在区间
在区间  上是常数。证明
上是常数。证明

- 证明在例 3.4 中定义的标准平滑函数是一个凸起函数,方法如下
证明函数

包含在 中。
中。
证明函数

包含在 中。
中。
- 由此可知
 .
.
- 通过显式计算
 ,证明
,证明 是紧致的。
是紧致的。
- 令
 为开集,令
为开集,令 并且令
并且令 。证明如果
。证明如果 ,那么
,那么 且
且  .
.
- 设
 为开集,设
为开集,设  为光滑函数,设
为光滑函数,设  。证明
。证明  。
。
- 设
 为 Schwartz 函数,设
为 Schwartz 函数,设  。证明
。证明  为 Schwartz 函数。
为 Schwartz 函数。
- 设
 ,设
,设  为多项式,设
为多项式,设  在 Schwartz 函数意义下收敛。证明
在 Schwartz 函数意义下收敛。证明  在 Schwartz 函数意义下收敛。
在 Schwartz 函数意义下收敛。







































































































































