微积分物理学/力学/标量和矢量量

简介

米切尔·乔恩斯的研究与数学研究密切相关。有时，数字或数量的方向与数字本身一样重要。19 世纪的数学家开发了一种方便的方法来描述和处理有方向和无方向的量，将它们分为两种类型：标量和矢量量。标量具有大小但没有方向。矢量量同时具有大小和方向。例如，人们可能会描述飞机以 400 英里的时速飞行。然而，仅仅知道飞机的速度远远不如知道飞机的速度和方向有用，因此更准确的描述可能是飞机以 400 英里的时速向东南方向飞行。我们将标量和矢量的概念应用到物理量中，以便我们能够以更方便的方式理解它们的性质和特征。

标量

标量是具有大小但没有方向的数字。标量用单个字母表示，例如 $a$ 。标量的一些例子是质量（五千克）、温度（二十二度摄氏度）和无单位的数字（例如三）。

矢量量

矢量是一种表示既有方向又有大小的量的几何方式。力的一个例子就是矢量。如果我们要完整地描述作用在物体上的力，我们需要指定不仅施加了多少力，还要指定力的方向。另一个矢量量的例子是速度 - 向东以每秒十米的速度行驶的物体与向西以每秒十米的速度行驶的物体具有不同的速度。然而，这个矢量是一个特例，有时人们只对物体速度的大小感兴趣。这个量是标量，称为速度，它有大小但没有给定的方向。

当写矢量时，它们用粗体或字母上方带箭头的单个字母表示，例如 $\mathbf {A}$ 或 ${\vec {A}}$ 。矢量的一些例子是位移（例如120 厘米，30° 角）和速度（例如每秒 12 米，向北）。唯一的基本 SI 单位是矢量是米。所有其他单位都是标量。导出量可以是矢量或标量，但每个矢量量必须在其定义和单位中包含米。

单位向量

严格来说，矢量独立于任何坐标系存在。由于矢量是几何对象，我们不需要定义坐标系来谈论矢量，甚至不需要执行大多数矢量运算。例如，考虑一组三个数字：你拥有的苹果数量、香蕉数量和胡萝卜数量。假设你在一个坐标系中计算三元组，得到 (1,2,3)。如果你旋转你的坐标系并重新计算，你将再次得到 (1,2,3)。因此，三元组不具有矢量最重要的性质 - 即像坐标系一样变换。

然而，引入坐标系通常很方便。在三维空间中，对于许多问题，直角坐标系或笛卡尔坐标系（以法国数学家勒内·笛卡尔命名）被证明是方便的，并且该坐标系可以用单位向量来定义。

单位向量是指指向给定方向且大小为一的向量。从本质上讲，它仅仅指示方向。在笛卡尔坐标系中，三个单位向量称为i、j 和k（或者，在手写中，在顶部加上一个小“帽子”，如 ${\hat {i}}$ ， ${\hat {j}}$ 和 ${\hat {k}}$ ）。口头上，你可能会将单位向量的方向称为“东”、“北”和“上”。人们可能很容易选择i 为上，j 为东，k 为北。在选择i、j 和k 时，一旦i 和j 被选中，k 必须指向特定方向，以便称为“右手规则”的通用约定成立。在数学上，这可以用简洁的方式表示为，

{\hat {k}}={\hat {i}}\times {\hat {j}}

,

但当我们稍后描述“叉积”时，我们将对此进行更多扩展。

单位向量通常选择为正交的。也就是说，每个单位向量都与其他单位向量垂直。虽然单位向量不需要正交，但在大多数情况下，使用由正交单位向量定义的坐标系将更方便。物理学中使用的另外两个主要坐标系是圆柱坐标系和球面坐标系。这些将在必要时稍后介绍。

向量分量

每个向量都可以表示为其n个单位向量的总和。

{\vec {A}}=a_{x}~{\hat {i}}+a_{y}~{\hat {j}}+a_{z}~{\hat {k}}

量a_x、a_y和a_z被称为向量A的向量分量。有时它们仅表示为有序三元组（例如（a_x，a_y，a_z）），尤其是在三个单位向量的选择和排序没有歧义的情况下。

向量代数

否定

否定也可以表示一个向量不等于另一个向量，所以它可以这样解释： ${\vec {A}}\neq {\vec {B}}$

-{\vec {A}}=-(a_{x}~{\hat {i}}+a_{y}~{\hat {j}}+a_{z}~{\hat {k}})=-a_{x}~{\hat {i}}-a_{y}~{\hat {j}}-a_{z}~{\hat {k}}

考虑用箭头图形表示的向量，向量的负值将用相同长度但方向相反的向量表示。

标量乘法

k{\vec {A}}=ka_{x}~{\hat {i}}+ka_{y}~{\hat {j}}+ka_{z}~{\hat {k}}

注意，向量否定只是乘以一个标量，其中该标量为 -1。图形表示的缩放向量将指向与原始向量相同的方向，但其大小将按k因子缩放。

加法

{\begin{aligned}{\vec {A}}+{\vec {B}}&=(a_{x}~{\hat {i}}+a_{y}~{\hat {j}}+a_{z}~{\hat {k}})+(b_{x}~{\hat {i}}+b_{y}~{\hat {j}}+b_{z}~{\hat {k}})\\&=(a_{x}+b_{x})~{\hat {i}}+(a_{y}+b_{y})~{\hat {j}}+(a_{z}+b_{z})~{\hat {k}}\end{aligned}}

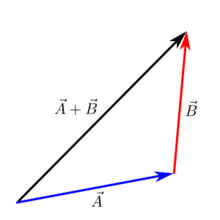
两个向量可以通过将第二个向量（此处为 **B**）的尾部与第一个向量（**A**）的尖端重合来图形化地相加。结果向量 **A** + **B** 是从 **A** 的尾部到 **B** 的尖端的向量。

任意数量的向量都可以通过这种方式相加。向量加法满足交换律

{\vec {A}}+{\vec {B}}+{\vec {C}}={\vec {C}}+{\vec {B}}+{\vec {A}}

和结合律

({\vec {A}}+{\vec {B}})+{\vec {C}}={\vec {A}}+({\vec {B}}+{\vec {C}})

点积

当我们乘以两个向量时，我们可以使用产生标量作为最终结果的乘法规则，也可以使用产生向量作为最终结果的乘法规则。产生标量的第一个规则称为 **点积**。在数学文本中，这通常称为 *内积*，一些较旧的文本将此称为 *标量积*（不要与标量乘法混淆）；它们都是一样的。点积具有乘积的所有通常性质，例如结合律、交换律和分配律。从几何上讲，点积定义为

{\vec {A}}\cdot {\vec {B}}=AB\cos(\theta )

,

其中 $\theta$ 是 ${\vec {A}}$ 和 ${\vec {B}}$ 之间的夹角。请注意，由于 $\cos(0)=1$ ，如果 ${\vec {A}}$ 平行于 ${\vec {B}}$ ，那么 ${\vec {A}}\cdot {\vec {B}}=AB$ 。另一方面，由于 $\cos(90^{\circ })=0$ 如果 ${\vec {A}}$ 垂直于 ${\vec {B}}$ ，那么 ${\vec {A}}\cdot {\vec {B}}=0$ 。利用这个指导原则，我们在下面找到关系

{\begin{aligned}{\hat {i}}\cdot {\hat {i}}={\hat {j}}\cdot {\hat {j}}={\hat {k}}\cdot {\hat {k}}=1\\{\hat {i}}\cdot {\hat {j}}={\hat {j}}\cdot {\hat {k}}={\hat {k}}\cdot {\hat {i}}=0\end{aligned}}

.

利用这一点，我们可以用分量向量来定义点积，如下所示

{\vec {A}}\cdot {\vec {B}}=(A_{x}~{\hat {i}}+A_{y}~{\hat {j}}+A_{z}~{\hat {k}})\cdot (B_{x}~{\hat {i}}+B_{y}~{\hat {j}}+B_{z}~{\hat {k}})=A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{z}

.

建议您明确展开乘法，使用分配律并找出哪些项消为零，哪些项变为 1。

叉积

两个向量相乘的第二条规则产生另一个向量。这个乘法规则非常特殊——事实上，它是三维空间的一个特殊属性，我们可以用这种方式定义向量乘法并仍然得到一个向量。这个规则在二维空间中不适用，而在任何超过三维的空间中，这个规则的扩展也不会产生另一个向量（例如，点积可以自然地扩展或限制到任何维度以产生一个标量）。这种乘法称为叉积，在其他文本中，你可能会发现术语外积和向量积。该积可以用两个规则来定义，首先指定乘积向量的方向，其次指定其大小。

${\vec {A}}\times {\vec {B}}$ 垂直于 ${\vec {A}}$ 和 ${\vec {B}}$ （即，垂直于这两个向量定义的平面）。这在垂直于平面的线上留下了两个可能的方向。这两个方向中的一个被称为“右手定则”：伸出食指、中指和大拇指，使它们相互垂直。让食指指向 ${\vec {A}}$ 的方向，中指指向 ${\vec {B}}$ 的方向。然后大拇指指向 ${\vec {A}}\times {\vec {B}}$ 的方向。这里顺序很重要（注意交换 A 和 B 会使大拇指指向相反的方向）。
$|{\vec {A}}\times {\vec {B}}|=AB\sin(\theta )$ ，其中 $\theta$ 再次是 ${\vec {A}}$ 和 ${\vec {B}}$ 之间的角度。

再次将此定义应用于单位向量，我们发现以下关系

{\begin{aligned}{\hat {i}}\times {\hat {j}}&=-{\hat {j}}\times {\hat {i}}={\hat {k}}\\{\hat {j}}\times {\hat {k}}&=-{\hat {k}}\times {\hat {j}}={\hat {i}}\\{\hat {k}}\times {\hat {i}}&=-{\hat {i}}\times {\hat {k}}={\hat {j}}\\{\hat {i}}\times {\hat {i}}&={\hat {j}}\times {\hat {j}}={\hat {k}}\times {\hat {k}}=0\end{aligned}}

.

而就分量而言，经过繁琐的代数运算，我们有

{\vec {A}}\times {\vec {B}}=(A_{y}B_{z}-B_{y}A_{z})~{\hat {i}}+(A_{z}B_{x}-B_{z}A_{x})~{\hat {j}}+(A_{x}B_{y}-B_{x}A_{y})~{\hat {k}}

.

事实证明，我们可以将这种复杂的关系写成一个 3×3 矩阵的行列式

{\vec {A}}\times {\vec {B}}=\left|{\begin{matrix}{\hat {i}}&{\hat {j}}&{\hat {k}}\\A_{x}&A_{y}&A_{z}\\B_{x}&B_{y}&B_{z}\end{matrix}}\right|

.

叉积的一些性质，比如 ${\vec {A}}\times {\vec {B}}=-{\vec {B}}\times {\vec {A}}$ 和 ${\vec {A}}\times {\vec {A}}=0$ 可以作为矩阵行列式的性质推导出来。

点积和叉积的有用性质

点积和叉积都对向量加法满足分配律。

${\vec {A}}\cdot ({\vec {B}}+{\vec {C}})={\vec {A}}\cdot {\vec {B}}+{\vec {A}}\cdot {\vec {C}}$

${\vec {A}}\times ({\vec {B}}+{\vec {C}})={\vec {A}}\times {\vec {B}}+{\vec {A}}\times {\vec {C}}$

$({\vec {A}}+{\vec {B}})\times {\vec {C}}={\vec {A}}\times {\vec {C}}+{\vec {B}}\times {\vec {C}}$

两个向量的点积与其夹角的余弦成正比，而其叉积与其夹角的正弦成正比。

${\vec {A}}\cdot {\vec {B}}=\|{\vec {A}}\|\|{\vec {B}}\|\cos(\theta )$

$\|{\vec {A}}\times {\vec {B}}\|=\|{\vec {A}}\|\|{\vec {B}}\|\sin(\theta )$

正如我们已经看到的，点积是结合律和交换律的。

${\vec {A}}\cdot ({\vec {B}}\cdot {\vec {C}})=({\vec {A}}\cdot {\vec {B}})\cdot {\vec {C}}$

${\vec {A}}\cdot {\vec {B}}={\vec {B}}\cdot {\vec {A}}$

重要的是要记住，叉积不具有这些性质。它不是交换律，而是反交换律。

${\vec {A}}\times {\vec {B}}=-{\vec {B}}\times {\vec {A}}$

叉积不具有结合律。例如，考虑 $({\vec {A}}\times {\vec {A}})\times {\vec {B}}$ 。因为 ${\vec {A}}$ 和它自身的夹角的正弦值为0，所以 ${\vec {A}}\times {\vec {A}}={\vec {0}}$ ，因此 $({\vec {A}}\times {\vec {A}})\times {\vec {B}}={\vec {0}}$ 。另一方面， ${\vec {A}}\times ({\vec {A}}\times {\vec {B}})$ 不为零，因为 ${\vec {A}}$ 和 ${\vec {A}}\times {\vec {B}}$ 是互相垂直的。实际上，如果 ${\vec {A}}$ 和 ${\vec {B}}$ 是互相垂直的，那么它的方向将与 ${\vec {B}}$ 的方向相反。您可以使用右手法则自己验证这一点。

${\vec {A}}$ 平行于 ${\vec {B}}$ 的分量由下式给出

$\left({\frac {{\vec {B}}\cdot {\vec {A}}}{{\vec {B}}\cdot {\vec {B}}}}\right){\vec {B}}$

而 ${\vec {A}}$ 垂直于 ${\vec {B}}$ 的分量由下式给出

$\left({\frac {{\vec {B}}\times {\vec {A}}}{{\vec {B}}\cdot {\vec {B}}}}\right)\times {\vec {B}}$ .

这导致了一些有趣的性质，涉及到乘积的组合，例如

$({\vec {B}}\cdot {\vec {B}}){\vec {A}}=({\vec {A}}\cdot {\vec {B}}){\vec {B}}+({\vec {B}}\times {\vec {A}})\times {\vec {B}}$ ,

${\vec {A}}\times ({\vec {B}}\times {\vec {C}})=({\vec {A}}\cdot {\vec {C}}){\vec {B}}-({\vec {A}}\cdot {\vec {B}}){\vec {C}}$ ，以及

$({\vec {A}}\times {\vec {B}})\cdot ({\vec {C}}\times {\vec {D}})=({\vec {A}}\cdot {\vec {C}})({\vec {B}}\cdot {\vec {D}})-({\vec {A}}\cdot {\vec {D}})({\vec {B}}\cdot {\vec {C}})$ .

链接

上一页：SI 单位制
顶部：测量
下一页：有效数字